Возможности нейронных сетей
Точное представление многочленов от многих переменных с помощью одного произвольного многочлена от одного переменного, линейных операций и суперпозиции
В этом разделе исследуются полугруппы полиномов от одного переменного относительно суперпозиции. Показано, что если такая полугруппа содержит все многочлены первой степени и хотя бы один - более высокой, то она включает все многочлены. На основании этого факта доказано, что всегда возможно представить многочлен от многих переменных суперпозициями произвольного нелинейного многочлена от одного переменного и линейных функций.
Вернемся к классическому вопросу о представлении функций многих переменных с помощью функций меньшего числа переменных. Следует еще раз заметить, что классических вопроса существует не один, а два:
- Можно ли получить точное представление функции многих переменных с помощью суперпозиции функций меньшего числа переменных?
- Можно ли получить сколь угодно точную аппроксимацию функции многих переменных с помощью некоторых более простых функций и операций?
В рамках первого вопроса особый интерес представляют конструкции, в которых для точного представления всех функций многих переменных используется один и тот же набор функций одного переменного.
Традиционно считается, что эти функции должны иметь весьма специальный и довольно экзотический вид, например, как в обсуждавшейся выше теореме Колмогорова, где использовались существенно негладкие функции.
Напротив, свобода в выборе функций одного переменного для решения второго вопроса при том же самоограничении (один набор функций одного переменного - для приближенного представления всех функций многих переменных) очень велика. Для этого, как показано в предыдущем разделе, можно использовать практически любую нелинейную функцию и достаточно всего одной.
Далее доказываются теоремы, относящиеся к первому вопросу (точное представление). В частности, показано, что можно точно представить любой многочлен от многих переменных с помощью суперпозиций произвольного нелинейного многочлена от одного переменного и линейных функций. Следовательно особенной пропасти между 1-м и 2-м вопросом не существует. Именно это обстоятельство побудило нас включить в книгу данный раздел.
Пусть R[X] - кольцо многочленов от одного переменного над полем R, ![{\rm{E}} \subset {\rm{R[X]}}](/sites/default/files/tex_cache/5539a0c2a650d775062e1d4b2ac03c07.png)
- линейное пространство многочленов над R.
Предложение 1. Если E замкнуто относительно суперпозиции многочленов, содержит все многочлены первой степени и хотя бы один многочлен p(x) степени m>1, то E=R[X].
Доказательство. Заметим, что степень многочлена p'(x)=p(x+1)-p(x) равна m-1, и 
, так как E содержит многочлены первой степени (поэтому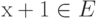 
), замкнуто относительно суперпозиции (поэтому 
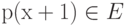) и линейных операций (поэтому ).
Если m>2, то понижаем степень с помощью конечных разностей (переходим к p', p'' и т.д.), пока не получим многочлен второй степени. Вычитая из него линейную часть и умножая на константу, получаем: 
. Поэтому для любого 
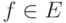имеем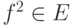 
(т.к. E - полугруппа). Дальнейшее очевидно: как неоднократно отмечалось выше, отсюда следует, что для любых 
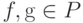их произведение 
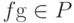а с помощью умножения и сложения многочленов первой степени порождается все кольцо R[X].
Перейдем к задаче представления многочленов от многих переменных. Обозначим R[X1, ..., Xn] кольцо многочленов от n переменных над полем R.
Для каждого многочлена от одного переменного введем множество тех многочленов, которые можно выразить с его помощью, используя суперпозиции и линейные функции. Пусть p - многочлен от одного переменного, Ep[X1, ..., Xn] - множество многочленов от n переменных, которое можно получить из p и многочленов первой степени, принадлежащих R[X1, ..., Xn], с помощью операций суперпозиции, сложения и умножения на число.
Следующие два предложения дают удобную для дальнейшего характеризацию Ep[X1, ..., Xn] и следуют непосредственно из определений.
Предложение 2. Множество Ep[X1, ..., Xn] является линейным пространством над R и для любого многочлена g(x1, ... ,xn) из ![{\rm{E}}_{\rm{p}}{\rm{[X}}_{\rm{1}}{\rm{, }}...,{\rm{X}}_{\rm{n}}{\rm{] p(g(x}}_{\rm{1}}{\rm{, }}...{\rm{,x}}_{\rm{n}})) \in {\rm{E}}_{\rm{p}}{\rm{[X}}_{\rm{1}}{\rm{, }}...,{\rm{X}}_{\rm{n}}{\rm{]}}](/sites/default/files/tex_cache/f22fcb6a922373bda3378f5362444099.png)
.
Предложение 3. Для данного p семейство линейных подпространств ![{\rm{L}} \subseteq {\rm{R[X}}_{\rm{1}}{\rm{, }}...,{\rm{X}}_{\rm{n}}{\rm{]}}](/sites/default/files/tex_cache/7b4ba1c6cac4accebfbb9a892ab04a24.png)
, содержащих все многочлены первой степени и удовлетворяющих условию
если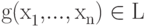 
, то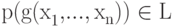 
,
замкнуто относительно пересечений. Минимальным по включению элементом этого семейства является Ep[X1, ..., Xn].
Для любого линейного подпространства ![{\rm{E}} \subseteq {\rm{R[X}}_{\rm{1}}{\rm{, }}...,{\rm{X}}_{\rm{n}}{\rm{]}}](/sites/default/files/tex_cache/cbe2e7a17b508c0b4720ddeee5085300.png)
рассмотрим множество алгебраических унарных операций, которые переводят элементы E в элементы E:
![{\rm{P}}_{\rm{E}}{\rm{=\{p}} \in {\rm{R[X]|p(g(x}}_{\rm{1}}{\rm{, }}...{\rm{,x}}_{\rm{n}}{\rm{))}} \in {\rm{E}}](/sites/default/files/tex_cache/d268f03691a9ebcc4f5b8db3261ebb93.png)
для любого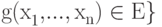 
.
Предложение 4. Для любого линейного подпространства множество полиномов PE является линейным пространством над R, замкнуто относительно суперпозиции и содержит все однородные многочлены первой степени.
Если линейное пространство E содержит 1, а PE включает хотя бы один многочлен, степени m>1 (т.е. нелинейный), то PE=R[X].
Доказательство. Замкнутость PE относительно суперпозиции следует из определения, все однородные полиномы первой степени входят в PE, поскольку E является линейным пространством, отсюда также следует, что PE является линейным пространством. Наконец, если 
и PE содержит многочлен степени m>1, то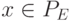 
, тогда PE=R[X] по предложению 1.
Теорема 3. Пусть - линейное подпространство, PE содержит хотя бы один многочлен степени m>1 и , тогда E является кольцом (с единицей).
Доказательство. По предложению 4 в условиях теоремы PE=R[X]. В частности,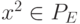 
. Это означает, что для любого 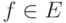также и 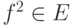. Поэтому для любых 
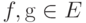получаем: 
.
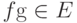Теорема 4. Для любого многочлена p степени m>1
Ep[X1, ..., Xn]=R[X1, ..., Xn]
Доказательство. Заметим, что E=Ep[X1, ..., Xn] - линейное подпространство в R[X1, ..., Xn], PE содержит хотя бы один многочлен ( p ) степени m>1 и E содержит все многочлены первой степени (и поэтому также 1 ). В силу теоремы 3, E является кольцом, а так как оно содержит все многочлены первой степени, то совпадает с R[X1, ..., Xn], поскольку, используя умножение и сложение можно из этих многочленов получить любой.
Таким образом, из p и многочленов первой степени с помощью операций суперпозиции, сложения и умножения на число можно получить все элементы R[X1, ..., Xn].