Возможности нейронных сетей
Теорема 2. Пусть множество 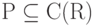 удовлетворяет условиям 1-4. Тогда P=C(R).
удовлетворяет условиям 1-4. Тогда P=C(R).
Доказательство опирается на три леммы.
Лемма 1. В условиях теоремы 2 существует дважды непрерывно дифференцируемая функция 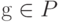 , не являющаяся линейной.
, не являющаяся линейной.
Доказательство. Пусть  , v(x)=0 при |x|>1,
, v(x)=0 при |x|>1,  . Рассмотрим оператор осреднения
. Рассмотрим оператор осреднения
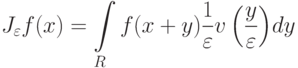
Для любого 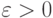 выполнено:
выполнено: 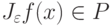 .
.
Действительно,  для каждого фиксированного y ((т.к. константы принадлежат E и E замкнуто относительно линейных операций и суперпозиции функций). Интеграл
для каждого фиксированного y ((т.к. константы принадлежат E и E замкнуто относительно линейных операций и суперпозиции функций). Интеграл 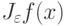 . принадлежит E, так как E является замкнутым линейным подпространством в C(R), а этот интеграл пределом конечных сумм.
. принадлежит E, так как E является замкнутым линейным подпространством в C(R), а этот интеграл пределом конечных сумм.
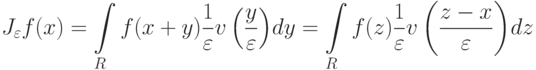
(напомним, что v – функция с компактным носителем).
Существует такое 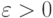 , что функция
, что функция  не является линейной, поскольку
не является линейной, поскольку  не является линейной, поскольку
не является линейной, поскольку 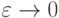 , пространство линейных функций замкнуто, а f не является линейной функцией. Таким образом, в предположениях леммы существует нелинейная функция
, пространство линейных функций замкнуто, а f не является линейной функцией. Таким образом, в предположениях леммы существует нелинейная функция 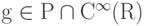 , которую можно выбрать в виде
, которую можно выбрать в виде 
Лемма 2. Пусть в условиях теоремы 2 существует дважды непрерывно дифференцируемая функция 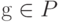 , не являющаяся линейной. Тогда функция q(x)=x2 принадлежит P.
, не являющаяся линейной. Тогда функция q(x)=x2 принадлежит P.
Доказательство. Существует точка x0, для которой 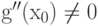 . Обозначим r(x)=2(g(x+x0)-g(x0)-xg'(x0))/g''(x0). Очевидно, что
. Обозначим r(x)=2(g(x+x0)-g(x0)-xg'(x0))/g''(x0). Очевидно, что 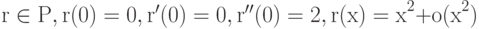 . Поэтому
. Поэтому
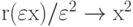 при
при 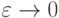 .
.
Поскольку P замкнуто, получаем: функция q(x)=x2 принадлежит P.
Лемма 3. Пусть в условиях теоремы 2 функция q(x)=x2 принадлежит P. Тогда P является кольцом - для любых 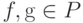 их произведение
их произведение 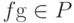 .
.
Доказательство. Действительно, ![fg=\frac{1}{2}\left[{(f+g)^2 - f^2 - g^2}\right]](/sites/default/files/tex_cache/9e473911c1b753bf55fcd9488cf2f630.png) и, так как P замкнуто относительно суперпозиции и линейных операций, то
и, так как P замкнуто относительно суперпозиции и линейных операций, то 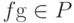 .
.
Доказательство теоремы 2 заканчивается обращением к классической теореме Вейерштрасса о приближении функций многочленами: из лемм 1-3 следует, что в условиях теоремы 2 P является кольцом и, в частности, содержит все многочлены (которые получаются из 1 и id с помощью умножения и линейных операций). По теореме Вейерштрасса отсюда следует, что P=C(R) .
Теоремы 1,2 можно трактовать как утверждения о универсальных аппроксимационных свойствах любой нелинейности: с помощью линейных операций и каскадного соединения можно из произвольных нелинейных элементов получить любой требуемый результат с любой наперед заданной точностью.

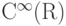 так как
так как