Возможности нейронных сетей

Универсальные аппроксимационные способности произвольной нелинейности и обобщенная теорема Стоуна

В этом разделе для множеств непрерывных функций, замкнутых относительно любой нелинейной операции (а не только для колец), доказана обобщенная аппроксимационная теорема Стоуна. Это интерпретируется как утверждение о универсальных аппроксимационных возможностях произвольной нелинейности: с помощью линейных операций и каскадного соединения можно из произвольного нелинейного элемента получить устройство, вычисляющее любую непрерывную функцию с любой наперед заданной точностью.

Рассмотрим компактное пространство X и алгебру C(X) непрерывных функций на X с вещественными значениями.

Кроме аппроксимации функций многочленами и их обобщениями из колец функций, разделяющих точки, в последнее время все большее внимание уделяется приближению функций многих переменных с помощью линейных операций и суперпозиций функций одного переменного. Такое приближение осуществляется специальными формальными "устройствами" - нейронными сетями. Каждая сеть состоит из формальных нейронов. Нейрон получает на входе вектор сигналов x, вычисляет его скалярное произведение на вектор весов a и некоторую функцию одного переменного 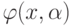. Результат рассылается на входы других нейронов или передается на выход. Таким образом, нейронные сети вычисляют суперпозиции простых функций одного переменного и их линейных комбинаций.

Доказан ряд теорем [1.8, 1.9, 1.10] об аппроксимации непрерывных функций многих переменных нейронными сетями с использованием практически произвольной непрерывной функции одного переменного. В данном разделе мы покажем, что эта функция действительно может быть произвольной и докажем обобщенную теорему Стоуна, естественным образом охватывающую и классическую теорему Стоуна, и аппроксимацию функций многих переменных суперпозициями и линейными комбинациями функций одного переменного.

Чтобы получить требуемое обобщение, перейдем от рассмотрения колец функций к изучению их алгебр, замкнутых относительно некоторой нелинейной унарной операции.

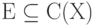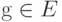Пусть - линейное пространство, C(R) - пространство непрерывных функций на действительной оси R, - нелинейная функция и для любого выполнено . В этом случае будем говорить, что E замкнуто относительно нелинейной унарной операции f.

Очевидный пример: множество функций n переменных, которые можно точно представить, используя заданную функцию одного переменного и линейные функции, является линейным пространством, замкнутым относительно нелинейной унарной операции f.

Замечание. Линейное пространство 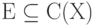замкнуто относительно нелинейной операции f(x)=x² тогда и только тогда, когда E является кольцом.

Действительно, поэтому для линейного пространства 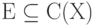замкнутость относительно унарной операции f(x)=x² равносильна замкнутости относительно произведения функций.

Согласно приведенному замечанию, теорема Стоуна может быть переформулирована так.

Пусть 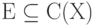- замкнутое линейное подпространство в C(X), , функции из E разделяют точки в X и E замкнуто относительно нелинейной унарной операции f(x)=x². Тогда E=C(X) .

Наше обобщение теоремы Стоуна состоит в замене f(x)=x² на произвольную нелинейную непрерывную функцию.

Теорема 1. Пусть 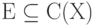- замкнутое линейное подпространство в C(X), , функции из E разделяют точки в X и E замкнуто относительно нелинейной унарной операции 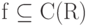. Тогда E=C(X) .

Доказательство. Рассмотрим множество всех таких 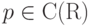, что 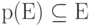, то есть для любого 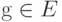выполнено: . Обозначим это множество P_E. Оно обладает следующими свойствами:

1. P_E - полугруппа относительно суперпозиции функций;
2. P_E - замкнутое линейное подпространство в C(R) (в топологии равномерной сходимости на компактах);
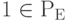3. и .
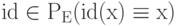4. P_E включает хоть одну непрерывную нелинейную функцию.

Дальнейшее следует из теоремы 2, которая является, по существу, подготовительной теоремой о полугруппах функций.