Параллельные методы сортировки
9.5.4. Сортировка с использованием регулярного набора образцов
9.5.4.1. Организация параллельных вычислений
Алгоритм сортировки с использованием регулярного набора образцов ( the parallel sorting by regular sampling ) также является обобщением метода быстрой сортировки (см., например, в [ [ 63 ] ]).
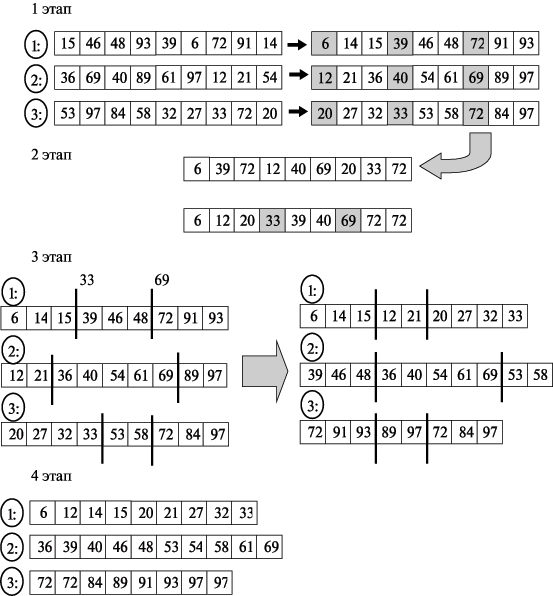
Упорядочивание данных в соответствии с данным вариантом алгоритма быстрой сортировки осуществляется в ходе выполнения следующих четырех этапов:
- на первом этапе сортировки производится упорядочивание имеющихся на процессорах блоков. Данная операция может быть выполнена каждым процессором независимо друг от друга при помощи обычного алгоритма быстрой сортировки ; далее каждый процессор формирует набор из элементов своих блоков с индексами 0, m, 2m, ...,(p-1)m, где m=n/p2 ;
- на втором этапе выполнения алгоритма
все сформированные на процессорах наборы данных собираются на
одном из процессоров системы и объединяются в ходе
последовательного слияния в одно упорядоченное множество. Далее
из полученного множества значений из элементов с индексамиформируется новый набор ведущих элементов, который передается всем используемым процессорам. В завершение этапа каждый процессор выполняет разделение своего блока на p частей с использованием полученного набора ведущих значений;

- на третьем этапе сортировки каждый процессор осуществляет рассылку выделенных ранее частей своего блока всем остальным процессорам системы; рассылка выполняется в соответствии с порядком нумерации – часть j, 0<=j<p, каждого блока пересылается процессору с номером j ;
- на четвертом этапе выполнения алгоритма каждый процессор выполняет слияние p полученных частей в один отсортированный блок.
По завершении четвертого этапа исходный набор данных становится отсортированным.
На рис. 9.11 приведен пример сортировки массива данных с помощью алгоритма, описанного выше. Следует отметить, что число процессоров для данного алгоритма может быть произвольным, в данном примере оно равно 3.
9.5.4.2. Анализ эффективности
Оценим трудоемкость рассмотренного параллельного метода. Пусть, как и ранее, n есть количество сортируемых данных, p, p<n, обозначает число используемых процессоров и, соответственно, n/p есть размер блоков данных на процессорах.
В течение первого этапа алгоритма каждый процессор сортирует свой блок данных с помощью быстрой сортировки, тем самым, длительность выполняемых при этом операций равна
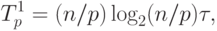 |
( 9.13) |
 есть время выполнения базовой операции сортировки.
есть время выполнения базовой операции сортировки.На втором этапе алгоритма один из процессоров собирает наборы из p элементов со всех остальных процессоров, выполняет слияние всех полученных данных (общее количество элементов составляет p2 ), формирует набор из p-1 ведущих элементов и рассылает полученный набор всем остальным процессорам. С учетом всех перечисленных действий общая длительность второго этапа составляет
![T_p^2=[\alpha\log_2p+wp(p-1)/ \beta]+
[p^2\log_2p\tau]+[p\tau]+
[\log_2p(\alpha+wp/ \beta)]](/sites/default/files/tex_cache/c376b2e6af448fcf3d4a4c1d38f83839.png) |
( 9.14) |
 – латентность,
– латентность,  – пропускная способность сети
передачи данных, а w есть размер элемента
упорядочиваемых данных в байтах.
– пропускная способность сети
передачи данных, а w есть размер элемента
упорядочиваемых данных в байтах.В ходе выполнения третьего этапа алгоритма каждый процессор разделяет свои элементы относительно ведущих элементов на p частей (общее количество операций для этого может быть ограничено величиной n/p ). Далее все процессоры выполняют рассылку сформированных частей блоков между собой – оценка трудоемкости такой коммуникационной операции рассмотрена в "Оценка коммуникационной трудоемкости параллельных алгоритмов" при представлении топологии вычислительной сети в виде гиперкуба. Как было показано, выполнение такой операции может быть осуществлено за log2p шагов, на каждом из которых каждый процессор передает и получает сообщение из (n/p)/2 элементов. Как результат, общая трудоемкость третьего этапа алгоритма может быть оценена как
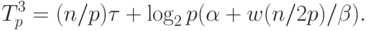 |
( 9.15) |
На четвертом этапе алгоритма каждый процессор выполняет слияние p отсортированных частей в один объединенный блок. Оценка трудоемкости такой операции уже проводилась при рассмотрении второго этапа, и, тем самым, длительность выполнения процедуры слияния составляет
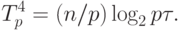 |
( 9.16) |
С учетом всех полученных соотношений общее время выполнения алгоритма сортировки с использованием регулярного набора образцов составляет
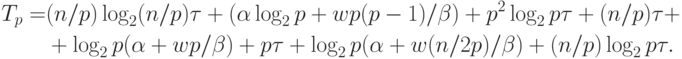 |
( 9.17) |
9.5.4.3. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта сортировки с использованием регулярного набора образцов осуществлялись при тех же условиях, что и ранее выполненные (см. п. 9.3.6).
Результаты вычислительных экспериментов даны в табл. 9.10. Эксперименты проводились с использованием двух и четырех процессоров. Время указано в секундах.
| Количество элементов | Последовательный алгоритм | Параллельный алгоритм | |||
|---|---|---|---|---|---|
| 2 процессора | 4 процессора | ||||
| Время | Ускорение | Время | Ускорение | ||
| 10000 | 0,001422 | 0,001513 | 0,939855 | 0,001166 | 1,219554 |
| 20000 | 0,002991 | 0,002307 | 1,396489 | 0,002081 | 1,437290 |
| 30000 | 0,004612 | 0,003168 | 1,455808 | 0,003099 | 1,488222 |
| 40000 | 0,006297 | 0,004542 | 1,386394 | 0,003819 | 1,648861 |
| 50000 | 0,008014 | 0,005503 | 1,456297 | 0,004370 | 1,833867 |
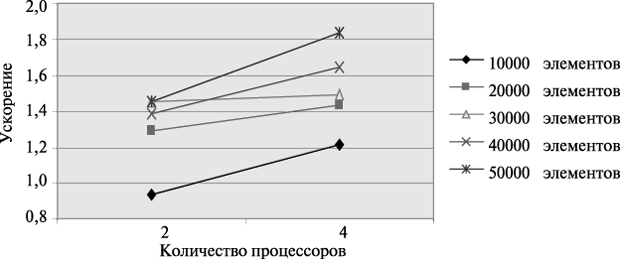
Рис. 9.12. Зависимость ускорения от количества процессоров при выполнении параллельного алгоритма сортировки с использованием регулярного набора образцов
| Количество элементов | Параллельный алгоритм | |||
|---|---|---|---|---|
| 2 процессора | 4 процессора | |||
 |
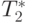 |
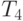 |
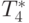 |
|
| 10000 | 0,001533 | 0,001513 | 0,001762 | 0,001166 |
| 20000 | 0,002569 | 0,002307 | 0,002375 | 0,002081 |
| 30000 | 0,003645 | 0,003168 | 0,003007 | 0,003099 |
| 40000 | 0,004747 | 0,004542 | 0,003652 | 0,003819 |
| 50000 | 0,005867 | 0,005503 | 0,004307 | 0,004370 |
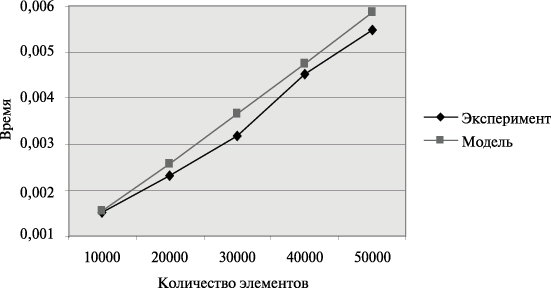
Сравнение времени выполнения эксперимента 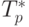 и
теоретической оценки Tp из (9.17)
приведено в таблице 9.11 и на
рис. 9.13.
и
теоретической оценки Tp из (9.17)
приведено в таблице 9.11 и на
рис. 9.13.