Параллельные методы сортировки
9.4. Сортировка Шелла
9.4.1. Последовательный алгоритм
Общая идея сортировки Шелла ( the Shell sort ) (см., например, [26, 50]) состоит в сравнении на начальных стадиях сортировки пар значений, располагаемых достаточно далеко друг от друга в упорядочиваемом наборе данных. Такая модификация метода сортировки позволяет быстро переставлять далекие неупорядоченные пары значений ( сортировка таких пар обычно требует большого количества перестановок, если используется сравнение только соседних элементов).
Общая схема метода состоит в следующем. На первом шаге алгоритма происходит упорядочивание элементов n/2 пар (ai, an/2+i) для 1<=i<=n/2. Далее, на втором шаге упорядочиваются элементы в n/4 группах из четырех элементов (ai, an/4+i, an/2+i, a3n/4+i) для 1<=i<=n/4. На третьем шаге упорядочиваются элементы уже в n/8 группах из восьми элементов и т.д. На последнем шаге упорядочиваются элементы сразу во всем массиве (a1, a2, ..., an). На каждом шаге для упорядочивания элементов в группах применяется метод сортировки вставками. Как можно заметить, общее количество итераций алгоритма Шелла равно log2n.
В более полном виде алгоритм Шелла может быть представлен следующим образом.
Алгоритм 9.4. Последовательный алгоритм сортировки Шелла
// Алгоритм 9.4
// Последовательный алгоритм сортировки Шелла
void ShellSort(double A[], int n) {
int incr = n / 2;
while (incr > 0) {
for (int i = incr + 1; i < n; i++) {
int j = i - incr;
while (j > 0)
if (A[j] > A[j + incr]) {
swap(A[j], A[j + incr]);
j = j - incr;
}
else j = 0;
}
incr = incr/2;
}
}9.4.2. Организация параллельных вычислений
Для алгоритма Шелла может быть предложен параллельный аналог метода (см., например, [ [ 51 ] ]), если топология коммуникационной сети может быть эффективно представлена в виде N -мерного гиперкуба (т. е. количество процессоров равно p = 2N ). Выполнение сортировки в таком случае может быть разделено на два последовательных этапа. На первом этапе ( N итераций) осуществляется взаимодействие процессоров, являющихся соседними в структуре гиперкуба (но эти процессоры могут оказаться далекими при линейной нумерации; для установления соответствия двух систем нумерации процессоров может быть использован, как и ранее, код Грея – см. "Оценка коммуникационной трудоемкости параллельных алгоритмов" ). Формирование пар процессоров, взаимодействующих между собой при выполнении операции "сравнить и разделить", может быть обеспечено при помощи следующего простого правила – на каждой итерации i, 0<=i<N, парными становятся процессоры, у которых различие в битовых представлениях их номеров имеется только в позиции N-i.
Второй этап состоит в реализации обычных итераций параллельного алгоритма чет-нечетной перестановки. Итерации данного этапа выполняются до прекращения фактического изменения сортируемого набора, и, тем самым, общее количество L таких итераций может быть различным – от 2 до p.
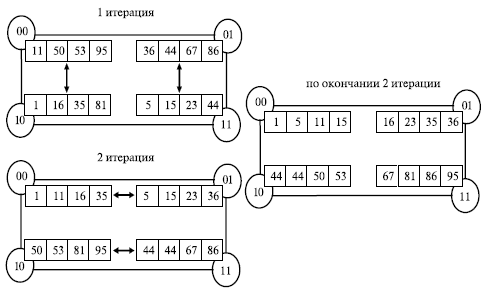
На рис. 9.3 показан пример сортировки массива из 16 элементов с помощью рассмотренного способа (процессоры показаны кружками, номера процессоров даны в битовом представлении). Нужно заметить, что данные оказываются упорядоченными уже после первого этапа и нет необходимости выполнять чет-нечетную перестановку.
С учетом представленного описания параллельного варианта алгоритма Шелла базовая подзадача для организации параллельных вычислений, как и ранее (см. п. 9.3.3), может быть определена на основе операции "сравнить и разделить". Как результат, количество подзадач всегда совпадает с числом имеющихся процессоров (размер блоков данных в подзадачах равен n/p) и не возникает проблемы масштабирования. Распределение блоков упорядочиваемого набора данных по процессорам должно быть выбрано с учетом возможности эффективного выполнения операций "сравнить и разделить" при представлении топологии сети передачи данных в виде гиперкуба.
9.4.3. Анализ эффективности
Для оценки эффективности параллельного аналога алгоритма Шелла могут быть использованы соотношения, полученные для параллельного метода пузырьковой сортировки (см. п. 9.3.5). При этом следует только учесть двухэтапность алгоритма Шелла – с учетом данной особенности общее время выполнения нового параллельного метода может быть определено при помощи выражения
![T_p=(n/p)\log_2(n/p)\tau+(\log_2 p+L)[(2n/p)\tau+(\alpha+w\cdot(n/p)/ \beta)]](/sites/default/files/tex_cache/975c8c1286c884836e9e54d8a5f7dba4.png) |
( 9.7) |
Как можно заметить, эффективность параллельного варианта сортировки Шелла существенно зависит от значения L – при малом значении величины L новый параллельный способ сортировки выполняется быстрее, чем ранее рассмотренный алгоритм чет-нечетной перестановки.
9.4.4. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта сортировки Шелла осуществлялись при тех же условиях, что и ранее выполненные (см. п. 9.3.6).
Результаты вычислительных экспериментов приведены в табл. 9.4. Эксперименты проводились с использованием двух и четырех процессоров. Время указано в секундах.
| Количество элементов | Последовательный алгоритм | Параллельный алгоритм | |||
|---|---|---|---|---|---|
| 2 процессора | 4 процессора | ||||
| Время | Ускорение | Время | Ускорение | ||
| 10000 | 0,001422 | 0,002959 | 0,480568 | 0,007509 | 0,189373 |
| 20000 | 0,002991 | 0,004557 | 0,656353 | 0,009826 | 0,304396 |
| 30000 | 0,004612 | 0,006118 | 0,753841 | 0,012431 | 0,371008 |
| 40000 | 0,006297 | 0,008461 | 0,744238 | 0,017009 | 0,370216 |
| 50000 | 0,008014 | 0,009920 | 0,807863 | 0,019419 | 0,412689 |
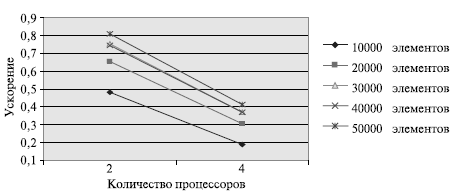
Рис. 9.4. Зависимость ускорения от количества процессоров при выполнении параллельного алгоритма сортировки Шелла
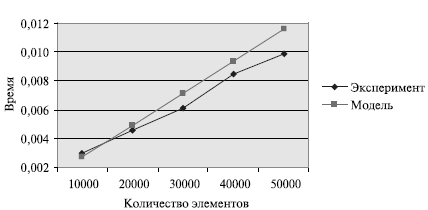
Сравнение времени выполнения эксперимента 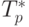 и теоретической
оценки Tp из (9.7) приведено в таблице 9.5 и на рис. 9.5.
и теоретической
оценки Tp из (9.7) приведено в таблице 9.5 и на рис. 9.5.
| Количество элементов | Параллельный алгоритм | |||
|---|---|---|---|---|
| 2 процессора | 4 процессора | |||
 |
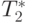 |
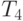 |
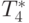 |
|
| 1000 | 0,002684 | 0,002959 | 0,002938 | 0,007509 |
| 20000 | 0,004872 | 0,004557 | 0,004729 | 0,009826 |
| 30000 | 0,007100 | 0,006118 | 0,006538 | 0,012431 |
| 40000 | 0,009353 | 0,008461 | 0,008361 | 0,017009 |
| 50000 | 0,011625 | 0,009920 | 0,010193 | 0,019419 |