НОУ ИНТУИТ | Теория и практика параллельных вычислений. Лекция 9: Параллельные методы сортировки

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.07.2007 | Доступ: свободный | Студентов: 2035 / 507 | Оценка: 4.53 / 4.26 | Длительность: 25:10:00

ISBN: 978-5-9556-0096-3

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

9.3. Пузырьковая сортировка

9.3.1. Последовательный алгоритм

Последовательный алгоритм пузырьковой сортировки ( the bubble sort algorithm ) (см., например, [ [ 26 ] , [ 50 ] ]) сравнивает и обменивает соседние элементы в последовательности, которую нужно отсортировать. Для последовательности

(a₁, a₂, ..., a_n)

алгоритм сначала выполняет n-1 базовых операций "сравнения-обмена" для последовательных пар элементов

(a₁, a₂), (a₂, a₃), ..., (a_n-1, a_n).

В результате после первой итерации алгоритма самый большой элемент перемещается ("всплывает") в конец последовательности. Далее последний элемент в преобразованной последовательности может быть исключен из рассмотрения, и описанная выше процедура применяется к оставшейся части последовательности

(a'₁, a'₂, ..., a'_n-1).

Как можно увидеть, последовательность будет отсортирована после n-1 итерации. Эффективность пузырьковой сортировки может быть улучшена, если завершать алгоритм в случае отсутствия каких- либо изменений сортируемой последовательности данных в ходе какой-либо итерации сортировки.

Алгоритм 9.1. Последовательный алгоритм пузырьковой сортировки

// Алгоритм 9.1.
// Последовательный алгоритм пузырьковой сортировки
void BubbleSort(double A[], int n) {
  for (int i = 0; i < n - 1; i++) 
    for (int j = 0; j < n - i; j++)
      compare_exchange(A[j], A[j + 1]);
}

9.3.2. Алгоритм чет-нечетной перестановки

Алгоритм пузырьковой сортировки в прямом виде достаточно сложен для распараллеливания – сравнение пар значений упорядочиваемого набора данных происходит строго последовательно. В связи с этим для параллельного применения используется не сам этот алгоритм, а его модификация, известная в литературе как метод чет-нечетной перестановки ( the odd-even transposition method ) – см., например, [ [ 51 ] ]. Суть модификации состоит в том, что в алгоритм сортировки вводятся два разных правила выполнения итераций метода: в зависимости от четности или нечетности номера итерации сортировки для обработки выбираются элементы с четными или нечетными индексами соответственно, сравнение выделяемых значений всегда осуществляется с их правыми соседними элементами. Таким образом, на всех нечетных итерациях сравниваются пары

(a₁, a₂), (a₃, a₄), ..., (a_n-1,a_n) (при четном n),

а на четных итерациях обрабатываются элементы

(a₂, a₃), (a₄, a₅), ..., (a_n-2,a_n-1).

После n -кратного повторения итераций сортировки исходный набор данных оказывается упорядоченным.

Алгоритм 9.2. Последовательный алгоритм чет-нечетной перестановки

// Алгоритм 9.2
// Последовательный алгоритм чет-нечетной перестановки
void OddEvenSort(double A[], int n) {
  for (int i = 1; i < n; i++) {
    if (i % 2 == 1) {    // нечетная итерация
      for (int j = 0; j < n/2 - 2; j++) 
        compare_exchange(A[2*j + 1], A[2*j + 2]);
      if (n % 2 == 1) // сравнение последней пары при нечетном n
        compare_exchange(A[n - 2], A[n - 1]);
     }
     else    // четная итерация
       for (int j = 1; j < n/2 - 1; j++) 
         compare_exchange(A[2*j], A[2*j + 1]);
  }
}

9.3.3. Определение подзадач и выделение информационных зависимостей

Получение параллельного варианта для метода чет-нечетной перестановки уже не представляет каких-либо затруднений – сравнения пар значений на итерациях сортировки являются независимыми и могут быть выполнены параллельно. В случае p<n, когда количество процессоров меньше числа упорядочиваемых значений, процессоры содержат блоки данных размера n/p и в качестве базовой подзадачи может быть использована операция "сравнить и разделить" (см. подраздел 9.2).

Алгоритм 9.3. Параллельный алгоритм чет-нечетной перестановки

// Алгоритм 9.3
// Параллельный алгоритм чет-нечетной перестановки
ParallelOddEvenSort(double A[], int n) {
  int id = GetProcId();     // номер процесса 
  int np = GetProcNum();    // количество процессов 
  for (int i = 0; i < np; i++ ) {
    if (i % 2 == 1) {    // нечетная итерация
      if (id % 2 == 1) {    // нечетный номер процесса
        // Cравнение-обмен с процессом — соседом справа
        if (id < np - 1) compare_split_min(id + 1);
      }
      else
        // Cравнение-обмен с процессом — соседом слева
        if (id > 0) compare_split_max(id - 1);
    }
    else {    // четная итерация
      if(id % 2 == 0) {    // четный номер процесса
        // Cравнение-обмен с процессом — соседом справа
        if (id < np - 1) compare_split_min(id + 1);
      }
      else
        // Cравнение-обмен с процессом — соседом слева
        compare_split_max(id - 1);
    }
  }
}

Для пояснения такого параллельного способа сортировки в табл. 9.1 приведен пример упорядочения данных при n=16, p=4 (т.е. блок значений на каждом процессоре содержит n/p=4 элемента). В первом столбце таблицы приводится номер и тип итерации метода, перечисляются пары процессов, для которых параллельно выполняются операции "сравнить и разделить". Взаимодействующие пары процессов выделены в таблице рамкой. Для каждого шага сортировки показано состояние упорядочиваемого набора данных до и после выполнения итерации.

В общем случае выполнение параллельного метода может быть прекращено, если в течение каких-либо двух последовательных итераций сортировки состояние упорядочиваемого набора данных не было изменено. Как результат, общее количество итераций может быть сокращено, и для фиксации таких моментов необходимо введение некоторого управляющего процессора, который определял бы состояние набора данных после выполнения каждой итерации сортировки. Однако трудоемкость такой коммуникационной операции (сборка на одном процессоре сообщений от всех процессоров) может оказаться столь значительной, что весь эффект от возможного сокращения итераций сортировки будет поглощен затратами на реализацию операций межпроцессорной передачи данных.

Таблица 9.1. Пример сортировки данных параллельным методом чет-нечетной перестановки
№ и тип итераци	Процессоры
№ и тип итераци	1	2	3	4
Исходные данные	13 55 59 88	29 43 71 85	2 18 40 75	4 14 22 43
1 нечет (1, 2), (3, 4)	13 55 59 88	29 43 71 85	2 18 40 75	4 14 22 43
1 нечет (1, 2), (3, 4)	13 29 43 55	59 71 85 88	2 4 14 18	22 40 43 75
2 чет (2, 3)	13 29 43 55	59 71 85 88	2 4 14 18	22 40 43 75
2 чет (2, 3)	13 29 43 55	2 4 14 18	59 71 85 88	22 40 43 75
3 нечет (1, 2), (3, 4)	13 29 43 55	2 4 14 18	59 71 85 88	22 40 43 75
3 нечет (1, 2), (3, 4)	2 4 13 14	18 29 43 55	22 40 43 59	71 75 85 88
4 чет (2, 3)	2 4 13 14	18 29 43 55	22 40 43 59	71 75 85 88
4 чет (2, 3)	2 4 13 14	18 22 29 40	43 43 55 59	71 75 85 88

9.3.4. Масштабирование и распределение подзадач по процессорам

Как отмечалось ранее, количество подзадач соответствует числу имеющихся процессоров, и поэтому необходимости в проведении масштабирования вычислений не возникает. Исходное распределение блоков упорядочиваемого набора данных по процессорам может быть выбрано совершенно произвольным образом. Для эффективного выполнения рассмотренного параллельного алгоритма сортировки нужно, чтобы процессоры с соседними номерами имели прямые линии связи.

9.3.5. Анализ эффективности

При анализе эффективности, как и ранее, вначале проведем общую оценку сложности рассмотренного параллельного алгоритма сортировки, а затем дополним полученные соотношения показателями трудоемкости выполняемых коммуникационных операций.

Определим первоначально трудоемкость последовательных вычислений. При рассмотрении данного вопроса алгоритм пузырьковой сортировки позволяет продемонстрировать следующий важный момент. Как уже отмечалось в начале этой лекции, использованный для распараллеливания последовательный метод упорядочивания данных характеризуется квадратичной зависимостью сложности от числа упорядочиваемых данных, т.е. T₁~n². Однако применение подобной оценки сложности последовательного алгоритма приведет к искажению исходного целевого назначения критериев качества параллельных вычислений – показатели эффективности в этом случае будут характеризовать используемый способ параллельного выполнения данного конкретного метода сортировки, а не результативность использования параллелизма для задачи упорядочивания данных в целом как таковой. Различие состоит в том, что для сортировки могут быть применены более эффективные последовательные алгоритмы, трудоемкость которых имеет порядок

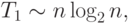$T_1 \sim n \log_2 n,$

( 9.1)

и чтобы сравнить, насколько быстрее могут быть упорядочены данные при использовании параллельных вычислений, в обязательном порядке должна применяться именно эта оценка сложности. Как основной результат приведенных рассуждений, можно сформулировать утверждение о том, что при определении показателей ускорения и эффективности параллельных вычислений в качестве оценки сложности последовательного способа решения рассматриваемой задачи следует использовать трудоемкость наилучших последовательных алгоритмов. Параллельные методы решения задач должны сравниваться с наиболее быстродействующими последовательными способами вычислений!

Определим теперь сложность рассмотренного параллельного алгоритма упорядочивания данных. Как отмечалось ранее, на начальной стадии работы метода каждый процессор проводит упорядочивание своих блоков данных (размер блоков при равномерном распределении данных равен n/p ). Предположим, что данная начальная сортировка может быть выполнена при помощи быстродействующих алгоритмов упорядочивания данных, тогда трудоемкость начальной стадии вычислений можно определить выражением вида:

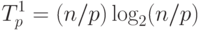$T_p^1=(n/p) \log_2 (n/p)$

( 9.2)

Далее, на каждой выполняемой итерации параллельной сортировки взаимодействующие пары процессоров осуществляют передачу блоков между собой, после чего получаемые на каждом процессоре пары блоков объединяются при помощи процедуры слияния. Общее количество итераций не превышает величины p, и, как результат, общее количество операций этой части параллельных вычислений оказывается равным

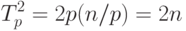( 9.3)

С учетом полученных соотношений показатели эффективности и ускорения параллельного метода сортировки имеют вид:

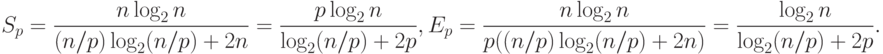$S_p= \frac{n \log_2 n}{(n/p)\log_2(n/p)+2n} = \frac{p \log_2 n}{\log_2(n/p)+2p},\\ E_p= \frac{n \log_2 n}{p((n/p)\log_2(n/p)+2n)} = \frac{\log_2 n}{\log_2(n/p)+2p} .$

( 9.4)

Расширим приведенные выражения – учтем длительность выполняемых вычислительных операций и оценим трудоемкость операции передачи блоков между процессорами. При использовании модели Хокни общее время всех выполняемых в ходе сортировки операций передачи блоков можно оценить при помощи соотношения вида:

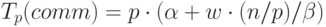$T_p(comm)=p \cdot (\alpha + w \cdot (n/p)/ \beta)$

( 9.5)

где $\alpha$ – латентность, $\beta$ – пропускная способность сети передачи данных, а w есть размер элемента упорядочиваемых данных в байтах.

С учетом трудоемкости коммуникационных действий общее время выполнения параллельного алгоритма сортировки определяется следующим выражением:

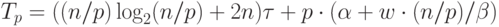$T_p=((n/p)\log_2(n/p)+2n)\tau+p\cdot(\alpha + w \cdot (n/p)/ \beta)$

( 9.6)

где $\tau$ есть время выполнения базовой операции сортировки.

9.3.6. Результаты вычислительных экспериментов

Эксперименты осуществлялись на вычислительном кластере Нижегородского университета на базе процессоров Intel Xeon 4 EM64T, 3000 МГц и сети Gigabit Ethernet под управлением операционной системы Microsoft Windows Server 2003 Standard x64 Edition и системы управления кластером Microsoft Compute Cluster Server.

Для оценки длительности $\tau$ базовой скалярной операции алгоритма сортировки проводилось решение задачи упорядочивания при помощи последовательного алгоритма и полученное таким образом время вычислений делилось на общее количество выполненных операций – в результате выполненных экспериментов для величины $\tau$ было получено значение 10,41 нсек. Эксперименты, выполненные для определения параметров сети передачи данных, показали значения латентности $\alpha$ и пропускной способности $\beta$ соответственно 130 мкс и 53,29 Мбайт/с. Все вычисления производились над числовыми значениями типа double, размер которого на данной платформе равен 8 байт (следовательно w=8 ).

Результаты вычислительных экспериментов приведены в табл. 9.2. Эксперименты выполнялись с использованием двух и четырех процессоров.

Таблица 9.2. Результаты вычислительных экспериментов для параллельного алгоритма пузырьковой сортировки
Количество элементов	Последовательный алгоритм	Параллельный алгоритм
		2 процессора		4 процессора
		Время	Ускорение	Время	Ускорение
10000	0,001422	0,002210	0,643439	0,003270	0,434862
20000	0,002991	0,004428	0,675474	0,004596	0,650783
30000	0,004612	0,006745	0,683766	0,006873	0,671032
40000	0,006297	0,008033	0,783891	0,009107	0,691446
50000	0,008014	0,009770	0,820266	0,010840	0,739299

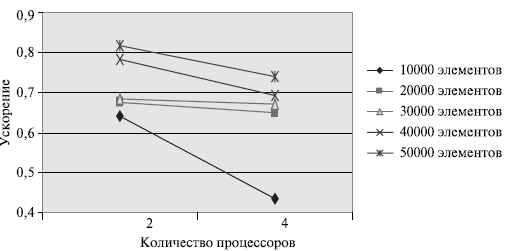
Рис. 9.1. Зависимость ускорения от количества процессоров при выполнении параллельного алгоритма пузырьковой сортировки

Как можно заметить из приведенных результатов вычислительных экспериментов, параллельный вариант алгоритма сортировки работает медленнее исходного последовательного метода пузырьковой сортировки, т.к. объем передаваемых данных между процессорами является достаточно большим и сопоставим с количеством выполняемых вычислительных операций (и этот дисбаланс объема вычислений и сложности операций передачи данных увеличивается с ростом числа процессоров).

Сравнение времени выполнения эксперимента 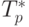T^*_p и теоретической оценки T_p из (9.6) приведено в таблице 9.3 и на рис. 9.2.

Таблица 9.3. Сравнение экспериментального и теоретического времени выполнения параллельного алгоритма пузырьковой сортировки
Количество элементов	Параллельный алгоритм
	2 процессора		4 процессора

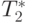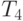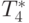10000	0,002003	0,002210	0,002057	0,003270
20000	0,003709	0,004428	0,003366	0,004596
30000	0,005455	0,006745	0,004694	0,006873
40000	0,007227	0,008033	0,006035	0,009107
50000	0,009018	0,009770	0,007386	0,010840