НОУ ИНТУИТ | Теория и практика параллельных вычислений. Лекция 3: Оценка коммуникационной трудоемкости параллельных алгоритмов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.07.2007 | Доступ: свободный | Студентов: 2035 / 507 | Оценка: 4.53 / 4.26 | Длительность: 25:10:00

ISBN: 978-5-9556-0096-3

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.3. Методы логического представления топологии коммуникационной среды

Как показало рассмотрение основных коммуникационных операций в подразделе 3.1, ряд алгоритмов передачи данных допускает более простое изложение при использовании вполне определенных топологий сети межпроцессорных соединений. Кроме того, многие методы коммуникации могут быть получены при помощи того или иного логического представления исследуемой топологии. Как результат, важным моментом при организации параллельных вычислений является возможность логического представления разнообразных топологий на основе конкретных (физических) межпроцессорных структур.

Способы логического представления (отображения) топологий характеризуются следующими тремя основными характеристиками:

уплотнение дуг ( congestion ), выражаемое как максимальное количество дуг логической топологии, которые отображаются в одну линию передачи физической топологии;
удлинение дуг ( dilation ), определяемое как путь максимальной длины физической топологии, на который отображается дуга логической топологии;
увеличение вершин ( expansion ), вычисляемое как отношение количества вершин в логической и физической топологиях.

Для рассматриваемых в рамках пособия топологий ограничимся изложением вопросов отображения топологий кольца и решетки на гиперкуб. Предлагаемые ниже подходы для логического представления топологий характеризуются единичными показателями уплотнения и удлинения дуг.

3.3.1. Представление кольцевой топологии в виде гиперкуба

Установление соответствия между кольцевой топологией и гиперкубом может быть выполнено при помощи двоичного рефлексивного кода Грея G(i, N) ( binary reflected Gray code ), определяемого в соответствии с выражениями:

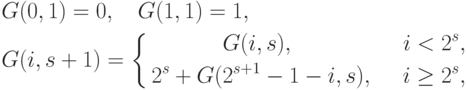$\begin{aligned} &G(0,1)=0, \quad G(1,1)=1, \\ &G(i,s+1)= \left\{ \begin{aligned} &G(i,s), & i < 2^s, \\ 2^s + G(&2^{s+1} - 1 -i,s), \quad & i \ge 2^s, \end{aligned} \right. \end{aligned}$

( 3.22)

где i задает номер значения в коде Грея, а N есть длина этого кода. Для иллюстрации подхода в табл. 3.1 показывается отображение кольцевой топологии на гиперкуб для сети из p=8 процессоров.

Важное свойство кода Грея: соседние значения G(i,N) и G(i+1,N) имеют только одну различающуюся битовую позицию. Как результат, соседние вершины в кольцевой топологии отображаются на соседние процессоры в гиперкубе.

Таблица 3.1. Отображение кольцевой топологии на гиперкуб при помощи кода Грея
Код Грея для N=1	Код Грея для N=2	Код Грея для N=3	Номера процессоров
Код Грея для N=1	Код Грея для N=2	Код Грея для N=3	гиперкуба	кольца
0	0 0	0 0 0	0	0
1	0 1	0 0 1	1	1
	1 1	0 1 1	3	2
	1 0	0 1 0	2	3
		1 1 0	6	4
		1 1 1	7	5
		1 0 1	5	6
		1 0 0	4	7

3.3.2. Отображение топологии решетки на гиперкуб

Отображение топологии решетки на гиперкуб может быть выполнено в рамках подхода, использованного для кольцевой структуры сети.

Тогда для отображения решетки $2^r \times 2^s$ на гиперкуб размерности N=r+s можно принять правило, что элементу решетки с координатами (i, j) соответствует процессор гиперкуба с номером:

G(i,r)||G(j,s),

где операция || означает конкатенацию кодов Грея.

3.4. Оценка трудоемкости операций передачи данных для кластерных систем

Для кластерных вычислительных систем (см. п. 1.2.2) одним из широко применяемых способов построения коммуникационной среды является использование концентраторов ( hub ) или коммуникаторов ( switch ) для объединения процессорных узлов кластера в единую вычислительную сеть. В этих случаях топология сети кластера представляет собой полный граф, в котором, однако, имеются определенные ограничения на одновременность выполнения коммуникационных операций. Так, при использовании концентраторов передача данных в каждый текущий момент может выполняться только между двумя процессорными узлами; коммуникаторы могут обеспечивать взаимодействие нескольких непересекающихся пар процессоров.

Другое часто применяемое решение при создании кластеров состоит в использовании метода передачи пакетов (часто реализуемого на основе стека протоколов TCP/IP) в качестве основного способа выполнения коммуникационных операций.

Если выбрать для дальнейшего анализа кластеры данного распространенного типа (топология в виде полного графа, пакетный способ передачи сообщений), то трудоемкость операции коммуникации между двумя процессорными узлами может быть оценена в соответствии с выражением ( модель А )

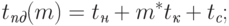$t_{\textit{пд}}(m) = t_{\textit{н}} + m^*t_{\textit{к}} + t_{\textit{с}};$

( 3.23)

оценка подобного вида следует из соотношений для метода передачи пакетов при единичной длине пути передачи данных, т.е. при l=1. Отмечая возможность подобного подхода, вместе с этим можно заметить, что в рамках рассматриваемой модели время подготовки данных t_н предполагается постоянным (не зависящим от объема передаваемых данных), время передачи служебных данных t_с не зависит от количества передаваемых пакетов и т.п. Эти предположения не в полной мере соответствуют действительности, и временные оценки, получаемые в результате использования модели, могут не обладать необходимой точностью.

С учетом приведенных замечаний, схема построения временных оценок может быть уточнена; в рамках новой расширенной модели трудоемкость передачи данных между двумя процессорами определяется в соответствии со следующими выражениями ( модель В ):

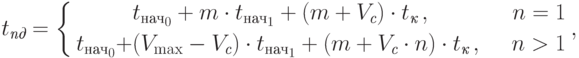$t_{\textit{пд}} = \left\{ \begin{aligned} & t_{\text{нач}_0} + m \cdot t_{\text{нач}_1} + (m + V_{\textit{с}}) \cdot t_{\textit{к}} \, , & n=1 \\ t_{\text{нач}_0} + & (V_{\max}- V_{\textit{с}}) \cdot t_{\text{нач}_1} + (m + V_{\textit{с}} \cdot n) \cdot t_{\textit{к}} \, , \quad & n > 1 \end{aligned} \right. ,$

( 3.24)

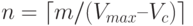где $n=\lceil m/(V_{max}–V_c)\rceil$ есть количество пакетов, на которое разбивается передаваемое сообщение, величина V_max определяет максимальный размер пакета, который может быть доставлен в сети (по умолчанию для операционной системы MS Windows в сети Fast Ethernet V_max=1500 байт), а V_c есть объем служебных данных в каждом из пересылаемых пакетов (для протокола TCP/IP, ОС Windows 2000 и сети Fast Ethernet V_c=78 байт). Поясним также, что в приведенных соотношениях константа $t_{\textit{нач}_0}$ характеризует аппаратную составляющую латентности и зависит от параметров используемого сетевого оборудования, значение $t_{\textit{нач}_1}$ задает время подготовки одного байта данных для передачи по сети. Как результат, величина латентности

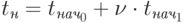$t_{\textit{н}} = t_{\textit{нач}_0} + \nu \cdot t_{\textit{нач}_1}$

( 3.25)

увеличивается линейно в зависимости от объема передаваемых данных. При этом предполагается, что подготовка данных для передачи второго и всех последующих пакетов может быть совмещена с пересылкой по сети предшествующих пакетов и латентность, тем самым, не может превышать величины:

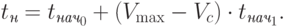$t_{\textit{н}} = t_{\textit{нач}_0} + (V_{\max}-V_c) \cdot t_{\textit{нач}_1}.$

( 3.26)

Помимо латентности, в предлагаемых выражениях для оценки трудоемкости коммуникационной операции можно уточнить также правило вычисления времени передачи данных

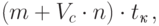$(m + V_c \cdot n) \cdot t_{\textit{к}} \, ,$

( 3.27)

что позволяет теперь учитывать эффект увеличения объема передаваемых данных при росте числа пересылаемых пакетов за счет добавления служебной информации (заголовков пакетов).

Завершая анализ проблемы построения теоретических оценок трудоемкости коммуникационных операций, следует отметить, что для практического применения перечисленных моделей необходимо выполнить оценку значений параметров используемых соотношений. В этом отношении полезным может оказаться использование и более простых способов вычисления временных затрат на передачу данных – одной из известных схем подобного вида является подход, в котором трудоемкость операции коммуникации между двумя процессорными узлами кластера оценивается в соответствии с выражением:

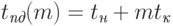$t_{\textit{пд}}(m) = t_{\textit{н}} + mt_{\textit{к}}$

( 3.28)

это модель C, предложенная Хокни ( the Hockney model ) – см., например, [46].

Для проверки адекватности рассмотренных моделей реальным процессам передачи данных приведем результаты выполненных экспериментов в сети многопроцессорного кластера Нижегородского университета (компьютеры IBM PC Pentium 4 1300 MГц и сеть Fast Etherrnet). При проведении экспериментов для реализации коммуникационных операций использовалась библиотека MPI.

Часть экспериментов была выполнена для оценки параметров моделей:

значение латентности t_н для моделей A и C определялось как время передачи сообщения нулевой длины;
величина пропускной способности R оценивалась максимальным значением скорости передачи данных, наблюдавшимся в экспериментах, т.е. величиной
$R=\max_m(t_{\textit{пд}}(m)/m) ,$
и полагалось t_к=1/R ;
значения величин $t_{\textit{нач}_0}$ и $t_{\textit{нач}_1}$ оценивались при помощи линейной аппроксимации времен передачи сообщений размера от 0 до V_max.

В ходе экспериментов осуществлялась передача данных между двумя узлами кластера, размер передаваемых сообщений варьировался от 0 до 8 Мб. Для получения более точных оценок выполнение каждой операции осуществлялось многократно (более 100 000 раз), после чего полученные результаты усреднялись. Для иллюстрации ниже приведен результат одного эксперимента, при проведении которого размер передаваемых сообщений изменялся от 2000 до 60 000 байт.

В табл. 3.2 приводится ряд числовых данных по погрешности рассмотренных моделей трудоемкости коммуникационных операций (величина погрешности дается в виде относительного отклонения от реального времени выполнения операции передачи данных).

Таблица 3.2. Погрешность моделей трудоемкости операций передачи данных (по результатам вычислительных экспериментов)
Объем сообщения (байт)	Время передачи (мкс)	Погрешимость теоретической оценки времени передачи данных, %
Объем сообщения (байт)	Время передачи (мкс)	Модель A	Модель B	Модель C
2000	495	33,45	7,93	34,80
10000	1184	13,91	1,70	14,48
20000	2055	8,44	0,44	8,77
30000	2874	4,53	-1,87	4,76
40000	3758	4,04	-1,38	4,22
50000	4749	5,91	1,21	6,05
60000	5730	6,97	2,73	7,09

Как можно заметить по результатам проведенных экспериментов, оценки трудоемкости операций передачи данных по модели B имеют меньшую погрешность.

Вместе с этим важно отметить, что для предварительного анализа временных затрат на выполнение коммуникационных операций точности модели C может оказаться достаточно. Кроме того, данная модель имеет наиболее простой вид среди всех рассмотренных. С учетом последнего обстоятельства, далее во всех последующих лекциях для оценки трудоемкости операций передачи данных будет применяться именно модель C (модель Хокни), при этом для модели будет использоваться форма записи, приведенная к обозначениям, которые приняты в работе Хокни [46]:

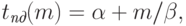$t_{\textit{пд}}(m) = \alpha + m/ \beta,$

( 3.29)

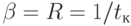где $\alpha$ есть латентность сети передачи данных (т.е. $\alpha =t_{н}$ ), а $\beta$ обозначает пропускную способность сети (т.е. $\beta =R=1/t_{к}$ ).

Дальше >>

Авторизоваться

Теория и практика параллельных вычислений

Оценка коммуникационной трудоемкости параллельных алгоритмов

3.3. Методы логического представления топологии коммуникационной среды

3.3.1. Представление кольцевой топологии в виде гиперкуба

3.3.2. Отображение топологии решетки на гиперкуб

3.4. Оценка трудоемкости операций передачи данных для кластерных систем

Вопросы и ответы