Оценка коммуникационной трудоемкости параллельных алгоритмов
3.2.3. Передача данных от всех процессоров всем процессорам сети
Операция передачи данных от всех процессоров всем процессорам сети ( all-to-all broadcast или multinode broadcast ) является естественным обобщением одиночной операции рассылки, двойственная ей операция – прием сообщений на каждом процессоре от всех процессоров сети ( multinode accumulation ). Подобные операции широко используются, например, при реализации матричных вычислений.
Возможный способ реализации операции множественной рассылки состоит в выполнении соответствующего набора операций одиночной рассылки. Однако такой подход не является оптимальным для многих топологий сети, поскольку часть необходимых операций одиночной рассылки потенциально может быть выполнена параллельно. Как и ранее, материал будет рассматриваться раздельно для разных методов передачи данных (см. п. 3.1.2).
Передача сообщений. Для кольцевой топологии каждый процессор может инициировать рассылку своего сообщения одновременно (в каком-либо выбранном направлении по кольцу). В любой момент каждый процессор выполняет прием и передачу данных, завершение операции множественной рассылки произойдет через p-1 цикл передачи данных. Длительность выполнения операции рассылки оценивается соотношением:
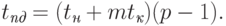 |
( 3.9) |
Для топологии типа решетка-тор множественная рассылка
сообщений может быть выполнена при помощи алгоритма, получаемого
обобщением способа передачи данных для кольцевой структуры сети.
Схема обобщения состоит в следующем. На первом этапе организуется
передача сообщений раздельно по всем процессорам сети,
располагающимся на одних и тех же горизонталях решетки (в
результате на каждом процессоре одной и той же горизонтали
формируются укрупненные сообщения размера 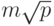 ,
объединяющие все сообщения горизонтали). Время выполнения этапа:
,
объединяющие все сообщения горизонтали). Время выполнения этапа:
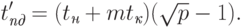
На втором этапе рассылка данных выполняется по процессорам сети, образующим вертикали решетки. Длительность этого этапа:
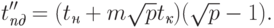
Общая длительность операции рассылки определяется соотношением:
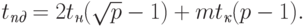 |
( 3.10) |
Для гиперкуба алгоритм множественной рассылки сообщений может быть получен путем обобщения ранее описанного способа передачи данных для топологии типа решетки на размерность гиперкуба N. В результате такого обобщения схема коммуникации состоит в следующем. На каждом этапе i, 1<=i<=N, выполнения алгоритма функционируют все процессоры сети, которые обмениваются своими данными со своими соседями по i -ой размерности и формируют объединенные сообщения. Время операции рассылки может быть получено при помощи выражения:
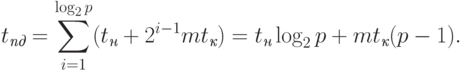 |
( 3.11) |
Передача пакетов. Применение более эффективного для кольцевой структуры и топологии типа решетка-тор метода передачи данных не приводит к какому-либо улучшению времени выполнения операции множественной рассылки, поскольку обобщение алгоритмов выполнения операции одиночной рассылки на случай множественной рассылки приводит к перегрузке каналов передачи данных (т.е. к существованию ситуаций, когда в один и тот же момент для передачи по одной и той же линии имеется несколько ожидающих пересылки пакетов данных). Перегрузка каналов приводит к задержкам при пересылках данных, что и не позволяет проявиться всем преимуществам метода передачи пакетов.
Широко распространенным примером операции множественной рассылки является задача редукции ( reduction ), которая определяется в общем виде как процедура выполнения той или иной обработки данных, получаемых на каждом процессоре в ходе множественной рассылки (в качестве примера такой задачи может быть рассмотрена проблема вычисления суммы значений, находящихся на разных процессорах, и рассылки полученной суммы по всем процессорам сети). Способы решения задачи редукции могут состоять в следующем:
- непосредственный подход заключается в выполнении операции множественной рассылки и последующей затем обработке данных на каждом процессоре в отдельности;
- более эффективный алгоритм может быть получен в результате применения операции одиночного приема данных на отдельном процессоре, выполнения на этом процессоре действий по обработке данных и рассылки полученного результата обработки всем процессорам сети;
- наилучший же способ решения задачи редукции состоит в
совмещении процедуры множественной рассылки и действий по
обработке данных, когда каждый процессор сразу же после приема
очередного сообщения реализует требуемую обработку полученных
данных (например, выполняет сложение полученного значения с
имеющейся на процессоре частичной суммой). Время решения задачи
редукции при таком алгоритме реализации в случае, например,
когда размер пересылаемых данных имеет единичную длину (m=1) и топология сети имеет структуру гиперкуба,
определяется выражением:
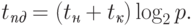
( 3.12)
Другим типовым примером использования операции множественной рассылки является задача нахождения частных сумм последовательности значений Si (в англоязычной литературе эта задача известна под названием prefix sum problem )
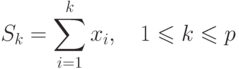 |
( 3.13) |
Алгоритм решения данной задачи также может быть получен при помощи конкретизации общего способа выполнения множественной операции рассылки, когда процессор выполняет суммирование полученного значения (но только в том случае, если процессор – отправитель значения имеет меньший номер, чем процессор-получатель).
3.2.4. Обобщенная передача данных от одного процессора всем остальным процессорам сети
Общий случай передачи данных от одного процессора всем остальным процессорам сети состоит в том, что все рассылаемые сообщения являются различными ( one-to-all personalized communication или single-node scatter ). Двойственная операция передачи для данного типа взаимодействия процессоров – обобщенный прием сообщений ( single-node gather ) на одном процессоре от всех остальных процессоров сети (отличие данной операции от ранее рассмотренной процедуры сборки данных на одном процессоре состоит в том, что обобщенная операция сборки не предполагает какого-либо взаимодействия сообщений (например, редукции) в процессе передачи данных).
Трудоемкость операции обобщенной рассылки сопоставима со сложностью выполнения процедуры множественной передачи данных. Процессор – инициатор рассылки посылает каждому процессору сети сообщение размера m, и, тем самым, нижняя оценка длительности выполнения операции характеризуется величиной mtk(p–1).
Проведем более подробный анализ трудоемкости обобщенной рассылки для случая топологии типа гиперкуб. Возможный способ выполнения операции состоит в следующем. Процессор – инициатор рассылки передает половину своих сообщений одному из своих соседей (например, по первой размерности) – в результате исходный гиперкуб становится разделенным на два гиперкуба половинного размера, в каждом из которых содержится ровно половина исходных данных. Далее, действия по рассылке сообщений могут быть повторены, и общее количество повторений определяется исходной размерностью гиперкуба. Длительность операции обобщенной рассылки может быть охарактеризована соотношением:
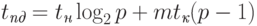 |
( 3.14) |
