НОУ ИНТУИТ | Теория и практика параллельных вычислений. Лекция 3: Оценка коммуникационной трудоемкости параллельных алгоритмов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.07.2007 | Доступ: свободный | Студентов: 2035 / 507 | Оценка: 4.53 / 4.26 | Длительность: 25:10:00

ISBN: 978-5-9556-0096-3

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.2. Анализ трудоемкости основных операций передачи данных

При всем разнообразии выполняемых операций передачи данных при параллельных способах решения сложных научно-технических задач, определенные процедуры взаимодействия процессоров сети могут быть отнесены к числу основных коммуникационных действий, либо наиболее широко распространенных в практике параллельных вычислений, либо тех, к которым могут быть сведены многие другие процессы приема-передачи сообщений. Важно отметить также, что в рамках подобного базового набора для большинства операций коммуникации существуют процедуры, обратные по действию исходным операциям (так, например, операции передачи данных от одного процессора всем имеющимся процессорам сети соответствует операция приема в одном процессоре сообщений от всех остальных процессоров). Как результат, рассмотрение коммуникационных процедур целесообразно выполнять попарно, поскольку во многих случаях алгоритмы выполнения прямой и обратной операций могут быть получены исходя из одинаковых предпосылок.

Рассмотрение основных операций передачи данных в этой лекции будет осуществляться на примере таких топологий сети, как кольцо, двумерная решетка и гиперкуб. Для двумерной решетки будет предполагаться также, что между граничными процессорами в строках и столбцах решетки имеются каналы передачи данных (т.е. топология сети представляет собой тор). Как и ранее, величина m будет означать размер сообщения в словах, значение p определяет количество процессоров в сети, а переменная N задает размерность топологии гиперкуба.

3.2.1. Передача данных между двумя процессорами сети

Трудоемкость данной коммуникационной операции может быть получена путем подстановки длины максимального пути (диаметра сети) в выражения для времени передачи данных при разных методах коммуникации (см. п. 3.1.2) – см. табл. 3.1.

Таблица 3.1. Время передачи данных между двумя процессорами
Топология	Передача сообщений	Передача пакетов
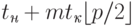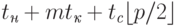Кольцо	$t_{\textit{н}} + mt_{\textit{к}} \lfloor p/2 \rfloor$	$t_{\textit{н}} + mt_{\textit{к}} + t_{\textit{с}} \lfloor p/2 \rfloor$
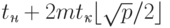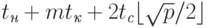Решетка-тор	$t_{\textit{н}} + 2mt_{\textit{к}} \lfloor \sqrt{p}/2 \rfloor$	$t_{\textit{н}} + mt_{\textit{к}} +2t_{\textit{с}} \lfloor \sqrt{p}/2 \rfloor$
Гиперкуб	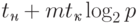$t_{\textit{н}} + mt_{\textit{к}} \log_2 p$	$t_{\textit{н}} + mt_{\textit{к}} + t_{\textit{с}} \log_2 p$

3.2.2. Передача данных от одного процессора всем остальным процессорам сети

Операция передачи данных (одного и того же сообщения) от одного процессора всем остальным процессорам сети ( one-to-all broadcast или single-node broadcast ) является одним из наиболее часто выполняемых коммуникационных действий. Двойственная ей операция – прием на одном процессоре сообщений от всех остальных процессоров сети ( single-node accumulation ). Подобные операции используются, в частности, при реализации матрично-векторного умножения, решении систем линейных уравнений методом Гаусса, решении задачи поиска кратчайших путей и др.

Простейший способ реализации операции рассылки состоит в ее выполнении как последовательности попарных взаимодействий процессоров сети. Однако при таком подходе большая часть пересылок является избыточной и возможно применение более эффективных алгоритмов коммуникации. Изложение материала будет проводиться сначала для метода передачи сообщений, затем – для пакетного способа передачи данных (см. п. 3.1.2).

Передача сообщений. Для кольцевой топологии процессор – источник рассылки может инициировать передачу данных сразу двум своим соседям, которые, в свою очередь, приняв сообщение, организуют пересылку далее по кольцу. Трудоемкость выполнения операции рассылки в этом случае будет определяться соотношением:

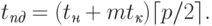$t_{\textit{пд}} = (t_{\textit{н}} + mt_{\textit{к}}) \lceil p/2 \rceil.$

( 3.4)

Для топологии типа решетка-тор алгоритм рассылки может быть получен из способа передачи данных, примененного для кольцевой структуры сети. Так, рассылка может быть выполнена в виде двухэтапной процедуры. На первом этапе организуется передача сообщения всем процессорам сети, располагающимся на той же горизонтали решетки, что и процессор – инициатор передачи. На втором этапе процессоры, получившие копию данных на первом этапе, рассылают сообщения по своим соответствующим вертикалям. Оценка длительности операции рассылки в соответствии с описанным алгоритмом определяется соотношением:

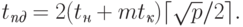$t_{\textit{пд}} = 2(t_{\textit{н}} + mt_{\textit{к}}) \lceil \sqrt{p}/2 \rceil.$

( 3.5)

Для гиперкуба рассылка может быть выполнена в ходе N-этапной процедуры передачи данных. На первом этапе процессор-источник сообщения передает данные одному из своих соседей (например, по первой размерности) – в результате после первого этапа есть два процессора, имеющих копию пересылаемых данных (данный результат можно интерпретировать также как разбиение исходного гиперкуба на два таких одинаковых по размеру гиперкуба размерности N-1, что каждый из них имеет копию исходного сообщения). На втором этапе два процессора, задействованные на первом этапе, пересылают сообщение своим соседям по второй размерности и т.д. В результате такой рассылки время операции оценивается при помощи выражения:

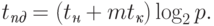$t_{\textit{пд}} = (t_{\textit{н}} + mt_{\textit{к}}) \log_2 p .$

( 3.6)

Сравнивая полученные выражения для длительности выполнения операции рассылки, можно отметить, что наилучшие показатели имеет топология типа гиперкуб; более того, можно показать, что данный результат является наилучшим для выбранного способа коммуникации с помощью передачи сообщений.

Передача пакетов. Для топологии типа кольцо алгоритм рассылки может быть получен путем логического представления кольцевой структуры сети в виде гиперкуба. В результате на этапе рассылки процессор – источник сообщения передает данные процессору, находящемуся на расстоянии p/2 от исходного процессора. Далее, на втором этапе оба процессора, уже имеющие рассылаемые данные после первого этапа, передают сообщения процессорам, находящимся на расстоянии p/4, и т.д. Трудоемкость выполнения операции рассылки при таком методе передачи данных определяется соотношением:

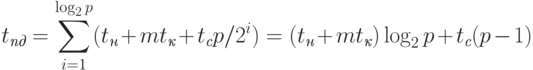$t_{\textit{пд}} = \sum_{i=1}^{\log_2 p}(t_{\textit{н}} + mt_{\textit{к}} + t_{\textit{с}} p/2^i) = (t_{\textit{н}} + mt_{\textit{к}}) \log_2 p + t_{\textit{с}}(p-1)$

( 3.7)

(как и ранее, при достаточно больших сообщениях временем передачи служебных данных можно пренебречь).

Для топологии типа решетка-тор алгоритм рассылки может быть получен из способа передачи данных, примененного для кольцевой структуры сети, в соответствии с тем же способом обобщения, что и в случае использования метода передачи сообщений. Получаемый в результате такого обобщения алгоритм рассылки характеризуется следующим соотношением для оценки времени выполнения:

$t_{\textit{пд}} = (t_{\textit{н}} + mt_{\textit{к}}) \log_2 p + 2 t_{\textit{с}} (\sqrt{p} - 1).$

( 3.8)

Для гиперкуба алгоритм рассылки (и, соответственно, временные оценки длительности выполнения) при передаче пакетов не отличается от варианта для метода передачи сообщений.

Дальше >>

Авторизоваться

Теория и практика параллельных вычислений

Оценка коммуникационной трудоемкости параллельных алгоритмов

3.2. Анализ трудоемкости основных операций передачи данных

3.2.1. Передача данных между двумя процессорами сети

3.2.2. Передача данных от одного процессора всем остальным процессорам сети

Вопросы и ответы