Оценка коммуникационной трудоемкости параллельных алгоритмов
3.2.5. Обобщенная передача данных от всех процессоров всем процессорам сети
Обобщенная передача данных от всех процессоров всем процессорам сети ( total exchange ) представляет собой наиболее общий случай коммуникационных действий. Необходимость выполнения подобных операций возникает в параллельных алгоритмах быстрого преобразования Фурье, транспонирования матриц и др.
Выполним краткую характеристику возможных способов выполнения обобщенной множественной рассылки для разных методов передачи данных (см. п. 3.1.2).
Передача сообщений. Общая схема алгоритма для кольцевой топологии состоит в следующем. Каждый процессор производит передачу всех своих исходных сообщений своему соседу (в каком-либо выбранном направлении по кольцу). Далее процессоры осуществляют прием направленных к ним данных, затем среди принятой информации выбирают свои сообщения, после чего выполняют дальнейшую рассылку оставшейся части данных. Длительность выполнения подобного набора передач данных оценивается при помощи выражения:
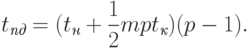 |
( 3.15) |
Способ получения алгоритма рассылки данных для топологии типа решетка-тор является тем же самым, что и в случае рассмотрения других коммуникационных операций. На первом этапе организуется передача сообщений раздельно по всем процессорам сети, располагающимся на одних и тех же горизонталях решетки (каждому процессору по горизонтали передаются только те исходные сообщения, что должны быть направлены процессорам соответствующей вертикали решетки). После завершения этапа на каждом процессоре собираются p сообщений, предназначенных для рассылки по одной из вертикалей решетки. На втором этапе рассылка данных выполняется по процессорам сети, образующим вертикали решетки. Общая длительность всех операций рассылок определяется соотношением:
 |
( 3.16) |
Для гиперкуба алгоритм обобщенной множественной рассылки сообщений может быть получен путем обобщения способа выполнения операции для топологии типа решетка на размерность гиперкуба N. В результате такого обобщения схема коммуникации состоит в следующем. На каждом этапе i, 1<=i<=N, выполнения алгоритма функционируют все процессоры сети, которые обмениваются своими данными со своими соседями по i -й размерности и формируют объединенные сообщения. При организации взаимодействия двух соседей канал связи между ними рассматривается как связующий элемент двух равных по размеру подгиперкубов исходного гиперкуба, и каждый процессор пары посылает другому процессору только те сообщения, что предназначены для процессоров соседнего подгиперкуба. Время операции рассылки может быть получено при помощи выражения:
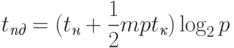 |
( 3.17) |
 операций по сортировке своих сообщений
перед обменом информацией со своими соседями).
операций по сортировке своих сообщений
перед обменом информацией со своими соседями).Передача пакетов. Как и в случае множественной рассылки, применение метода передачи пакетов не приводит к улучшению временных характеристик для операции обобщенной множественной рассылки. Рассмотрим как пример более подробно выполнение данной коммуникационной операции для сети с топологией типа гиперкуб. В этом случае рассылка может быть выполнена за p-1 итерацию. На каждой итерации все процессоры разбиваются на взаимодействующие пары процессоров, причем это разбиение на пары может быть выполнено таким образом, чтобы передаваемые между разными парами сообщения не использовали одни и те же пути передачи данных. Как результат, общая длительность операции обобщенной рассылки может быть определена в соответствии с выражением:
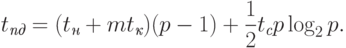 |
( 3.18) |
3.2.6. Циклический сдвиг
Частный случай обобщенной множественной рассылки есть процедура перестановки
( permutation ), представляющая собой
операцию перераспределения информации между процессорами сети, в
которой каждый процессор передает сообщение определенному неким
способом другому процессору сети. Конкретный вариант перестановки
– циклический q-сдвиг
( cirlular q-shift ), при котором каждый
процессор i, 1<=i<=N, передает данные процессору
с номером 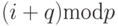 . Подобная операция сдвига
используется, например, при организации матричных вычислений.
. Подобная операция сдвига
используется, например, при организации матричных вычислений.
Поскольку выполнение циклического сдвига для кольцевой топологии может быть обеспечено при помощи простых алгоритмов передачи данных, рассмотрим возможные способы выполнения данной коммуникационной операции только для топологий решетка-тор и гиперкуб при разных методах передачи данных (см. п. 3.1.2).
Передача сообщений. Общая схема алгоритма циклического
сдвига для топологии типа решетка-тор состоит в следующем.
Пусть процессоры перенумерованы по строкам решетки от 0 до p-1. На первом этапе организуется
циклический сдвиг с шагом  по
каждой строке в отдельности (если при реализации такого сдвига
сообщения передаются через правые границы строк, то после
выполнения каждой такой передачи необходимо осуществить
компенсационный сдвиг вверх на 1 для процессоров первого столбца
решетки). На втором этапе реализуется циклический сдвиг вверх
с шагом
по
каждой строке в отдельности (если при реализации такого сдвига
сообщения передаются через правые границы строк, то после
выполнения каждой такой передачи необходимо осуществить
компенсационный сдвиг вверх на 1 для процессоров первого столбца
решетки). На втором этапе реализуется циклический сдвиг вверх
с шагом 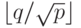 для каждого
столбца решетки. Общая длительность всех операций рассылок
определяется соотношением:
для каждого
столбца решетки. Общая длительность всех операций рассылок
определяется соотношением:
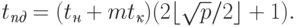 |
( 3.19) |
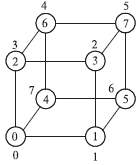
Для гиперкуба алгоритм циклического сдвига может быть получен путем логического представления топологии гиперкуба в виде кольцевой структуры. Для получения такого представления установим взаимно-однозначное соответствие между вершинами кольца и гиперкуба. Необходимое соответствие может быть получено, например, при помощи известного кода Грея. Более подробное изложение механизма установки такого соответствия осуществляется в подразделе 3.3; для наглядности на рис. 3.1 приводится вид гиперкуба для размерности N=3 с указанием для каждого процессора гиперкуба соответствующей вершины кольца. Положительным свойством выбора такого соответствия является тот факт, что для любых двух вершин в кольце, расстояние между которыми равно l=2i для некоторого значения i, путь между соответствующими вершинами в гиперкубе содержит только две линии связи (за исключением случая i=0, когда путь в гиперкубе имеет единичную длину).
Представим величину сдвига q в виде двоичного кода. Количество ненулевых позиций кода определяет количество этапов в схеме реализации операции циклического сдвига. На каждом этапе выполняется операция сдвига с величиной шага, задаваемой наиболее старшей ненулевой позицией значения q (например, при исходной величине сдвига q=5=1012 на первом этапе выполняется сдвиг с шагом 4, на втором этапе шаг сдвига равен 1). Выполнение каждого этапа (кроме сдвига с шагом 1) состоит в передаче данных по пути, включающему две линии связи. Как результат, верхняя оценка для длительности выполнения операции циклического сдвига определяется соотношением:
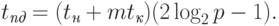 |
( 3.20) |
Передача пакетов. Использование пересылки пакетов
может повысить эффективность выполнения операции циклического
сдвига для топологии гиперкуб. Реализация всех необходимых
коммуникационных действий в этом случае может быть обеспечена
путем отправления каждым процессором всех пересылаемых данных
непосредственно процессорам назначения. Применение метода
покоординатной маршрутизации (см. п. 3.1.1) позволит избежать
коллизий при использовании линий передачи данных (в каждый
момент времени для каждого канала будет существовать не более
одного готового для отправки сообщения). Длина наибольшего
пути при такой рассылке данных определяется как  , где
, где 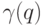 есть наибольшее целое значение j такое, что 2j есть
делитель величины сдвига q. Тогда длительность операции циклического сдвига может быть охарактеризована при
помощи выражения
есть наибольшее целое значение j такое, что 2j есть
делитель величины сдвига q. Тогда длительность операции циклического сдвига может быть охарактеризована при
помощи выражения
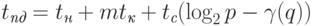 |
( 3.21) |
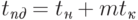 ).
).