Моделирование и анализ параллельных вычислений

2.4. Показатели эффективности параллельного алгоритма

Ускорение ( speedup ), получаемое при использовании параллельного алгоритма для p процессоров, по сравнению с последовательным вариантом выполнения вычислений определяется величиной

Sp(n)=T1(n)/Tp(n),

т.е. как отношение времени решения задач на скалярной ЭВМ к времени выполнения параллельного алгоритма (величина n применяется для параметризации вычислительной сложности решаемой задачи и может пониматься, например, как количество входных данных задачи).

Эффективность ( efficiency ) использования параллельным алгоритмом процессоров при решении задачи определяется соотношением

Ep(n)=T1(n)/(pTp(n))=Sp(n)/p

(величина эффективности определяет среднюю долю времени выполнения алгоритма, в течение которой процессоры реально задействованы для решения задачи).

Из приведенных соотношений можно показать, что в наилучшем случае S_p(n)=p и E_p(n)=1. При практическом применении данных показателей для оценки эффективности параллельных вычислений следует учитывать два важных момента:

• При определенных обстоятельствах ускорение может оказаться больше числа используемых процессоров S_p(n)>p - в этом случае говорят о существовании сверхлинейного (superlinear) ускорения. Несмотря на парадоксальность таких ситуаций ( ускорение превышает число процессоров), на практике сверхлинейное ускорение может иметь место. Одной из причин такого явления может быть неодинаковость условий выполнения последовательной и параллельной программ. Например, при решении задачи на одном процессоре оказывается недостаточно оперативной памяти для хранения всех обрабатываемых данных и тогда становится необходимым использование более медленной внешней памяти (в случае же использования нескольких процессоров оперативной памяти может оказаться достаточно за счет разделения данных между процессорами). Еще одной причиной сверхлинейного ускорения может быть нелинейный характер зависимости сложности решения задачи от объема обрабатываемых данных. Так, например, известный алгоритм пузырьковой сортировки характеризуется квадратичной зависимостью количества необходимых операций от числа упорядочиваемых данных. Как результат, при распределении сортируемого массива между процессорами может быть получено ускорение, превышающее число процессоров (более подробно данный пример рассматривается в "Параллельные методы сортировки" ). Источником сверхлинейного ускорения может быть и различие вычислительных схем последовательного и параллельного методов,
• При внимательном рассмотрении можно обратить внимание, что попытки повышения качества параллельных вычислений по одному из показателей (ускорению или эффективности) могут привести к ухудшению ситуации по другому показателю, ибо показатели качества параллельных вычислений являются часто противоречивыми. Так, например, повышение ускорения обычно может быть обеспечено за счет увеличения числа процессоров, что приводит, как правило, к падению эффективности. И наоборот, повышение эффективности достигается во многих случаях при уменьшении числа процессоров (в предельном случае идеальная эффективность E_p(n)=1 легко обеспечивается при использовании одного процессора). Как результат, разработка методов параллельных вычислений часто предполагает выбор некоторого компромиссного варианта с учетом желаемых показателей ускорения и эффективности.

При выборе надлежащего параллельного способа решения задачи может оказаться полезной оценка стоимости (cost) вычислений, определяемой как произведение времени параллельного решения задачи и числа используемых процессоров

Cp=pTp.

В связи с этим можно определить понятие стоимостно-оптимального (cost-optimal) параллельного алгоритма как метода, стоимость которого является пропорциональной времени выполнения наилучшего последовательного алгоритма.

Далее для иллюстрации введенных понятий в следующем пункте будет рассмотрен учебный пример решения задачи вычисления частных сумм для последовательности числовых значений. Кроме того, данные показатели будут использоваться для характеристики эффективности всех рассматриваемых в лекциях 6 – 11 параллельных алгоритмов при решении ряда типовых задач вычислительной математики.

2.5. Учебный пример. Вычисление частных сумм последовательности числовых значений

Рассмотрим для демонстрации ряда проблем, возникающих при разработке параллельных методов вычислений, сравнительно простую задачу нахождения частных сумм последовательности числовых значений

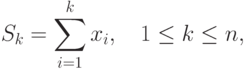
Изучение возможных параллельных методов решения данной задачи начнем с еще более простого варианта ее постановки – с задачи вычисления общей суммы имеющегося набора значений (в таком виде задача суммирования является частным случаем общей задачи редукции )

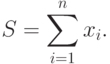
2.5.1. Последовательный алгоритм суммирования

Традиционный алгоритм для решения этой задачи состоит в последовательном суммировании элементов числового набора

S=0,
S=S+x1,...

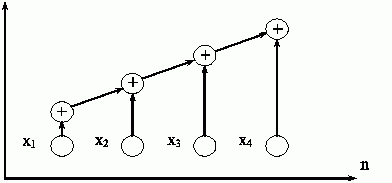
Вычислительная схема данного алгоритма может быть представлена следующим образом (см. рис. 2.2):

G1=(V1,R1),

где V₁={v₀₁,...,v_0n, v₁₁,...,v_1n} есть множество операций (вершины v₀₁,...,v_0n обозначают операции ввода, каждая вершина v_1i, 1<=i<=n, соответствует прибавлению значения x_i к накапливаемой сумме S ), а

R1={(v0i,v1i),(v1i,v1i+1), 1<=i<=n–1}

есть множество дуг, определяющих информационные зависимости операций.

Рис. 2.2. Последовательная вычислительная схема алгоритма суммирования

Как можно заметить, данный "стандартный" алгоритм суммирования допускает только строго последовательное исполнение и не может быть распараллелен.

2.5.2. Каскадная схема суммирования

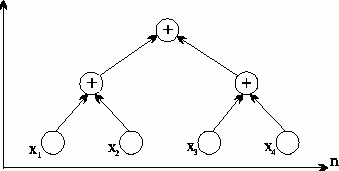
Параллелизм алгоритма суммирования становится возможным только при ином способе построения процесса вычислений, основанном на использовании ассоциативности операции сложения. Получаемый новый вариант суммирования (известный в литературе как каскадная схема ) состоит в следующем (см. рис. 2.3):

• на первой итерации каскадной схемы все исходные данные разбиваются на пары, и для каждой пары вычисляется сумма их значений;
• далее все полученные суммы также разбиваются на пары, и снова выполняется суммирование значений пар и т.д.

Данная вычислительная схема может быть определена как граф (пусть n=2^k )

G2(V2,R2),

Рис. 2.3. Каскадная схема алгоритма суммирования

где V₂={(v_i1,...,v_li), 0<=i<=k, 1<=l_i<=2^-1n} есть вершины графа ( (v₀₁,...v_0n) - операции ввода, (v_1l,...,v_1n/2) - операции суммирования первой итерации и т.д.), а множество дуг графа определяется соотношениями:

R2={(vi-1,2j-1vij),(vi-1,2jvij), 1<=i<=k, 1<=j<=2-in}.

Как нетрудно оценить, количество итераций каскадной схемы оказывается равным величине

k=log2n,

а общее количество операций суммирования

Kпосл=n/2+n/4+...+1=n–1

совпадает с количеством операций последовательного варианта алгоритма суммирования. При параллельном исполнении отдельных итераций каскадной схемы общее количество параллельных операций суммирования является равным

Kпар=log2n.

Поскольку считается, что время выполнения любых вычислительных операций является одинаковым и единичным, то T₁=K_посл, T_p=K_пар, поэтому показатели ускорения и эффективности каскадной схемы алгоритма суммирования можно оценить как

Sp=T1/Tp=(n–1)/log2n,
Ep=T1/pTp=(n–1)/(plog2n)=(n–1)/((n/2)log2n),

где p=n/2 есть необходимое для выполнения каскадной схемы количество процессоров.

Анализируя полученные характеристики, можно отметить, что время параллельного выполнения каскадной схемы совпадает с оценкой для паракомпьютера в теореме 2. Однако при этом эффективность использования процессоров уменьшается при увеличении количества суммируемых значений