Моделирование и анализ параллельных вычислений

2.10. Контрольные вопросы

1. Как определяется модель "операции — операнды"?
2. Как определяется расписание для распределения вычислений между процессорами?
3. Как определяется время выполнения параллельного алгоритма?
4. Какое расписание является оптимальным?
5. Как определить минимально возможное время решения задачи?
6. Что понимается под паракомпьютером и для чего может оказаться полезным данное понятие?
7. Какие оценки следует использовать в качестве характеристики времени последовательного решения задачи?
8. Как определить минимально возможное время параллельного решения задачи по графу "операнды – операции"?
9. Какие зависимости могут быть получены для времени параллельного решения задачи при увеличении или уменьшении числа используемых процессоров?
10. При каком числе процессоров могут быть получены времена выполнения параллельного алгоритма, сопоставимые по порядку с оценками минимально возможного времени решения задачи?
11. Как определяются понятия ускорения и эффективности?
12. Возможно ли достижение сверхлинейного ускорения?
13. В чем состоит противоречивость показателей ускорения и эффективности?
14. Как определяется понятие стоимости вычислений?
15. В чем состоит понятие стоимостно-оптимального алгоритма?
16. В чем заключается проблема распараллеливания последовательного алгоритма суммирования числовых значений?
17. В чем состоит каскадная схема суммирования? С какой целью рассматривается модифицированный вариант данной схемы?
18. В чем состоит различие показателей ускорения и эффективности для рассматриваемых вариантов каскадной схемы суммирования?
19. В чем состоит параллельный алгоритм вычисления всех частных сумм последовательности числовых значений?
20. Как формулируется закон Амдаля? Какой аспект параллельных вычислений позволяет учесть данный закон?
21. Какие предположения используются для обоснования закона Густавсона – Барсиса?
22. Как определяется функция изоэффективности?
23. Какой алгоритм является масштабируемым? Приведите примеры методов с разным уровнем масштабируемости.

2.11. Задачи и упражнения

1. Разработайте модель и выполните оценку показателей ускорения и эффективности параллельных вычислений:

• для задачи скалярного произведения двух векторов
  
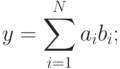
• для задачи поиска максимального и минимального значений для заданного набора числовых данных
  
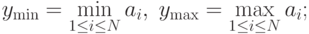
• для задачи нахождения среднего значения для заданного набора числовых данных
  

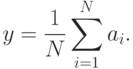
2. Выполните в соответствии с законом Амдаля оценку максимально достижимого ускорения для задач п. 1.

3. Выполните оценку ускорения масштабирования для задач п.1.

4. Выполните построение функций изоэффективности для задач п.1.

5. Разработайте модель и выполните полный анализ эффективности параллельных вычислений ( ускорение, эффективность, максимально достижимое ускорение, ускорение масштабирования, функция изоэффективности ) для задачи умножения матрицы на вектор.