Моделирование и анализ параллельных вычислений
2.3. Определение времени выполнения параллельного алгоритма
Вычислительная схема алгоритма G совместно с расписанием Hp может рассматриваться как модель параллельного алгоритма Ap(G,Hp), исполняемого с использованием p процессоров. Время выполнения параллельного алгоритма определяется максимальным значением времени, применяемым в расписании
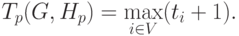
Для выбранной схемы вычислений желательно использование расписания, обеспечивающего минимальное время исполнения алгоритма
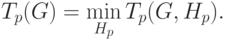
Уменьшение времени выполнения может быть обеспечено и путем подбора наилучшей вычислительной схемы
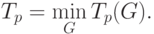
Оценки Tp(G,Hp), Tp(G) и Tp могут быть применены в качестве показателей времени выполнения параллельного алгоритма. Кроме того, для анализа максимально возможного параллелизма можно определить оценку наиболее быстрого исполнения алгоритма

Оценку 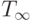 можно рассматривать
как минимально возможное время выполнения параллельного алгоритма
при использовании неограниченного количества процессоров
(концепция вычислительной системы с бесконечным количеством
процессоров, обычно называемой паракомпьютером, широко
применяется при теоретическом анализе параллельных вычислений).
можно рассматривать
как минимально возможное время выполнения параллельного алгоритма
при использовании неограниченного количества процессоров
(концепция вычислительной системы с бесконечным количеством
процессоров, обычно называемой паракомпьютером, широко
применяется при теоретическом анализе параллельных вычислений).
Оценка T1 определяет время выполнения алгоритма при использовании одного процессора и представляет, тем самым, время выполнения последовательного варианта алгоритма решения задачи. Построение подобной оценки является важной задачей при анализе параллельных алгоритмов, поскольку она необходима для определения эффекта использования параллелизма (ускорения времени решения задачи). Очевидно, что
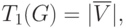
 , напомним, есть количество вершин
вычислительной схемы без вершин ввода. Важно отметить, что если
при определении оценки ограничиться рассмотрением только одного
выбранного алгоритма решения задачи и использовать величину
, напомним, есть количество вершин
вычислительной схемы без вершин ввода. Важно отметить, что если
при определении оценки ограничиться рассмотрением только одного
выбранного алгоритма решения задачи и использовать величину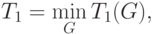

Приведем без доказательства теоретические положения, характеризующие свойства оценок времени выполнения параллельного алгоритма (см. [22]).
Теорема 1. Минимально возможное время выполнения параллельного алгоритма определяется длиной максимального пути вычислительной схемы алгоритма, т.е.

Теорема 2. Пусть для некоторой вершины вывода в вычислительной схеме алгоритма существует путь из каждой вершины ввода. Кроме того, пусть входная степень вершин схемы (количество входящих дуг) не превышает 2. Тогда минимально возможное время выполнения параллельного алгоритма ограничено снизу значением
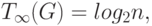
где n есть количество вершин ввода в схеме алгоритма.
Теорема 3. При уменьшении числа используемых процессоров время выполнения алгоритма увеличивается пропорционально величине уменьшения количества процессоров, т.е.
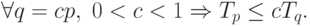
Теорема 4. Для любого количества используемых процессоров справедлива следующая верхняя оценка для времени выполнения параллельного алгоритма
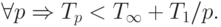
Теорема 5. Времени выполнения алгоритма, которое
сопоставимо с минимально возможным временем 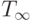 , можно достичь при количестве
процессоров порядка
, можно достичь при количестве
процессоров порядка 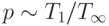 ,
а именно,
,
а именно,

При меньшем количестве процессоров время выполнения алгоритма не может превышать более чем в 2 раза наилучшее время вычислений при имеющемся числе процессоров, т.е.
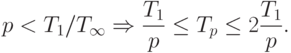
Приведенные утверждения позволяют дать следующие рекомендации по правилам формирования параллельных алгоритмов:
- при выборе вычислительной схемы алгоритма должен использоваться граф с минимально возможным диаметром (см. теорему 1);
- для параллельного выполнения целесообразное количество
процессоров определяется величиной
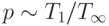 (см. теорему 5);
(см. теорему 5); - время выполнения параллельного алгоритма ограничивается сверху величинами, приведенными в теоремах 4 и 5.
Для вывода рекомендаций по формированию расписания по параллельному выполнению алгоритма приведем доказательство теоремы 4.
Доказательство теоремы 4. Пусть 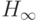 есть расписание для достижения минимально возможного времени
выполнения
есть расписание для достижения минимально возможного времени
выполнения 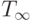 . Для каждой итерации
. Для каждой итерации 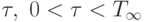 , выполнения
расписания
, выполнения
расписания 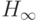 обозначим через
обозначим через 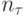 количество операций, выполняемых в
ходе итерации
количество операций, выполняемых в
ходе итерации 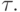 Расписание выполнения алгоритма
с использованием p процессоров может быть построено
следующим образом. Выполнение алгоритма разделим на
Расписание выполнения алгоритма
с использованием p процессоров может быть построено
следующим образом. Выполнение алгоритма разделим на 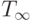 шагов; на каждом шаге
шагов; на каждом шаге  следует выполнить все
следует выполнить все 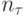 операций, которые выполнялись на итерации
операций, которые выполнялись на итерации  расписания
расписания 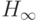 . Эти операции могут быть выполнены не
более чем за
. Эти операции могут быть выполнены не
более чем за 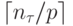 итераций
при использовании p процессоров. Как результат, время
выполнения алгоритма Tp может быть оценено
следующим образом
итераций
при использовании p процессоров. Как результат, время
выполнения алгоритма Tp может быть оценено
следующим образом

Доказательство теоремы дает практический способ построения расписания параллельного алгоритма. Первоначально может быть построено расписание без учета ограниченности числа используемых процессоров ( расписание для паракомпьютера ). Затем, согласно схеме вывода теоремы, может быть построено расписание для конкретного количества процессоров.
