Моделирование и анализ параллельных вычислений
2.7. Анализ масштабируемости параллельных вычислений
Целью применения параллельных вычислений во многих случаях является не только уменьшение времени выполнения расчетов, но и обеспечение возможности решения более сложных вариантов задач (таких постановок, решение которых не представляется возможным при использовании однопроцессорных вычислительных систем). Способность параллельного алгоритма эффективно использовать процессоры при повышении сложности вычислений является важной характеристикой выполняемых расчетов. Поэтому параллельный алгоритм называют масштабируемым ( scalable ), если при росте числа процессоров он обеспечивает увеличение ускорения при сохранении постоянного уровня эффективности использования процессоров. Возможный способ характеристики свойств масштабируемости состоит в следующем.
Оценим накладные расходы ( total overhead ), которые имеют место при выполнении параллельного алгоритма
T0=pTp–T1.
Накладные расходы появляются за счет необходимости организации взаимодействия процессоров, выполнения некоторых дополнительных действий, синхронизации параллельных вычислений и т.п. Используя введенное обозначение, можно получить новые выражения для времени параллельного решения задачи и соответствующего ускорения:
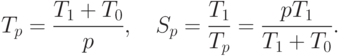
Применяя полученные соотношения, эффективность использования процессоров можно выразить как
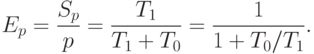
Последнее выражение показывает, что если сложность решаемой задачи является фиксированной ( T1=const ), то при росте числа процессоров эффективность, как правило, будет убывать за счет роста накладных расходов T0. При фиксации числа процессоров эффективность их использования можно улучшить путем повышения сложности решаемой задачи T1 (предполагается, что при росте параметра сложности n накладные расходы T0 увеличиваются медленнее, чем объем вычислений T1 ). Как результат, при увеличении числа процессоров в большинстве случаев можно обеспечить определенный уровень эффективности при помощи соответствующего повышения сложности решаемых задач. Поэтому важной характеристикой параллельных вычислений становится соотношение необходимых темпов роста сложности расчетов и числа используемых процессоров.
Пусть E=const есть желаемый уровень эффективности выполняемых вычислений. Из выражения для эффективности можно получить

Порождаемую последним соотношением зависимость n=F(p) между сложностью решаемой задачи и числом процессоров обычно называют функцией изоэффективности ( isoefficiency function ) (см. [51]).
Покажем в качестве иллюстрации вывод функции изоэффективности для учебного примера суммирования числовых значений. В этом случае

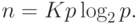
Как результат, например, при числе процессоров p=16 для обеспечения уровня эффективности E=0,5 (т.е. K=1 ) количество суммируемых значений должно быть не менее n=64. Или же, при увеличении числа процессоров с p до q (q>p) для обеспечения пропорционального роста ускорения (Sq/Sp)=(q/p) необходимо увеличить число суммируемых значений n в (qlog2q)/(plog2p) раз.
2.8. Краткий обзор лекции
В лекции рассматривается модель вычислений в виде графа "операции – операнды", которая может использоваться для описания существующих информационных зависимостей в выбираемых алгоритмах решения задач.
В основу данной модели положен ациклический ориентированный граф, в котором вершины представляют операции, а дуги соответствуют зависимостям операций по данным. При наличии такого графа для определения параллельного алгоритма достаточно задать расписание, в соответствии с которым фиксируется распределение выполняемых операций по процессорам.
Представление вычислений при помощи моделей подобного вида позволяет получить аналитически ряд характеристик разрабатываемых параллельных алгоритмов, среди которых время выполнения, схема оптимального расписания, оценки максимально возможного быстродействия методов решения поставленных задач. Для более простого построения теоретических оценок в лекции рассматривается понятие паракомпьютера как параллельной системы с неограниченным количеством процессоров.
Для оценки оптимальности разрабатываемых методов параллельных вычислений в лекции приводятся широко используемые в теории и практике параллельного программирования основные показатели качества - ускорение ( speedup ), показывающее, во сколько раз быстрее осуществляется решение задач при использовании нескольких процессоров, и эффективность ( efficiency ), которая характеризует долю времени реального использования процессоров вычислительной системы. Важной характеристикой разрабатываемых алгоритмов является стоимость ( cost ) вычислений, определяемая как произведение времени параллельного решения задачи и числа используемых процессоров.
Для демонстрации применимости рассмотренных моделей и методов анализа параллельных алгоритмов в лекции рассматривается задача нахождения частных сумм последовательности числовых значений. На данном примере отмечается проблема сложности распараллеливания последовательных алгоритмов, которые изначально не были ориентированы на возможность организации параллельных вычислений. Для выделения "скрытого" параллелизма показывается возможность преобразования исходной последовательной схемы вычислений и приводится получаемая в результате таких преобразований каскадная схема. На примере этой же задачи отмечается возможность введения избыточных вычислений для достижения большего параллелизма выполняемых расчетов.
В завершение лекции рассматривается вопрос построения оценок максимально достижимых значений показателей эффективности. Для получения таких оценок может быть использован закон Амдаля ( Amdahl ), позволяющий учесть существование последовательных (нераспараллеливаемых) вычислений в методах решения задач. Закон Густавсона – Барсиса ( Gustafson – Barsis's law ) обеспечивает построение оценок ускорения масштабирования ( scaled speedup ), применяемое для характеристики того, насколько эффективно могут быть организованы параллельные вычисления при увеличении сложности решаемых задач. Для определения зависимости между сложностью решаемой задачи и числом процессоров, при соблюдении которой обеспечивается необходимый уровень эффективности параллельных вычислений, вводится понятие функции изоэффективности ( isoefficiency function ).
2.9. Обзор литературы
Дополнительная информация по моделированию и анализу параллельных вычислений может быть получена, например, в [2, 22]), полезная информация содержится также в [51, 63].
Рассмотрение учебной задачи суммирования последовательности числовых значений было выполнено в [22].
Впервые закон Амдаля был изложен в работе [18]. Закон Густавсона – Барсиса был опубликован в работе [43]. Понятие функции изоэффективности было предложено в работе [39].
Систематическое изложение (на момент издания работы) вопросов моделирования и анализа параллельных вычислений приводится в [77].
