НОУ ИНТУИТ | Основы теории вычислимых функций. Лекция 8: Арифметическая иерархия

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 16.03.2007 | Доступ: свободный | Студентов: 532 / 43 | Оценка: 4.45 / 4.18 | Длительность: 15:50:00

Теги: beta, алгоритмы, всюду определенные функции, вычисления, вычислимость, вычислительная модель, графика, дополнение множества, одноместная функция, полугруппа, примитивная рекурсия, примитивно рекурсивная функция, процедуры, разрешимые множества, теория, универсальное множество, частично рекурсивная функция, элементы, эффективность

|

Вам нравится? Нравится 5 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Посвящена критериям принадлежности свойств классам свойств, определяющихся последовательностями дескрипторов – кванторов существования и общности, свойствам пересечений, объединений, дополнений множеств из этих классов.

Классы Sigma _n и Pi _n

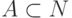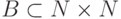Мы уже говорили, что перечислимые множества можно эквивалентно определить как проекции разрешимых множеств: множество $A \subset N$ перечислимо тогда и только тогда, когда существует разрешимое множество $B \subset N \times N$ , проекцией которого оно является. Если отождествлять множества со свойствами, то можно сказать, что свойство A(x) натуральных чисел перечислимо тогда и только тогда, когда его можно представить в виде

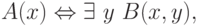
$A(x) \Leftrightarrow \exists\ y\ B(x,y),$

где B(x,y) некоторое разрешимое свойство.

(В этом разделе мы предполагаем знакомство читателя с простейшими логическими обозначениями: квантор 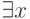$\exists x$ читается как " существует x ", квантор 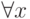$\forall x$ читается как " для всех x ", знак 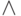$\wedge$ читается как " и" и называется конъюнкцией, знак 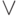$\vee$ читается как " или" и называется дизъюнкцией, знак 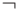$\neg$ читается как " неверно, что" и называется отрицанием. Как и раньше, знак $\Leftrightarrow$ означает равносильность.)

Возникает естественный вопрос: что можно сказать про другие наборы кванторов? Например, какие свойства представимы в виде

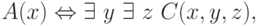
$A(x) \Leftrightarrow \exists\ y\ \exists\ z\ C(x,y,z),$

где C разрешимое свойство троек натуральных чисел? Легко сообразить, что это по-прежнему перечислимые множества. В самом деле, два подряд идущих квантора одного вида можно заменить одним, использовав вычислимую нумерацию пар (которую мы обозначаем квадратными скобками): свойство C', для которого $C'(x,[y,z]) \Leftrightarrow C(x,y,z)$ , также разрешимо, и $A(x) \Leftrightarrow \exists\ w\ C'(x,w)$ .

Другой вопрос: какие свойства представимы в виде

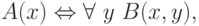
$A(x) \Leftrightarrow \forall\ y\ B(x,y),$

где B(x,y) некоторое разрешимое свойство? Ответ: те, отрицания которых перечислимы (как иногда говорят, коперечислимые ). В самом деле, переходя к отрицаниям, имеем

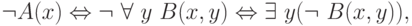
$\neg A(x) \Leftrightarrow \neg\ \forall\ y\ B(x,y) \Leftrightarrow \exists\ y (\neg\ B(x,y)),$

а разрешимые свойства остаются разрешимыми при переходе к отрицаниям.

Дадим общее определение. Свойство A принадлежит классу $\Sigma _{n}$ , если его можно представить в виде

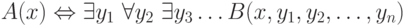
$A(x) \Leftrightarrow \exists y_{1}\ \forall y_{2}\ \exists y_{3} \dots B(x,y_{1},y_{2}, \dots ,y_{n})$

(в правой части стоит n чередующихся кванторов) для некоторого разрешимого свойства B. Если в правой части поставить n чередующихся кванторов, начиная с квантора всеобщности 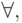$\forall,$ то получится определение класса $\Pi _{n}$ .

Отметим два свойства, которые мы по существу уже доказали:

Теорема 51. (а) Определение класса $\Sigma _{n}$ [ $\Pi _{n}$ ] не изменится, если в правой части разрешить большее число кванторов и требовать, чтобы первый квантор был квантором существования [всеобщности] и число групп одинаковых стоящих рядом кванторов равнялось n. (б) Отрицания свойств из класса $\Sigma _{n}$ принадлежат классу $\Pi _{n}$ и наоборот.

Для доказательства первого утверждения достаточно соединять рядом стоящие одинаковые кванторы с помощью нумерации пар. Для доказательства второго надо проносить отрицание внутрь (меняя тип квантора), пока оно не окажется у разрешимого свойства (где оно роли не играет).

Мы говорили о свойствах; на языке множеств можно сказать так: множества класса $\Sigma _{n}$ получаются из разрешимых с помощью последовательности операций " проекция-дополнение-проекция-дополнение-...-проекция", в которой всего n операций проекции. Каждая операция проекции уменьшает размерность множества (число аргументов у свойства) на единицу, так что начинать надо с разрешимых подмножеств Nⁿ⁺¹.

Теорема 52. Пересечение и объединение двух множеств из класса $\Sigma _{n}$ принадлежит $\Sigma _{n}$ . Пересечение и объединение двух множеств из класса $\Pi _{n}$ принадлежит $\Pi _{n}$ .

Удобно выразить это утверждение на логическом языке, сказав, что конъюнкция и дизъюнкция любых двух свойств из класса $\Sigma _{n}$ лежат в том же классе (аналогично для $\Pi _{n}$ ). На этом же языке удобно провести и доказательство: если, скажем,

$A(x) \Leftrightarrow \exists\ y\ \forall\ z\ B(x,y,z), \\ C(x) \Leftrightarrow \exists\ u \forall\ v\ D(x,u,v), \\ то \\ A(x) \wedge C(x) \Leftrightarrow \exists\ y \exists\ u \forall\ z \forall\ v\ [B(x,y,z) \wedge D(x,u,v)],$

записанное в квадратных скобках свойство разрешимо и остается только соединить пары кванторов в один, как объяснялось выше. Аналогично можно действовать для классов $\Sigma _{n}$ и $\Pi _{n}$ при произвольном n.

Мы определяли классы $\Sigma _{n}$ и $\Pi _{n}$ для множеств натуральных чисел; аналогичным образом это можно сделать и для множеств пар натуральных чисел, троек и вообще любых " конструктивных объектов". Заметим, что проекция множества пар, принадлежащего классу $\Sigma _{n}$ , также принадлежит $\Sigma _{n}$ (поскольку два квантора существования в начале можно объединить в один).

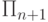Добавляя фиктивные кванторы, легко убедиться, что каждый из двух классов $\Sigma _{n}$ и $\Pi _{n}$ содержится в каждом из классов $\Sigma _{n+1}$ и $\Pi _{n+1}$ . Можно написать еще так:

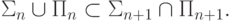
$\Sigma _{n} \cup \Pi _{n} \subset \Sigma _{n+1} \cap \Pi _{n+1}.$

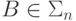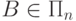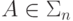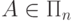Теорема 53. Классы $\Sigma _{n}$ и $\Pi _{n}$ " наследственны вниз" относительно m -сводимости: если A <=_m B и $B \in \Sigma _{n}$ [ $B \in \Pi _{n}$ ], то и $A \in \Sigma _{n}$ [ $A \in \Pi _{n}$ ].

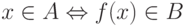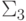В самом деле, пусть A сводится к B с помощью всюду определенной вычислимой функции f, то есть $x \in A \Leftrightarrow f(x) \in B$ . Пусть B принадлежит, например, классу $\Sigma _{3}$ , то есть

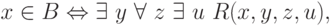
$x \in B \Leftrightarrow \exists\ y\ \forall\ z\ \exists\ u\ R(x,y,z,u),$

где R некоторое разрешимое свойство. Тогда

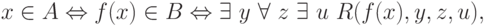
$x \in A \Leftrightarrow f(x) \in B \Leftrightarrow \exists\ y\ \forall\ z\ \exists\ u\ R(f(x),y,z,u),$

и осталось заметить, что R(f(x),y,z,u) (как свойство четверки 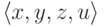$\langle x,y,z,u\rangle$ ) разрешимо.

63. Докажите, что если множество A принадлежит классу $\Sigma _{n}$ , то множество A x A также принадлежит этому классу.

64. Докажите, что если множества A и B принадлежат классу $\Sigma _{n}$ , то их разность A \ B принадлежит классу $\Sigma _{n+1} \cap \Pi _{n+1}$ .

Дальше >>

Авторизоваться

Основы теории вычислимых функций

Арифметическая иерархия

Классы Sigma _n и Pi _n

Вопросы и ответы