Арифметическая иерархия
Универсальные множества вSigma _n и Pi _n
До сих пор мы не показали, что классы  и
и  действительно различаются при разных n. Чтобы показать это,
убедимся, что в каждом из этих классов имеется универсальное
множество (для соответствующего класса) и что оно не принадлежит
меньшим классам.
действительно различаются при разных n. Чтобы показать это,
убедимся, что в каждом из этих классов имеется универсальное
множество (для соответствующего класса) и что оно не принадлежит
меньшим классам.
Теорема 54. Для любого n в классе  существует множество,
универсальное для всех множеств класса
существует множество,
универсальное для всех множеств класса  . (Его
дополнение будет универсальным в классе
. (Его
дополнение будет универсальным в классе  .)
.)
Говоря об универсальном множестве из класса  , мы имеем
в виду множество пар натуральных чисел,
которое принадлежит классу
, мы имеем
в виду множество пар натуральных чисел,
которое принадлежит классу  и
среди сечений которого встречаются все множества натуральных
чисел, принадлежащие классу
и
среди сечений которого встречаются все множества натуральных
чисел, принадлежащие классу  .
.
Для класса 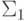 (перечислимых множеств) существование универсального множества мы уже обсуждали. С его помощью можно
построить универсальные множества и для более высоких классов
иерархии. (Начинать надо с первого уровня, так как на "
нулевом" уровне не существует универсального разрешимого
множества.)
(перечислимых множеств) существование универсального множества мы уже обсуждали. С его помощью можно
построить универсальные множества и для более высоких классов
иерархии. (Начинать надо с первого уровня, так как на "
нулевом" уровне не существует универсального разрешимого
множества.)
По определению свойства класса 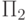 имеют вид
имеют вид  ,
где R некоторое разрешимое свойство. Но их
можно эквивалентно определить и как свойства вида
,
где R некоторое разрешимое свойство. Но их
можно эквивалентно определить и как свойства вида 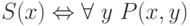 ,
где P некоторое перечислимое свойство. Теперь уже видно,
как построить универсальное множество класса
,
где P некоторое перечислимое свойство. Теперь уже видно,
как построить универсальное множество класса 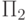 . Возьмем
универсальное перечислимое свойство U(n,x,y), из которого
фиксацией различных n получаются все перечислимые свойства пар
натуральных чисел. Тогда из свойства
. Возьмем
универсальное перечислимое свойство U(n,x,y), из которого
фиксацией различных n получаются все перечислимые свойства пар
натуральных чисел. Тогда из свойства 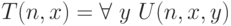 при различных натуральных n получаются все
при различных натуральных n получаются все 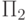 -свойства натуральных чисел. С другой стороны, само
свойство T по построению принадлежит
классу
-свойства натуральных чисел. С другой стороны, само
свойство T по построению принадлежит
классу 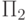 .
.
Дополнение к универсальному 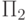 -множеству будет, очевидно,
универсальным
-множеству будет, очевидно,
универсальным 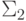 -множеством.
-множеством.
Аналогично можно действовать и для 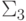 - и
- и 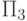 -множеств
(удобнее сначала рассуждать о
-множеств
(удобнее сначала рассуждать о 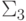 -множествах, так как в
них внутренний квантор является квантором существования и задает
перечислимое множество), и вообще для
-множествах, так как в
них внутренний квантор является квантором существования и задает
перечислимое множество), и вообще для  - и
- и  -множеств.
-множеств.
Теорема 55. Универсальное  -множество не принадлежит классу
-множество не принадлежит классу  . Аналогичным образом, универсальное
. Аналогичным образом, универсальное  -множество не принадлежит классу
-множество не принадлежит классу  .
.
Рассмотрим универсальное  -свойство T(m,x). По определению это означает, что среди его сечений (получающихся, если зафиксировать m ) есть все
-свойство T(m,x). По определению это означает, что среди его сечений (получающихся, если зафиксировать m ) есть все  -свойства. Пусть T принадлежит классу
-свойства. Пусть T принадлежит классу  . Тогда его диагональ, свойство D(x)=T(x,x), также лежит в
. Тогда его диагональ, свойство D(x)=T(x,x), также лежит в  (например, потому, что D <=m T ), а ее отрицание, свойство
(например, потому, что D <=m T ), а ее отрицание, свойство 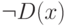 , принадлежит классу
, принадлежит классу  . Но этого не может быть, так как
. Но этого не может быть, так как 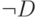 отлично от всех сечений свойства T (оно отличается от m -го сечения в точке m ), а T универсально.
отлично от всех сечений свойства T (оно отличается от m -го сечения в точке m ), а T универсально.
Из этой теоремы следует, в частности, что любой из
классов  и
и  является собственным
подмножеством любого
из классов
является собственным
подмножеством любого
из классов  и
и 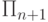 . (Мы увидим
вскоре,
что даже объединение
. (Мы увидим
вскоре,
что даже объединение 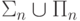 является собственным
подмножеством пересечения
является собственным
подмножеством пересечения  .)
.)
Операция скачка
Мы хотим показать, что класс  совпадает с классом всех A -перечислимых
множеств для некоторого множества A (зависящего от n,
естественно). Чтобы объяснить, что это за множество, нам
понадобится так называемая операция скачка.
совпадает с классом всех A -перечислимых
множеств для некоторого множества A (зависящего от n,
естественно). Чтобы объяснить, что это за множество, нам
понадобится так называемая операция скачка.
Пусть X произвольное множество. Среди X -перечислимых множеств есть универсальное. Это множество будет m -полным в классе X -перечислимых множеств в том смысле, что все другие X -перечислимые множества к нему m -сводятся.
Сводящая
функция, как мы видели, имеет вид x 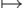 [n,x] (и вычислима
безо всякого оракула, как того и требует определение m -сводимости). Будем обозначать через X' любое m -полное
множество в классе X -перечислимых множеств. Можно сказать,
что X' определено с точностью до m -эквивалентности.
[n,x] (и вычислима
безо всякого оракула, как того и требует определение m -сводимости). Будем обозначать через X' любое m -полное
множество в классе X -перечислимых множеств. Можно сказать,
что X' определено с точностью до m -эквивалентности.
Более формально, будем говорить, что множества P и Q являются m - эквивалентными, если P <=m Q и Q <=m P. (Легко видеть, что это действительно отношение эквивалентности.) Класс эквивалентных множеств называют m - степенью. Таким образом, можно сказать, что мы для каждого множества X определили некоторую m -степень X'.
Аналогичным образом определяют T - степени (которые называют также тьюринговыми степенями или степенями неразрешимости ) как классы T -эквивалентных множеств; множества P и Q называют T - эквивалентными, или эквивалентными по Тьюрингу, если P <=T Q и Q<=T P, то есть если каждое из множеств разрешимо относительно другого. Если множества P и Q эквивалентны по Тьюрингу, то класс P -вычислимых функций совпадает с классом Q -вычислимых функций (а класс P -перечислимых множеств совпадает с классом Q -перечислимых множеств). Введя понятие T -степени, можно сказать, что m -степень X' определяется T -степенью множества X и тем самым определено отображение множества всех T -степеней в множество всех m -степеней. Это отображение называют операцией скачка ; множество (точнее, m -степень) X' называют скачком множества (точнее, T -степени) X.
65. Могут ли при этом отображении разные T -степени переходить в одну и ту же m -степень? нет, так как перечислимые одни и те же и разрешимые тоже
66. Докажите, что любые два m -полных
в классе  множества вычислимо
изоморфны (отличаются вычислимой перестановкой).
множества вычислимо
изоморфны (отличаются вычислимой перестановкой).
67. Покажите, что для любого перечислимого множества A можно
указать такое действительное число 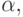 что множество всех
рациональных чисел, меньших
что множество всех
рациональных чисел, меньших 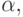 будет перечислимо и
эквивалентно по Тьюрингу множеству A.
будет перечислимо и
эквивалентно по Тьюрингу множеству A.
Обычно, впрочем, операцию скачка рассматривают на T -степенях, считая ее результатом T -степень, содержащую X' (это законно, так как T -классификация более грубая).
Нам понадобятся следующие T -степени: 0 (степень, содержащая все разрешимые множества), 0' (ее скачок, степень m -полного перечислимого неразрешимого множества; мы ее уже рассматривали), затем 0'' (скачок степени 0' ), 0''' и так далее; вообще 0(n+1)= (0(n))'.
Теорема 56. При любом n >= 1 класс  совпадает с
классом всех 0(n-1) -перечислимых множеств.
совпадает с
классом всех 0(n-1) -перечислимых множеств.
(Пока что мы знаем это при n=1.)
Докажем сначала, что все  -множества перечислимы
относительно 0(n-1). Это делается индукцией
по n.
При n=1 это известно. Рассмотрим теперь произвольное
множество X из
-множества перечислимы
относительно 0(n-1). Это делается индукцией
по n.
При n=1 это известно. Рассмотрим теперь произвольное
множество X из 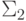 . По определению,
. По определению,
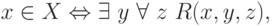
где R разрешимое свойство. Свойство  имеет перечислимое отрицание. Это отрицание разрешимо
относительно 0', так как m -сводится к m -полному
перечислимому множеству. Значит, и само свойство
имеет перечислимое отрицание. Это отрицание разрешимо
относительно 0', так как m -сводится к m -полному
перечислимому множеству. Значит, и само свойство 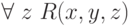 разрешимо относительно 0'. Поэтому его
проекция, множество X, перечислимо
относительно 0'.
разрешимо относительно 0'. Поэтому его
проекция, множество X, перечислимо
относительно 0'.
Аналогично можно рассуждать и для больших n. Если X принадлежит 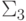 , то
, то
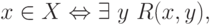
где R принадлежит 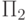 . Отрицание R
принадлежит
. Отрицание R
принадлежит 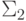 (по доказанному), поэтому 0' -перечислимо,
поэтому 0'' -разрешимо, поэтому само R тоже 0'' -разрешимо, а его проекция 0'' -перечислима.
(по доказанному), поэтому 0' -перечислимо,
поэтому 0'' -разрешимо, поэтому само R тоже 0'' -разрешимо, а его проекция 0'' -перечислима.
Первая половина теоремы доказана.
Для доказательства второй половины нам потребуется некоторое
свойство классов  и
и  . Рассмотрим
какую-нибудь
вычислимую нумерацию всех конечных множеств натуральных чисел. Обозначим через Dx конечное множество номер x. Для
произвольного множества A рассмотрим
множество Subset(A) всех конечных подмножеств A,
точнее, множество всех их номеров:
. Рассмотрим
какую-нибудь
вычислимую нумерацию всех конечных множеств натуральных чисел. Обозначим через Dx конечное множество номер x. Для
произвольного множества A рассмотрим
множество Subset(A) всех конечных подмножеств A,
точнее, множество всех их номеров:
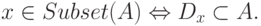
Лемма 1. Если множество A принадлежит
классу  [или
[или  ], то
множество Subset(A) также
принадлежит
классу
], то
множество Subset(A) также
принадлежит
классу  [соответственно
[соответственно  ].
].
(Утверждение этой леммы обобщает сформулированное в задаче 63 утверждение о множестве Ax A: теперь мы рассматриваем не пары, а произвольные кортежи.)
Доказательство леммы. Пусть множество A принадлежит,
например, классу 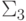 :
:
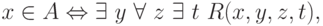
где R разрешимое свойство. Тогда можно записать
свойство 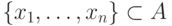 следующим образом:
следующим образом:
![\begin{multiline*}
\exists \langle y_1,\dots,y_n \rangle
\forall \langle z_1,\dots,z_n \rangle
\exists \langle t_1,\dots,t_n \rangle
[R(x_1,y_1,z_1,t_1) \land \ldots \\
\ldots\land R(x_n,y_n,z_n,t_n)]
\end{multiline*}](/sites/default/files/tex_cache/b7685e932a33f4e9b197efe43926827b.png)
Эта формула использует кванторы по кортежам натуральных чисел
(переменной длины), но их можно заменить на номера
этих кортежей в какой-нибудь вычислимой нумерации. При этом
стоящая под кванторами формула (она записана несколько условно:
символическая конъюнкция на самом деле имеет переменную длину)
является разрешимым свойством номеров кортежей,
поэтому вся правая часть является 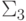 -свойством.
-свойством.
(На самом деле мы допустили еще одну вольность речи: правая
часть является не свойством конечного
множества {x1,...,xn}, а
свойством
кортежа (упорядоченной последовательности) 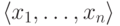 . Но переход от номера множества к номеру
какого-то кортежа, содержащего все его элементы, вычислим,
так что проблемы тут нет.)
. Но переход от номера множества к номеру
какого-то кортежа, содержащего все его элементы, вычислим,
так что проблемы тут нет.)
Лемма доказана.
