Арифметическая иерархия
68. Докажите, что
если A принадлежит
классу  [
[  ], то и
множество
], то и
множество  номеров конечных множеств,
пересекающихся с A, принадлежит классу
номеров конечных множеств,
пересекающихся с A, принадлежит классу  [
[  ].
].
69. Пусть свойство R(x,y) пар натуральных чисел принадлежит классу  . Покажите, что свойство
. Покажите, что свойство
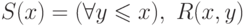
принадлежит  . (Ограниченный квантор
. (Ограниченный квантор 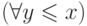 читается как " для всех y, не превосходящих x ".)
читается как " для всех y, не превосходящих x ".)
Переходя к дополнениям, мы немедленно получаем такое утверждение:
Лемма 2. Если A принадлежит
классу  [
[  ],
то множество Disjoint(A), состоящее из номеров конечных
множеств, не пересекающихся с A,
принадлежит
],
то множество Disjoint(A), состоящее из номеров конечных
множеств, не пересекающихся с A,
принадлежит  [
[  ].
].
Доказательство леммы. Не пересекаться с A означает быть
подмножеством дополнения к A, и остается воспользоваться
предыдущей леммой и тем, что дополнение к множеству из
класса  [
[  ] лежит в
классе
] лежит в
классе  [
[  ].
Лемма доказана.
].
Лемма доказана.
Теперь мы можем перейти к доказательству того факта, что все
множества, перечислимые относительно 0(n-1),
принадлежат классу  . Это также доказывается индукцией
по n.
. Это также доказывается индукцией
по n.
Начнем с первого нетривиального случая: почему множество,
перечислимое относительно 0', лежит в 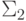 ?
(Здесь можно было бы применить критерий 0' -вычислимости, приведенный выше, но мы предпочитаем
действовать по общей схеме, которая годится и для
больших n.)
?
(Здесь можно было бы применить критерий 0' -вычислимости, приведенный выше, но мы предпочитаем
действовать по общей схеме, которая годится и для
больших n.)
Итак, пусть некоторое множество A перечислимо относительно 0'. Тогда оно перечислимо относительно некоторого перечислимого множества B, то есть перечислимо относительно характеристической функции b множества B. Согласно доказанному нами выше критерию (теорема 45), это означает, что существует перечислимое множество Q пар вида 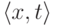 , где x число, а t образец, для которого
, где x число, а t образец, для которого
![x \in A \Leftrightarrow
\exists t [\text{($\langle x,t\rangle \in Q$)
и ($b$~продолжает~$t$)}].](/sites/default/files/tex_cache/0ac04e50b7e5ddd0ca866e8cfe318d69.png)
Без ограничения общности можно считать, что образец t представляет собой функцию, определенную на конечном множестве и принимающую значения 0 и 1. (Если у t есть какие-то другие значения, то он не может быть частью характеристической функции множества B и роли не играет.) Условие " b продолжает t " в терминах множества B звучит так: B содержит множество тех аргументов, на которых t принимает значение 1, и не пересекается с множеством тех аргументов, на которых t принимает значение 0. Поэтому вместо образцов можно говорить о парах конечных множеств; тогда вместо Q надо рассмотреть перечислимое множество P троек вида 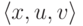 и написать так:
и написать так:
![\begin{multiline*}
x \in A \Leftrightarrow
\exists u\exists v [\text{($\langle x,u,v\rangle \in P$)
и ($D_u$~содержится в~$B$)}\\
\text{и ($D_v$~не пересекается с~$B$)}].
\end{multiline*}](/sites/default/files/tex_cache/4ee21b668dfa00ba82bbb3ccf7153852.png)
Теперь вместо " Du содержится в B " напишем " 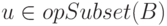 ", а вместо " Dv не пересекается с B " напишем "
", а вместо " Dv не пересекается с B " напишем " 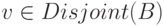 ". Остается заметить, что все три свойства, соединенные союзом " и" в правой части, принадлежат классу
". Остается заметить, что все три свойства, соединенные союзом " и" в правой части, принадлежат классу 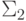 и даже меньшим классам. Именно, первые два принадлежат классу
и даже меньшим классам. Именно, первые два принадлежат классу 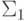 , так как P и B перечислимы (для второго свойства применяем лемму 1). Третье же принадлежит классу
, так как P и B перечислимы (для второго свойства применяем лемму 1). Третье же принадлежит классу  по лемме 2. Поэтому их конъюнкция принадлежит классу
по лемме 2. Поэтому их конъюнкция принадлежит классу 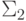 , и операция проекции (кванторы
, и операция проекции (кванторы 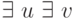 ) не выводит за пределы этого класса. Случай n=2 разобран.
) не выводит за пределы этого класса. Случай n=2 разобран.
Далее, если какое-то множество A перечислимо относительно 0'', то по определению это означает, что оно перечислимо относительно некоторого B, которое перечислимо относительно 0' и потому лежит в 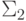 . После этого все рассуждения проходят точно так же со сдвигом на 1. Аналогично разбираются и все следующие значения n.
. После этого все рассуждения проходят точно так же со сдвигом на 1. Аналогично разбираются и все следующие значения n.
Из доказанной теоремы немедленно вытекает такое следствие:
Теорема 57. Пересечение классов  совпадает с классом разрешимых относительно 0(n-1) множеств.
совпадает с классом разрешимых относительно 0(n-1) множеств.
В самом деле, релятивизованная теорема Поста (теорема 2) утверждает, что некоторое множество является X -разрешимым тогда и только тогда, когда оно и его дополнение X -перечислимы (здесь X произвольный оракул).
Теорема 58. Класс 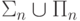 является собственным подмножеством класса
является собственным подмножеством класса  .
.
Вспомним, что такое 0(n). Это степень множества X, являющегося m -полным в классе 0(n-1) -перечислимых множеств. Поскольку X является m -полным в указанном классе, оно не 0(n-1) -разрешимо, то есть его дополнение не является 0(n-1) -перечислимым.
Значит, по доказанной только что теореме X принадлежит классу  , а его дополнение нет. Напротив, дополнение к X принадлежит
, а его дополнение нет. Напротив, дополнение к X принадлежит  , но не
, но не  . Рассмотрим теперь " соединение" множества X с его дополнением, е множество
. Рассмотрим теперь " соединение" множества X с его дополнением, е множество
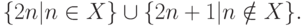
К этому множеству m -сводятся как X, так и его дополнение, поэтому оно не может принадлежать ни  , ни
, ни  . С другой стороны, оно, очевидно, разрешимо относительно X, поэтому по доказанной теореме принадлежит и
. С другой стороны, оно, очевидно, разрешимо относительно X, поэтому по доказанной теореме принадлежит и  , и
, и 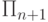 .
.
