Рекурсивные функции
Примитивно рекурсивные функции
Программы с конечным числом переменных напоминали ассемблер; рассматриваемые в этом разделе рекурсивные функции скорее напоминают функциональное программирование, когда одни функции определяются через другие. Мы будем рассматривать функции с натуральными аргументами и значениями. Вообще говоря, функции могут быть не всюду определенными, так что говоря о функции n аргументов (функции из Nn в N, n -местной функции), мы имеем в виду функцию, определенную на некотором подмножестве Nn со значениями в N.
Пусть имеется k -местная функция f и k штук n -местных функций g1,...,gk. Тогда из них можно сформировать одну n -местную функцию
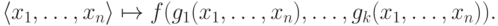
Говорят, что определенная таким образом функция получена из функций f и g1,...,gk с помощью операции подстановки.
Другая операция, называемая операцией рекурсии, или примитивной рекурсии, применяется к k -местной функции f и (k+2) -местной функции g. Ее результатом будет (k+1) -местная функция h, определяемая так:
h(x1,...,xk,0)=f(x1,...,xk); h(x1,...,xk,y+1)=g(x1,...,xk,y,h(x1,...,xk,y)).
В последовательности h(x1,...,xn,0),h(x1,...,xn,1),... каждое значение определяется через предыдущее, поэтому если какое-то из значений не определено, то не определены и все последующие.
Для единообразия будем считать, что нуль-местные функции (функции без аргументов) суть константы; это позволяет рекурсивно определять функции одной переменной.
Примитивно рекурсивными называют функции, которые можно получить с помощью операций подстановки и рекурсии из следующих базисных функций: константы 0, операции прибавления
единицы s : x 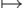 x+1 и семейства функций проекции:
это
семейство для каждого k
содержит k штук k -местных
функций
x+1 и семейства функций проекции:
это
семейство для каждого k
содержит k штук k -местных
функций 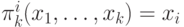 .
.
Функции проекции позволяют выполнять " неоднородные"
подстановки: скажем, можно получить функцию 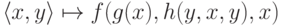 из функций f и h,
комбинируя их с
функциями проекции: сначала получаем функцию
из функций f и h,
комбинируя их с
функциями проекции: сначала получаем функцию 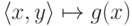 (подстановка
(подстановка 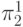 в g ),
затем
в g ),
затем 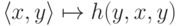 (подстановка
(подстановка 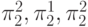 в h ), затем полученные две
функции
вместе с функцией
в h ), затем полученные две
функции
вместе с функцией 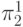 подставляем в f.
подставляем в f.
Подставляя константу 0 в функцию прибавления единицы, получаем константу (функцию нуля аргументов) 1. Затем можно получить константы 2, 3 и т.д.
Примеры примитивно рекурсивных функций
Как и с другими вычислительными моделями, важно накопить некоторый программистский опыт.
Сложение. Функция  получается с помощью рекурсии:
получается с помощью рекурсии:
sum(x,0)=x;
sum(x,y+1)=sum(x,y)+1.Надо, конечно, представить правую часть второго равенства как результат подстановки. Формально говоря, h(x,y,z) в определении рекурсии надо положить равным s(z), где s функция прибавления единицы.
Умножение. Функция  получается с помощью рекурсии
(с использованием сложения):
получается с помощью рекурсии
(с использованием сложения):
prod(x,0)=0;
prod(x,y+1)=prod(x,y)+x.Аналогичным образом можно перейти от умножения к возведению в степень.
Усеченное вычитание. Мы говорим об " усеченном вычитании"  при
при  и
и 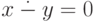 при
при  ,
поскольку мы имеем дело только с натуральными (целыми
неотрицательными) числами. Одноместная функция усеченного вычитания
единицы определяется рекурсивно:
,
поскольку мы имеем дело только с натуральными (целыми
неотрицательными) числами. Одноместная функция усеченного вычитания
единицы определяется рекурсивно:
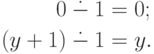
(Рекурсия здесь формальна, так как предыдущее значение не используется.) После этого усеченное вычитание для произвольных аргументов можно определить так: