Вычисления с оракулом
Машины с оракулом
Если множество B m -сводится к разрешимому множеству A, то и B разрешимо. Более того, если даже A и неразрешимо, но у нас есть доступ к "оракулу" для A, который отвечает на вопросы о принадлежности чисел множеству A, то мы можем с его помощью отвечать на вопросы о принадлежности чисел множеству B. В самом деле, если f сводящая функция и если мы хотим узнать, принадлежит ли некоторое число x множеству B, достаточно спросить у оракула, принадлежит ли f(x) множеству A.
Легко видеть, что m -сводимость использует возможности оракула довольно ограниченным образом: во-первых, оракулу задается только один вопрос, во-вторых, ответ на этот вопрос и считается ответом на исходный вопрос о принадлежности числа x множеству B. Вот пример, не укладывающийся в такую схему: имея оракул для множества A, мы можем отвечать на вопросы о принадлежности чисел множеству B=N \ A. Здесь вопрос по-прежнему один, но ответ на него заменяется на противоположный. Другой пример: имея оракул для множества A, можно отвечать на вопросы о принадлежности пары натуральных чисел множеству B=A x A. (Здесь оракулу надо задать уже два вопроса.)
Поэтому естественно желание отказаться от этих ограничений и дать общее определение сводимости множества B к множеству A. Наиболее общее и естественное определение таково: B сводится к A, если существует алгоритм, который разрешает множество B при условии, что ему предоставлен доступ к оракулу, отвечающему на вопросы про множество A. В более программистских терминах: есть алгоритм, содержащий вызовы внешней функции a(x:integer):boolean (не описанной внутри алгоритма); этот алгоритм разрешает множество B, если вызовы a(x) возвращают правильные ответы про множество A.
Этот вид сводимости называется сводимостью по Тьюрингу, или T -сводимостью. Обозначение: B <=T A означает, что B сводится по Тьюрингу к A. Вот несколько простых фактов про T -сводимость:
Теорема 43. (а) Если B <=m A, то B <=T A. (б) A <=T N \ A при любом A. (в) Если A <=T B и B <=T C, то A <=T C. (г) Если A <=T B и B разрешимо, то A разрешимо.
Все эти утверждения почти очевидны поясним, например, утверждение (в). Пусть у нас есть алгоритм для A, включающий вызовы внешней разрешающей процедуры для B, а также алгоритм для B, включающий вызовы внешней процедуры для C. Тогда можно заменить вызовы внешней B -процедуры на этот второй алгоритм и получится разрешающий алгоритм для A, использующий вызовы внешней процедуры для C.
Заметим, что (в отличие от m -сводимости) неперечислимое множество вполне может T -сводиться к перечислимому. Например, дополнение перечислимого неразрешимого множества K сводится к самому множеству K.
Можно говорить не только о сводимости к множеству A, но и вообще об алгоритмах, имеющих доступ к оракулу для множества A. Пусть такой алгоритм вычисляет некоторую функцию f. Это означает, напомним, что если f(x) определено, то на входе x алгоритм останавливается и дает ответ f(x), а если f(x) не определено, то не останавливается. (Предполагается, естественно, что оракул " не зависает" и выдает ответы, притом правильные, на все заданные ему вопросы.) В этом случае говорят, что (частичная) функция f вычислима относительно множества A.
В нашем определении сводимости вызываемая внешняя функция
принимала только два значения (" да" и " нет"). Такое
ограничение вовсе не обязательно. Пусть 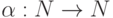 произвольная всюду
определенная функция. Тогда можно говорить о функциях, вычислимых относительно
произвольная всюду
определенная функция. Тогда можно говорить о функциях, вычислимых относительно  ;
вычисляющие их алгоритмы
включают в себя вызовы функции
;
вычисляющие их алгоритмы
включают в себя вызовы функции 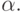 Однако это обобщение
не является существенным:
Однако это обобщение
не является существенным:
Теорема 44. Частичная функция f вычислима относительно всюду
определенной функции  тогда и только тогда, когда она вычислима относительно
множества, являющегося графиком функции
тогда и только тогда, когда она вычислима относительно
множества, являющегося графиком функции 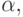 то есть
относительно множества
то есть
относительно множества 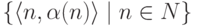 .
.
В самом деле, если мы можем вызывать функцию 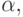 то можем
и отвечать на вопросы о принадлежности произвольной пары графику
функции
то можем
и отвечать на вопросы о принадлежности произвольной пары графику
функции 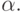 Напротив, если мы можем разрешать
график
Напротив, если мы можем разрешать
график 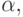 то можем найти
то можем найти 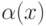 для
данного x,
задавая по очереди
вопросы о принадлежности графику пар
для
данного x,
задавая по очереди
вопросы о принадлежности графику пар 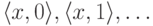 , пока не получим положительный ответ.
, пока не получим положительный ответ.
Определяя вычислимость относительно функции 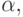 мы
предполагали,
что
мы
предполагали,
что  всюду определена. Это ограничение принципиально: для
не всюду определенных функций механизм обращения к ним (как к внешним
процедурам) требует уточнений. Допустим, мы вызвали
всюду определена. Это ограничение принципиально: для
не всюду определенных функций механизм обращения к ним (как к внешним
процедурам) требует уточнений. Допустим, мы вызвали 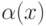 , а
оказалось,
что функция
, а
оказалось,
что функция  не определена на x. Означает ли
это, что алгоритм
" зависает" и уже не может выдать результат?
Или мы можем параллельно развернуть какие-то вычисления и
в каких-то случаях выдать результат, не дожидаясь ответа
от
не определена на x. Означает ли
это, что алгоритм
" зависает" и уже не может выдать результат?
Или мы можем параллельно развернуть какие-то вычисления и
в каких-то случаях выдать результат, не дожидаясь ответа
от 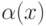 ?
Можем ли мы параллельно запросить несколько значений
функции
?
Можем ли мы параллельно запросить несколько значений
функции  Скажем, является ли функция f(x), заданная
формулой
Скажем, является ли функция f(x), заданная
формулой
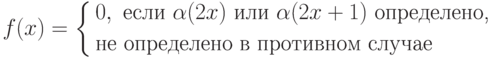
вычислимой относительно  Короче говоря, в отличие от
случая всюду определенных функций, тут есть разные (и притом не
эквивалентные) варианты определений, и всегда надо уточнять,
какое именно понятие имеется в виду. Поэтому мы, говоря о
вычислимости относительно некоторой функции
Короче говоря, в отличие от
случая всюду определенных функций, тут есть разные (и притом не
эквивалентные) варианты определений, и всегда надо уточнять,
какое именно понятие имеется в виду. Поэтому мы, говоря о
вычислимости относительно некоторой функции 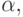 предполагаем, что функция
предполагаем, что функция  всюду определена.
всюду определена.
59. Пусть есть два различных множества X и Y. Будем рассматривать программы, имеющие доступ к двум оракулам для X и для Y, и функции, которые можно вычислить с помощью таких программ. Покажите, что это определение не дает ничего существенно нового, указав такое множество Z, что X - Y -вычислимость совпадает с Z -вычислимостью.
Эквивалентное описание
Сейчас мы дадим эквивалентное определение вычислимости функции
относительно 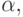 не апеллирующее к программам с вызовом
оракула.
не апеллирующее к программам с вызовом
оракула.
Мы называли образцом функцию с натуральными аргументами и
значениями, определенную на конечном подмножестве натурального
ряда. Такой образец задается списком
пар 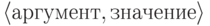 ;
образцы можно вычислимо пронумеровать, после чего
не различать образец и его номер и говорить о
разрешимом множестве образцов, перечислимом множестве образцов и т.д.
;
образцы можно вычислимо пронумеровать, после чего
не различать образец и его номер и говорить о
разрешимом множестве образцов, перечислимом множестве образцов и т.д.
Два образца называются совместными, если объединение их графиков есть по-прежнему график функции, то есть если нет такой точки, в которой оба они были бы определены и принимали разные значения.
Пусть имеется множество M троек вида 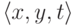 ,
где x и y натуральные числа, а t
образец. Будем
говорить, что две тройки
,
где x и y натуральные числа, а t
образец. Будем
говорить, что две тройки 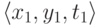 и
и 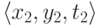 противоречат друг другу,
если x1=x2,
противоречат друг другу,
если x1=x2, 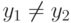 , а
образцы t1 и t2 совместны.
Множество M будем называть корректным, если в нем
нет противоречащих друг другу троек.
, а
образцы t1 и t2 совместны.
Множество M будем называть корректным, если в нем
нет противоречащих друг другу троек.
Пусть M корректное множество, а  некоторая
функция. Отберем в M все тройки вида
некоторая
функция. Отберем в M все тройки вида 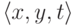 ,
для которых t является частью
,
для которых t является частью  (график t является
подмножеством графика
(график t является
подмножеством графика  ). Входящие в них образцы
совместны, поэтому (в силу корректности) среди отобранных троек
нет двух, у которых первые члены равны, а вторые нет.
Значит, отбросив третьи компоненты в отобранных тройках, мы
получим график некоторой функции (вообще говоря, частичной).
Будем обозначать эту функцию
). Входящие в них образцы
совместны, поэтому (в силу корректности) среди отобранных троек
нет двух, у которых первые члены равны, а вторые нет.
Значит, отбросив третьи компоненты в отобранных тройках, мы
получим график некоторой функции (вообще говоря, частичной).
Будем обозначать эту функцию ![M[\alpha ]](/sites/default/files/tex_cache/d9d17df891b6073e8ca38bb7c2d0982f.png) .
.
Теорема 45.
Частичная функция f : N -> N вычислима
относительно всюду определенной
функции 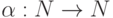 тогда и только тогда, когда
существует перечислимое корректное множество троек M, для
которого
тогда и только тогда, когда
существует перечислимое корректное множество троек M, для
которого ![f = M[\alpha ]](/sites/default/files/tex_cache/7b5b6e26298ba9692862aef499300cc2.png) .
.
Пусть имеется программа p, вычисляющая f и
включающая в себя
обращения к внешней процедуре 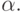 Будем для всех
натуральных n моделировать работу этой программы на
входе n по
всем путям, то есть предусматривая все возможные
значения
Будем для всех
натуральных n моделировать работу этой программы на
входе n по
всем путям, то есть предусматривая все возможные
значения 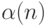 для каждого обращения к внешней процедуре. Для
каждого n получается дерево вариантов каждому обращению к
внешней процедуре соответствует развилка со счетным ветвлением.
На некоторых ветвях этого дерева вычисления завершаются и
программа выдает ответ. Как только мы обнаруживаем, что на
входе x возможен ответ y (на некоторой ветви), мы
образуем
тройку
для каждого обращения к внешней процедуре. Для
каждого n получается дерево вариантов каждому обращению к
внешней процедуре соответствует развилка со счетным ветвлением.
На некоторых ветвях этого дерева вычисления завершаются и
программа выдает ответ. Как только мы обнаруживаем, что на
входе x возможен ответ y (на некоторой ветви), мы
образуем
тройку 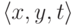 , где t образец,
содержащий все
аргументы и значения функции
, где t образец,
содержащий все
аргументы и значения функции 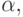 использованные на этой
ветви.
использованные на этой
ветви.
Полученное множество троек, которое мы обозначим M, будет
перечислимым (описанная процедура позволяет выписывать все его
элементы). В этом множестве нет противоречащих друг другу троек.
В самом деле,
если для одного и того же x в него вошли тройки  и
и  с
с 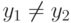 ,
то они соответствуют разным путям в дереве вычислений на одном
и том же входе x. Эти пути
в каком-то месте разошлись, то есть на один и тот же вопрос в
них были получены разные ответы. Эти ответы вошли в
образцы t1 и t2, и потому эти образцы несовместны.
Итак,
множество M корректно.
,
то они соответствуют разным путям в дереве вычислений на одном
и том же входе x. Эти пути
в каком-то месте разошлись, то есть на один и тот же вопрос в
них были получены разные ответы. Эти ответы вошли в
образцы t1 и t2, и потому эти образцы несовместны.
Итак,
множество M корректно.
Пусть  всюду определенная функция. Присоединим ее к
программе p. После этого программа p вычисляет
функцию f.
Покажем, что
всюду определенная функция. Присоединим ее к
программе p. После этого программа p вычисляет
функцию f.
Покажем, что ![f=M[\alpha ]](/sites/default/files/tex_cache/138b608aca72f057f9e8a5cd736f0a1e.png) . В самом деле,
пусть f(x)=y, то
есть работа программы p на входе x дала
ответ y. Эта
работа включала в себя несколько вызовов функции
. В самом деле,
пусть f(x)=y, то
есть работа программы p на входе x дала
ответ y. Эта
работа включала в себя несколько вызовов функции  и
соответствовала некоторой ветви рассмотренного выше дерева. Пусть t образец, содержащий все заданные при этом вопросы и
полученные на них ответы. Тогда t является
частью
и
соответствовала некоторой ветви рассмотренного выше дерева. Пусть t образец, содержащий все заданные при этом вопросы и
полученные на них ответы. Тогда t является
частью 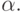 Кроме того, тройка
Кроме того, тройка 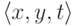 входит в
множество M.
Следовательно,
входит в
множество M.
Следовательно, ](/sites/default/files/tex_cache/c3619efd23bfe56b0aec1ddb48a67ac1.png) определено и равно y.
определено и равно y.
Напротив, если =y](/sites/default/files/tex_cache/231130c74ddb72d8a1b2a36916e68b80.png) , то существует
тройка
, то существует
тройка 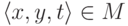 , для которой t является
частью
, для которой t является
частью 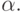 Эта тройка соответствует некоторой ветви
дерева вычислений. Поскольку t является
частью
Эта тройка соответствует некоторой ветви
дерева вычислений. Поскольку t является
частью 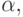 присоединение к программе p внешней процедуры
присоединение к программе p внешней процедуры  приведет к тому, что вычисления пойдут именно по этому
пути, и программа даст ответ y.
приведет к тому, что вычисления пойдут именно по этому
пути, и программа даст ответ y.
Итак, для любой программы p мы построили корректное множество M, которое задает ту же функцию, что и программа p, и первая половина утверждения теоремы доказана.
Чтобы доказать вторую половину, предположим, что имеется
корректное множество M, и построим эквивалентную ему
программу p. Эта программа будет (после присоединения к
ней оракула, вычисляющего  ) вычислять
функцию
) вычислять
функцию ![M[\alpha ]](/sites/default/files/tex_cache/d9d17df891b6073e8ca38bb7c2d0982f.png) . Программа p действует так:
получив вход x,
она перечисляет множество M и отбирает в нем тройки,
первым членом которых является x. Для каждой такой
тройки
. Программа p действует так:
получив вход x,
она перечисляет множество M и отбирает в нем тройки,
первым членом которых является x. Для каждой такой
тройки 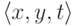 , вызывая внешнюю процедуру
(задавая вопросы оракулу) мы выясняем, является
ли t частью функции
, вызывая внешнюю процедуру
(задавая вопросы оракулу) мы выясняем, является
ли t частью функции 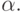 Если является, то
вычисление
заканчивается и выдается ответ y, если нет, перечисление
множества M продолжается.
Если является, то
вычисление
заканчивается и выдается ответ y, если нет, перечисление
множества M продолжается.
Очевидно, что построенная программа p вычисляет
функцию ![M[\alpha ]](/sites/default/files/tex_cache/d9d17df891b6073e8ca38bb7c2d0982f.png) .
.
60. Предположим, что мы провели это построение в обе стороны: сначала по корректному множеству M построили некоторую программу, как это описано во второй половине доказательства, а затем по программе построили некоторое корректное множество M'. Может ли M' отличаться от M?
