Вычисления с оракулом
0'-вычисления
В этом разделе мы рассмотрим вычислимость относительно m -полного перечислимого множества. Любые два таких множества m -сводятся друг к другу, и тем более T -сводятся друг к другу. Поэтому если какая-то функция вычислима относительно одного из них, то она вычислима и относительно другого. Такие функции называют 0' -вычислимыми.
Вспоминая, что множество пар  является одним из m -полных перечислимых множеств, можно сказать, что 0' -вычислимые функции вычисляются машинами, которым
придан специальный оракул, решающий проблему остановки: этому
оракулу посылают программу и вход, и он отвечает,
останавливается ли эта программа на этом входе или не
останавливается. (При этом посылаемая на экспертизу
программа самая
обычная, без обращений к оракулу.)
является одним из m -полных перечислимых множеств, можно сказать, что 0' -вычислимые функции вычисляются машинами, которым
придан специальный оракул, решающий проблему остановки: этому
оракулу посылают программу и вход, и он отвечает,
останавливается ли эта программа на этом входе или не
останавливается. (При этом посылаемая на экспертизу
программа самая
обычная, без обращений к оракулу.)
Ясно, что любое перечислимое множество является 0' -разрешимым, так как сводится к m -полному перечислимому множеству. (Обратное, очевидно, неверно дополнение к перечислимому неразрешимому множеству также 0' -разрешимо, но не перечислимо.)
Имеется следующее простое описание 0' -вычислимых функций:
Теорема 48. (а) Пусть T всюду определенная вычислимая функция двух натуральных аргументов. Перейдем к пределу по второму аргументу, рассмотрев функцию

(Эта функция уже не обязана быть всюду определенной, так как при некоторых x указанный предел может не существовать.) Функция t будет 0' -вычислимой. (б) Всякая 0' -вычислимая функция t может быть получена указанным образом из некоторой вычислимой всюду определенной функции T.
(a) Пусть T вычислимая всюду определенная функция двух
аргументов. Назовем пару 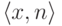 стабильной,
если T(x,n)=T(x,m) для данного x и для
всех m>n.
Заметим, что множество нестабильных пар перечислимо (найдя
две пары
стабильной,
если T(x,n)=T(x,m) для данного x и для
всех m>n.
Заметим, что множество нестабильных пар перечислимо (найдя
две пары 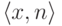 и
и 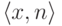 с n<m и
с n<m и 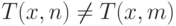 , мы включаем
пару
, мы включаем
пару 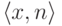 в перечисление всех нестабильных пар). Поэтому
множество нестабильных пар 0' -разрешимо. Другими словами, 0' -алгоритм для любой пары может проверить,
стабильна ли она.
в перечисление всех нестабильных пар). Поэтому
множество нестабильных пар 0' -разрешимо. Другими словами, 0' -алгоритм для любой пары может проверить,
стабильна ли она.
Рассмотрим теперь следующий 0' -алгоритм вычисления
предельной функции t. Получив вход x, мы
рассматриваем по
очереди пары 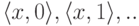 . и
для каждой из них проверяем, является ли она стабильной. Как
только стабильная пара
. и
для каждой из них проверяем, является ли она стабильной. Как
только стабильная пара 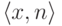 будет обнаружена,
значение T(x,n) выдается в качестве результата. Очевидно,
описанный 0' -алгоритм вычисляет
функцию t.
будет обнаружена,
значение T(x,n) выдается в качестве результата. Очевидно,
описанный 0' -алгоритм вычисляет
функцию t.
(б) Докажем теперь обратное утверждение. Пусть t частичная 0' -вычислимая функция одного аргумента. Нам надо построить вычислимую (в обычном смысле) всюду определенную функцию двух аргументов T, для которой

при всех x (и обе части этого равенства определены одновременно). Прежде всего мы сделаем себе небольшое послабление, разрешив функции T принимать также и некоторое специальное значение, которое мы будем обозначать звездочкой. При этом
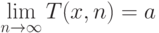
 ).
).Такое послабление на самом деле несущественно: если в последовательности, в которой есть звездочки, каждую из них заменить на два различных подряд идущих члена (все равно каких), то последовательность будет иметь прежний предел (или по-прежнему не иметь предела).
Теперь определим функцию T. По предположению
функция t
вычисляется некоторой программой p, имеющей доступ к
характеристической функции некоторого перечислимого множества K.
Обозначим через Kn конечное подмножество
множества K,
состоящее из тех его элементов, которые успели обнаружиться
за n шагов
перечисления множества K. Вычисляя T(x,n), мы
сделаем n шагов работы программы p, при этом
используя вместо K его конечное приближение Kn.
Если за
эти n шагов программа p не даст ответа (что может
быть по
разным причинам отведенное ей время может быть недостаточно, Kn может отличаться от K, да и вообще
функция t на x
может быть не определена), то 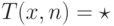 . Если же за n шагов
программа ответ даст, то этот ответ и будет значением T(x,n)
(за одним исключением, о котором мы скажем позже).
. Если же за n шагов
программа ответ даст, то этот ответ и будет значением T(x,n)
(за одним исключением, о котором мы скажем позже).
Попробуем доказать, что

Но нам надо еще доказать, что если предел существует и равен a, то t(x)=a. Здесь нас ожидает трудность, состоящая в следующем. Пусть при настоящем K работа программы p не завершается. Но тем не менее может получиться так, что при каждом n наше вычисление завершится за счет того, что множество Kn отличается от настоящего K, и даже случайно все эти вычисления дадут одинаковый ответ.
Чтобы справиться с этой трудностью, изменим определение
функции T.
А именно, договоримся, что если при вычислении T(x,n)
и T(x,n-1)
протоколы обращений к оракулу были разными (задавались
разные вопросы или были получены разные ответы на одинаковые
вопросы), то 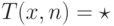 . Это не портит нашего предыдущего
рассуждения, поскольку там при больших n задаваемые вопросы и
даваемые ответы такие же, как в " настоящем" вычислении.
Зато теперь мы можем быть уверены, что если последовательность T(x,0),T(x,1),... имеет предел, то и t(x) определено. В
самом деле, если она имеет предел, то содержит конечное число
звездочек. Значит, при всех достаточно больших n оракулу
задаются одни и те же вопросы и получаются одни и те же ответы.
Значит, эти ответы правильны, так как в пределе Kn стремится
к K.
Поэтому настоящее вычисление также завершается (с тем
же ответом).
. Это не портит нашего предыдущего
рассуждения, поскольку там при больших n задаваемые вопросы и
даваемые ответы такие же, как в " настоящем" вычислении.
Зато теперь мы можем быть уверены, что если последовательность T(x,0),T(x,1),... имеет предел, то и t(x) определено. В
самом деле, если она имеет предел, то содержит конечное число
звездочек. Значит, при всех достаточно больших n оракулу
задаются одни и те же вопросы и получаются одни и те же ответы.
Значит, эти ответы правильны, так как в пределе Kn стремится
к K.
Поэтому настоящее вычисление также завершается (с тем
же ответом).
61. Приведенное в задаче 14 определение вычислимого действительного числа
можно релятивизовать относительного любого множества A. Покажите,
что число  является 0' -вычислимым
тогда и
только тогда, когда оно является пределом вычислимой
последовательности рациональных чисел.
является 0' -вычислимым
тогда и
только тогда, когда оно является пределом вычислимой
последовательности рациональных чисел.
Несравнимые множества
Определение сводимости по Тьюрингу (напомним, что A сводится по Тьюрингу к B, если множество A разрешимо с оракулом для B ) можно рассматривать как способ сравнивать задачи разрешения различных множеств " по трудности". (Если A <=T B, то задача разрешения множества A в некотором смысле проще, чем задача разрешения множества B.)
Возникает множество естественных вопросов, связанных с такой классификацией. Например, существует ли самая трудная в мире задача разрешения, то есть такое множество A, что B <=T A для любого множества B? Ответ, как легко понять, отрицательный: в релятивизованном относительно A мире есть свои неразрешимые множества (и даже A -перечислимые A -неразрешимые множества) поскольку там выполнены обычные теоремы теории алгоритмов. (Можно также заметить, что поскольку различных программ счетное число, то при любом множестве A семейство всех A -разрешимых множеств счетно.)
Другой, менее тривиальный вопрос такой: любые ли два множества сравнимы? Оказывается, что нет, как показывает следующая теорема, доказанная Клини и Постом.
Теорема 49.
Существуют два множества A и B, для
которых 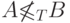 и
и  .
Эти множества можно взять 0' -разрешимыми.
.
Эти множества можно взять 0' -разрешимыми.
Множества A и B должны удовлетворять таким требованиям: никакая программа, к которой присоединен B -оракул, не разрешает множества A, и никакая программа, к которой присоединен A -оракул, не разрешает множества B.
Таким образом, имеется счетное число требований (поскольку есть счетное число программ). Мы будем обслуживать их по очереди, каждое по одному разу обеспечив выполнение некоторого требования, мы уже к нему возвращаться не будем. После каждого шага будет фиксировано поведение множеств A и B на некоторых отрезках натурального ряда, гарантирующее выполнение уже рассмотренных требований. На следующем шаги эти отрезки будут больше, и так далее в пределе получатся два множества A и B, удовлетворяющие всем требованиям. Вся конструкция будет 0' -вычислимой, так что результирующие множества будут 0' -разрешимыми.
