Свойства главных нумераций
Множества номеров
Начнем с такого примера. Рассмотрим множество номеров нигде не определенной функции для какой-либо главной нумерации. Будет ли оно разрешимо? Другими словами, можно ли по номеру функции в главной нумерации определить, является ли эта функция нигде не определенной?
Прежде чем отвечать на этот вопрос, заметим, что ответ не зависит от того, какая главная нумерация выбрана. В самом деле, если есть две разные главные нумерации, то они, как говорят, " сводятся " друг к другу: по номеру функции в одной нумерации можно алгоритмически получить номер той же функции в другой нумерации. Если бы в одной нумерации можно было бы проверять " нигде-не-определенность" функции, то это можно было бы делать и в другой (применив " функции перехода").
Следующая теорема показывает, что ответ на исходный вопрос будет отрицательным.
Теорема 20. Пусть U произвольная главная универсальная функция. Тогда множество тех n, при которых функция Un является нигде не определенной, неразрешимо.
Используем метод, называемый " сведением " покажем, что если бы это множество было разрешимым, то и вообще любое перечислимое множество было бы разрешимым. (Что, как мы знаем, неверно.)
Пусть K произвольное перечислимое неразрешимое множество. Рассмотрим такую вычислимую функцию V двух аргументов:

Как видно, второй аргумент этой функции фиктивен, и она по
существу совпадает с полухарактеристической функцией
множества K от первого аргумента. Очевидно, эта функция имеет
сечения
двух типов: при 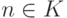 сечение Vn является
нулевой
функцией, при
сечение Vn является
нулевой
функцией, при 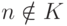 нигде не определенной функцией.
нигде не определенной функцией.
Так как функция U является главной, существует
вычислимая всюду определенная
функция s, для
которой V(n,x) = U(s(n),x) при всех n
и x, т.е. Vn = Us(n).
Поэтому при 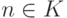 значение s(n) является U -номером нулевой функции, а при
значение s(n) является U -номером нулевой функции, а при 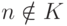 значение s(n)
является U -номером нигде не определенной функции. Поэтому если
бы
множество U -номеров нигде не определенной функции разрешалось бы
некоторым алгоритмом, то мы бы могли применить этот алгоритм
к s(n) и узнать, принадлежит ли число n
множеству K или нет.
Таким образом, множество K было бы разрешимым в противоречии с
нашим предположением.
значение s(n)
является U -номером нигде не определенной функции. Поэтому если
бы
множество U -номеров нигде не определенной функции разрешалось бы
некоторым алгоритмом, то мы бы могли применить этот алгоритм
к s(n) и узнать, принадлежит ли число n
множеству K или нет.
Таким образом, множество K было бы разрешимым в противоречии с
нашим предположением.
В частности, мы можем заключить, что нигде не определенная функция имеет бесконечно много номеров в любой главной нумерации (поскольку любое конечное множество разрешимо).
Кроме того, можно заметить, что множество номеров нигде не определенной функции не только не разрешимо, но и не перечислимо. В самом деле, его дополнение множество всех номеров всех функций с непустой областью определения перечислимо. (Это верно для любой вычислимой нумерации, а не только для главной: параллельно вычисляя U(n,x) для всех n и x, мы можем печатать те n, для которых обнаружилось x, при котором U(n,x) определено.) А если дополнение неразрешимого множества перечислимо, то само множество неперечислимо (по теореме Поста).
Справедливо и более общее утверждение, называемое иногда теоремой Успенского-Райса. Обозначим класс всех вычислимых функций (одного аргумента) через F.
Теорема 21. Пусть 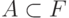 произвольное
нетривиальное свойство вычислимых функций (нетривиальность
означает, что есть как функции, ему удовлетворяющие, так и
функции, ему не удовлетворяющие, то есть что множество A непусто и не совпадает со всем F ). Пусть U главная универсальная функция. Тогда не существует алгоритма,
который по U -номеру вычислимой функции проверял бы, обладает
ли она свойством A. Другими словами, множество
произвольное
нетривиальное свойство вычислимых функций (нетривиальность
означает, что есть как функции, ему удовлетворяющие, так и
функции, ему не удовлетворяющие, то есть что множество A непусто и не совпадает со всем F ). Пусть U главная универсальная функция. Тогда не существует алгоритма,
который по U -номеру вычислимой функции проверял бы, обладает
ли она свойством A. Другими словами, множество 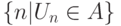 неразрешимо.
неразрешимо.
Посмотрим, принадлежит ли нигде не определенная функция
(обозначим ее  ) классу A, и возьмем
произвольную функцию
) классу A, и возьмем
произвольную функцию  " с другой стороны"
(если
" с другой стороны"
(если 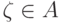 , то
, то 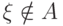 и
наоборот).
и
наоборот).
Далее действуем как раньше, но только вместо нулевой функции
возьмем функцию 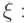 положим
положим

Как и раньше, функция V будет вычислимой (для
данных n и x
мы ожидаем появления n в множестве K, после
чего вычисляем 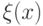 ). При
). При 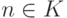 функция Vn
совпадает с
функция Vn
совпадает с 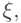 при
при 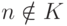 с
с 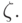 Таким
образом, проверяя свойство
Таким
образом, проверяя свойство 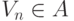 (если бы это можно
было сделать вопреки утверждению теоремы), можно было бы узнать,
принадлежит ли число n множеству K или нет.
(если бы это можно
было сделать вопреки утверждению теоремы), можно было бы узнать,
принадлежит ли число n множеству K или нет.
Некоторым недостатком этого доказательства является его
несимметричность (с одной стороны от A мы берем
нигде не определенную функцию, с другой стороны любую). Вот
более симметричный вариант. Покажем, что если
свойство A можно распознавать по U -номерам, то
любые два
непересекающихся
перечислимых множества P и Q отделимы
разрешимым множеством.
Выберем какие-нибудь две функции  и
и 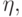 находящиеся
" по разные стороны" от A. Рассмотрим функцию
находящиеся
" по разные стороны" от A. Рассмотрим функцию

Эта функция вычислима: для заданных n и x ожидаем,
пока n появится либо в P, либо в Q,
после чего запускаем
вычисление соответственно 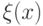 или
или 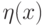 .
.
Если 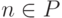 , то Vn совпадает
с
, то Vn совпадает
с  ; если
; если 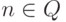 , то Vn совпадает с
, то Vn совпадает с 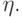 Поэтому, проверяя, принадлежит
ли Vn
классу A, мы могли бы разрешимо отделить P
от Q. Получаем противоречие, которое и завершает этот более
симметричный вариант доказательства.
Поэтому, проверяя, принадлежит
ли Vn
классу A, мы могли бы разрешимо отделить P
от Q. Получаем противоречие, которое и завершает этот более
симметричный вариант доказательства.
Второй вариант доказательства показывает, что верно следующее
усиление этой теоремы: для любых различных вычислимых
функций  и
и 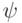 и любой главной универсальной
функции U
множества всех U -номеров функции
и любой главной универсальной
функции U
множества всех U -номеров функции  и
функции
и
функции 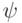 не
отделимы разрешимым множеством. (Заметим, что эти множества не
перечислимы, как мы впоследствии увидим.)
не
отделимы разрешимым множеством. (Заметим, что эти множества не
перечислимы, как мы впоследствии увидим.)
Теперь легко указать пример вычислимой универсальной функции, не являющейся главной. Достаточно сделать так, чтобы нигде не определенная функция имела единственный номер. Это несложно. Пусть U(n,x) произвольная вычислимая универсальная функция. Рассмотрим множество D всех U -номеров всех функций с непустой областью определения. Как мы уже говорили, это множество перечислимо. Рассмотрим всюду определенную вычислимую функцию d, его перечисляющую: D ={d(0),d(1),...}. Теперь рассмотрим функцию V(i,x), для которой V(0,x) не определено ни при каком x, а V(i+1,x) = U(d(i),x). Другими словами, функция V0 нигде не определена, а функция Vi+1 совпадает с Ud(i). Легко понять, что функция V вычислима; она универсальна по построению, и единственным V -номером нигде не определенной функции является число 0.
На самом деле существуют и более экзотические нумерации: как показал Фридберг, можно построить универсальную вычислимую функцию, для которой каждая вычислимая функция будет иметь ровно один номер. Соответствующие нумерации называют однозначными ; очевидно, они не могут быть главными. Забавная переформулировка: можно разработать такой язык программирования, в котором каждую программистскую задачу можно решить единственным образом. (Доказательство этой теоремы трудно и не приводится, на русском языке оно есть в книжке А.И.Мальцева " Алгоритмы и рекурсивные функции" [5]) вроде как на русском языке с других местах этого нет... Аналогичное утверждение верно и для нумераций перечислимых множеств.
