Теорема о неподвижной точке
Неподвижная точка и отношения эквивалентности
Теорема 25. Пусть U главная вычислимая универсальная функция для класса вычислимых функций одного аргумента, а h произвольная всюду определенная вычислимая функция одного аргумента. Тогда существует такое число n, что Un=Uh(n), то есть n и h(n) номера одной функции.
Другими словами, нельзя найти алгоритма, преобразующего программы, который бы по каждой программе давал другую (не эквивалентную ей). Эту теорему называют теоремой Клини о неподвижной точке или теоремой о рекурсии.
Мы будем действовать по аналогии с построением вычислимой функции, не имеющей всюду определенного вычислимого продолжения ( "лекция 2" ).
Рассмотрим произвольное отношение эквивалентности (которое мы
будем обозначать  ) на множестве натуральных чисел.
Мы покажем, что
следующие два свойства этого отношения не могут выполняться
одновременно:
) на множестве натуральных чисел.
Мы покажем, что
следующие два свойства этого отношения не могут выполняться
одновременно:
- Для всякой вычислимой функции f существует всюду определенная вычислимая функция g, являющаяся ее
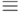 -продолжением (это означает, что если f(x) определено при некотором x, то
-продолжением (это означает, что если f(x) определено при некотором x, то  ).
). - Существует всюду определенная вычислимая функция h, не имеющая
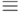 -неподвижной точки (то есть функция, для которой n
-неподвижной точки (то есть функция, для которой n 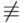 h(n) для всех n ).
h(n) для всех n ).
Если  отношение равенства ( x=y ),
то второе свойство
выполнено (положим, например, h(n)=n+1 ), поэтому не
выполнено первое.
Теорема о неподвижной точке получится, если
отношение равенства ( x=y ),
то второе свойство
выполнено (положим, например, h(n)=n+1 ), поэтому не
выполнено первое.
Теорема о неподвижной точке получится, если  понимать
как Ux=Uy ( x и y номера
одной и той же функции). В этом
случае выполнено первое свойство, как мы сейчас убедимся, и потому
не выполнено второе.
понимать
как Ux=Uy ( x и y номера
одной и той же функции). В этом
случае выполнено первое свойство, как мы сейчас убедимся, и потому
не выполнено второе.
Почему выполнено первое свойство? Пусть f произвольная
вычислимая функция одного аргумента. Рассмотрим
функцию V(n,x)=U(f(n),x).
Поскольку U является главной универсальной
функцией, найдется всюду определенная функция s, для
которой V(n,x)=U(s(n),x) при всех n
и x. Эта функция и будет
искомым 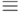 -продолжением. В самом деле, если f(n) определено, то s(n) будет другим номером той же
функции,
что и f(n).
(Отметим, что если f(n) не определено, то s(n) будет
одним
из номеров нигде не определенной функции.)
-продолжением. В самом деле, если f(n) определено, то s(n) будет другим номером той же
функции,
что и f(n).
(Отметим, что если f(n) не определено, то s(n) будет
одним
из номеров нигде не определенной функции.)
Для завершения доказательства теоремы о неподвижной точке осталось проверить, что указанные два свойства отношения эквивалентности несовместны. Это делается так же, как в теореме 10, где отношением эквивалентности было равенство. Возьмем вычислимую функцию f, от которой никакая вычислимая функция не может отличаться всюду (например, диагональную функцию x -> U(x,x) для некоторой вычислимой универсальной функции U ). По предположению существует всюду определенное вычислимое 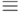 -продолжение g функции f. Рассмотрим функцию t(x)=h(g(x)), где h вычислимая всюду определенная функция, не имеющая
-продолжение g функции f. Рассмотрим функцию t(x)=h(g(x)), где h вычислимая всюду определенная функция, не имеющая 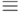 -неподвижной точки. Тогда t будет всюду отличаться от f. В самом деле, если f(x) определено, то
-неподвижной точки. Тогда t будет всюду отличаться от f. В самом деле, если f(x) определено, то 
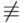 h(g(x))=t(x), и потому
h(g(x))=t(x), и потому 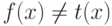 . Если же f(x) не определено, то этот факт сам по себе уже отличает f(x) и t(x).
. Если же f(x) не определено, то этот факт сам по себе уже отличает f(x) и t(x).
Теорему о неподвижной точке можно переформулировать и так:
Теорема 26. Пусть U(n,x) главная вычислимая универсальная функция для класса вычислимых функций одного аргумента. Пусть V(n,x) произвольная вычислимая функция. Тогда функции U и V совпадают на некотором сечении: найдется такое p, что Up=Vp, то есть U(p,n)=V(p,n) для любого n.
Так как функция U является главной, найдем такую всюду определенную вычислимую функцию h, что V(n,x)=U(h(n),x) при всех n и x. Осталось взять в качестве p неподвижную точку функции h.
(Пример следствия из этой теоремы: как бы ни старались разработчики, для любых двух версий компилятора существует программа, которая одинаково работает в обеих версиях например, зацикливается и там, и там. Впрочем, это все же не наверняка, а только если компилятор задает главную универсальную функцию но надо очень постараться, чтобы это было не так!)
Поучительно развернуть цепочку приведенных рассуждений и проследить, как строится неподвижная точка. Для наглядности вместо U(n,x) мы будем писать [n](x) и читать это " результат применения программы n к входу x ";
Рассуждение начинается с рассмотрения " диагональной " функции U(x,x), которую теперь можно записать
как [x](x)
(результат применения программы x к себе). Далее мы строим ее
всюду определенное 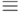 -продолжение. Это делается так.
Выражение [[x](x)](y) вычислимо зависит от двух аргументов. Мы
вспоминаем, что U есть главная универсальная функция, и
находим такую программу g, что [[g](x)](y)=[[x](x)](y) при
всех x и y. При этом [g](x) определено
для всех x. Пусть
мы хотим найти неподвижную точку программы h. Мы рассматриваем
композицию [h]([g](x)). Это выражение вычислимо зависит
от x,
и потому существует программа t, для
которой [t](x)=[h]([g](x)) при всех x. Эта
программа применима
ко всем x, поскольку таковы h и g.
Теперь неподвижной
точкой будет [g](t). Чтобы убедиться в этом, мы должны
проверить, что [[g](t)](x)=[[h]([g](t))](x) для
всех x. В
самом деле, по свойству g
имеем [[g](t)](x)=[[t](t)](x).
Вспоминая определение t, это выражение можно переписать как [[h]([g](t))](x) что как раз и требовалось.
-продолжение. Это делается так.
Выражение [[x](x)](y) вычислимо зависит от двух аргументов. Мы
вспоминаем, что U есть главная универсальная функция, и
находим такую программу g, что [[g](x)](y)=[[x](x)](y) при
всех x и y. При этом [g](x) определено
для всех x. Пусть
мы хотим найти неподвижную точку программы h. Мы рассматриваем
композицию [h]([g](x)). Это выражение вычислимо зависит
от x,
и потому существует программа t, для
которой [t](x)=[h]([g](x)) при всех x. Эта
программа применима
ко всем x, поскольку таковы h и g.
Теперь неподвижной
точкой будет [g](t). Чтобы убедиться в этом, мы должны
проверить, что [[g](t)](x)=[[h]([g](t))](x) для
всех x. В
самом деле, по свойству g
имеем [[g](t)](x)=[[t](t)](x).
Вспоминая определение t, это выражение можно переписать как [[h]([g](t))](x) что как раз и требовалось.
Программа, печатающая свой текст
Классическим примером применения теоремы о неподвижной точке является такое ее следствие: существует программа, печатающая (на любом входе) свой собственный текст. В самом деле, если бы такой программы не было, то преобразование
p 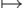 (программа, которая на любом входе печатает p )
(программа, которая на любом входе печатает p )
не имело бы неподвижной точки.
Формально говоря, это следствие можно выразить так:
Теорема 27. Пусть U(n,x) главная вычислимая универсальная функция для класса всех вычислимых функций одного аргумента. Тогда существует такое число p, что U(p,x)=p для любого x.
В программистских терминах: пусть U(p,x) результат применения паскаль-программы p к стандартному входу x. (Уточнения: (1) мы отождествляем числа и последовательности байтов; (2) если программа не завершает работы, мы считаем, что результат не определен, даже если на стандартный выход что-то послано.) Ясно, что функция U будет главной универсальной функцией. Поэтому к ней можно применить сформулированное только что утверждение; получим программу p, которая при любом входе на выходе дает p.
Ясно, что это рассуждение применимо для любого языка программирования; то, что мы упомянули язык паскаль, роли не играет.
34. Докажите, что существует паскаль-программа, которая печатает свой текст задом наперед.
35. Покажите, что есть две различные паскаль-программы P и Q с такими свойствами: программа P печатает текст программы Q, а программа Q печатает текст программы P. (Если не требовать различия между P и Q, то в качестве P и Q можно взять одну и ту же программу, печатающую свой текст.)
Выпишем явно программу на паскале, печатающую свой текст. (Это хорошая задача для любителей программирования.) Для начала напишем неформальную инструкцию на русском языке:
напечатать два раза, второй раз в кавычках, такой текст: "напечатать два раза, второй раз в кавычках, такой текст:"
Чтобы написать что-то похожее на паскале, понадобятся некоторые дополнительные хитрости, но идея ясна: строковая константа используется два раза. Вот один из возможных вариантов:
program selfprint; var a:array[1..100]of string;i:integer; begin a[1]:='program selfprint;'; a[2]:=' var a:array[1..100]of string;i:integer;'; a[3]:='begin'; a[4]:='for i:=1 to 3 do writeln(a[i]);'; a[5]:='for i:=1 to 11 do begin'; a[6]:=' write(chr(97),chr(91),i);'; a[7]:=' write(chr(93),chr(58),chr(61));'; a[8]:=' writeln(chr(39),a[i],chr(39),chr(59));'; a[9]:='end;'; a[10]:='for i:=4 to 11 do writeln(a[i]);'; a[11]:='end.'; for i:=1 to 3 do writeln(a[i]); for i:=1 to 11 do begin write(chr(97),chr(91),i); write(chr(93),chr(58),chr(61)); writeln(chr(39),a[i],chr(39),chr(59)); end; for i:=4 to 11 do writeln(a[i]); end.
Читая эту программу, полезно иметь в виду соответствие между символами и их кодами:
a [ ] : = ' ; 97 91 93 58 61 39 59
Видно, что эту программу легко модифицировать, чтобы она, скажем, печатала свой текст задом наперед вместо команд write и writeln, печатающих текст, надо написать команды, записывающие его в файл (или в массив байтов), а потом команды, печатающие этот файл или массив в обратном порядке.
Сделав еще один шаг, можно получить и доказательство теоремы о неподвижной точке. Пусть h некоторое преобразование паскаль-программ, у которого мы хотим найти неподвижную точку. Тогда напишем программу наподобие только что приведенной, которая будет записывать свой текст в строку p, затем применять h к p, получая некоторую другую строку q, а затем запускать интерпретатор Паскаля на строке q (используя в качестве входа программы q вход исходной программы). Конечно, эта программа уже не будет такой короткой, так как будет включать в себя (и даже два раза первый раз просто так, а второй раз в кавычках) интерпретатор паскаля, написанный на паскале.
Ясно, что такая программа будет неподвижной точкой преобразования h, так как ее выполнение начинается ровно с того, что вычисляется значение функции h на ее тексте, после чего это значение воспринимается как программа и применяется к входу.
На самом деле это доказательство в сущности повторяет предыдущее, только в более программистских терминах.
