Вычисления с оракулом
Релятивизация
Пусть фиксирована некоторая всюду определенная
функция 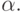 Тогда вся теория вычислимых функций может
быть, как говорят, " релятивизована" относительно
Тогда вся теория вычислимых функций может
быть, как говорят, " релятивизована" относительно 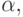 если во всех определениях и формулировках заменить вычислимые
функции на функции, вычислимые относительно
если во всех определениях и формулировках заменить вычислимые
функции на функции, вычислимые относительно  (которые для краткости называют также
(которые для краткости называют также  - вычислимыми ).
При этом все сформулированные выше результаты остаются
в силе, и доказательства остаются почти такими же.
- вычислимыми ).
При этом все сформулированные выше результаты остаются
в силе, и доказательства остаются почти такими же.
В частности, можно определить понятие перечислимого относительно  (или
(или  - перечислимого )
множества любым из эквивалентных способов: как область
определения
- перечислимого )
множества любым из эквивалентных способов: как область
определения  -вычислимой функции, как множество значений
-вычислимой функции, как множество значений  -вычислимой функции, как проекцию
-вычислимой функции, как проекцию  -разрешимого
(разрешимого относительно
-разрешимого
(разрешимого относительно  ) множества и т.д. Можно
указать и более прямое описание класса
) множества и т.д. Можно
указать и более прямое описание класса  -перечислимых
множеств.
-перечислимых
множеств.
Пусть E произвольноe множество пар вида 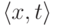 , где x число, а t образец. Пусть
, где x число, а t образец. Пусть  некоторая всюду определенная функция. Отберем в множестве E те
пары, у которых вторые члены являются частью
некоторая всюду определенная функция. Отберем в множестве E те
пары, у которых вторые члены являются частью  ; первые
члены таких пар образуют множество, которое мы
обозначим
; первые
члены таких пар образуют множество, которое мы
обозначим ![E[\alpha ]](/sites/default/files/tex_cache/52420a197b6443b0aadc5544cf5c55b9.png) .
.
Теорема 46.
Множество X является  -перечислимым тогда и
только
тогда, когда
-перечислимым тогда и
только
тогда, когда ![X=E[\alpha ]](/sites/default/files/tex_cache/e923b91a77db63d214fe16547cb1143b.png) для некоторого перечислимого
множества E. (Заметим, что в этом случае не требуется
никакого специального условия типа корректности.)
для некоторого перечислимого
множества E. (Заметим, что в этом случае не требуется
никакого специального условия типа корректности.)
Пусть X есть область определения вычислимой
относительно  функции f. Тогда
функции f. Тогда ![f=M[\alpha ]](/sites/default/files/tex_cache/138b608aca72f057f9e8a5cd736f0a1e.png) для некоторого
перечислимого корректного множества M. Оставим от всех троек
в M
только первый и третий члены; получится некоторое
перечислимое множество E. Легко проверить, что
для некоторого
перечислимого корректного множества M. Оставим от всех троек
в M
только первый и третий члены; получится некоторое
перечислимое множество E. Легко проверить, что ![E[\alpha ]](/sites/default/files/tex_cache/52420a197b6443b0aadc5544cf5c55b9.png) будет областью определения
функции
будет областью определения
функции ![M[\alpha ]=f](/sites/default/files/tex_cache/565383e469e38bedd431ec441b8d4b9d.png) , так
что
, так
что ![E[\alpha ]=X](/sites/default/files/tex_cache/469b716478e7823fedcffa8be9eb4763.png) .
.
Напротив, пусть ![X=E[\alpha ]](/sites/default/files/tex_cache/e923b91a77db63d214fe16547cb1143b.png) для
некоторого
для
некоторого 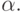 Тогда
рассмотрим множество M, которое получится, если в середину
каждой пары из E добавить число 0. Ясно, что
множество M
будет корректным и что
Тогда
рассмотрим множество M, которое получится, если в середину
каждой пары из E добавить число 0. Ясно, что
множество M
будет корректным и что ![M[\alpha ]](/sites/default/files/tex_cache/d9d17df891b6073e8ca38bb7c2d0982f.png) будет функцией, определенной
на
будет функцией, определенной
на ![X=E[\alpha ]](/sites/default/files/tex_cache/e923b91a77db63d214fe16547cb1143b.png) и принимающей только нулевые значения.
и принимающей только нулевые значения.
В обычной (нерелятивизованной) теории алгоритмов, важную роль играет теорема об универсальной функции. Она остается верной и после релятивизации:
Теорема 47.
Пусть  всюду определенная функция.
Существует вычислимая относительно
всюду определенная функция.
Существует вычислимая относительно  функция двух
аргументов, являющаяся универсальной для класса вычислимых
относительно
функция двух
аргументов, являющаяся универсальной для класса вычислимых
относительно  функций одного аргумента.
функций одного аргумента.
Как и в других случаях, можно почти без изменений воспроизвести
доказательство соответствующей нерелятивизованной теоремы.
Фиксируем какой-то язык программирования (предусматривающий
на этот раз вызовы внешних процедур) и перенумеруем все
программы, которые включают в себя вызовы внешней
процедуры 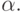 Теперь в качестве универсальной можно взять функцию
Теперь в качестве универсальной можно взять функцию

Мы использовали нижний индекс, чтобы подчеркнуть, что
функция 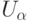 зависит от
зависит от 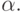 Впрочем, текст
вычисляющей
ее программы от
Впрочем, текст
вычисляющей
ее программы от  не зависит (хотя, естественно,
содержит вызовы функции
не зависит (хотя, естественно,
содержит вызовы функции  ).
).
Поучительно привести и другое доказательство, которое опирается на определение вычислимости в терминах корректных перечислимых множеств.
Рассмотрим универсальное перечислимое множество Z четверок
вида 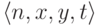 , где n, x
и y числа,
а t образец. Говоря об универсальности,
мы имеем в виду, что при различных n среди
сечений Zn
содержатся все перечислимые множества троек.
, где n, x
и y числа,
а t образец. Говоря об универсальности,
мы имеем в виду, что при различных n среди
сечений Zn
содержатся все перечислимые множества троек.
Среди этих перечислимых множеств троек могут быть и корректные, и некорректные. Мы хотим принудительно корректировать некорректные сечения, не меняя корректных. Другими словами, мы хотим построить новое перечислимое множество Z' с такими свойствами: во-первых, все сечения Z' корректны; во-вторых, если сечение Zn при некотором n было корректно, то оно не изменилось ( Z'n=Zn ).
Это делается просто: нужно перечислять Z, отбрасывая (не пропуская в Z' ) элементы, добавление которых делает некоторое сечение некорректным. Итак, мы построили перечислимое множество Z', универсальное для класса корректных перечислимых множеств.
Теперь легко указать корректное множество W, задающее
универсальную  -вычислимую функцию. Именно,
тройка
-вычислимую функцию. Именно,
тройка 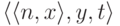 (теперь ее первым
членом является пара, так как универсальная функция зависит от
двух аргументов) принадлежит W, если
(теперь ее первым
членом является пара, так как универсальная функция зависит от
двух аргументов) принадлежит W, если 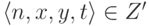 . Легко понять, что множество W
корректно.
При данной функции
. Легко понять, что множество W
корректно.
При данной функции  это
корректное множество задает некоторую
это
корректное множество задает некоторую  -вычислимую
функцию
-вычислимую
функцию 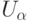 двух аргументов; ее n -ое сечение
есть
двух аргументов; ее n -ое сечение
есть ![Z'_{n}[\alpha ]](/sites/default/files/tex_cache/300509c5072a4a5afba01e45c4c12a9e.png) , где Z'n n -ое
сечение множества Z'.
Поэтому среди сечений функции
, где Z'n n -ое
сечение множества Z'.
Поэтому среди сечений функции 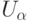 встречаются все
встречаются все  -вычислимые
функции, что и требовалось доказать.
-вычислимые
функции, что и требовалось доказать.
В релятивизованной теории алгоритмов имеется, конечно, и
аналог понятия главной универсальной функции:  -вычислимую функцию двух аргументов называют главной универсальной функцией для класса
-вычислимую функцию двух аргументов называют главной универсальной функцией для класса  -вычислимых функций одного аргумента,
если она
-вычислимых функций одного аргумента,
если она  -вычислима, универсальна для класса
-вычислима, универсальна для класса  -вычислимых функций одного аргумента и для
всякой
-вычислимых функций одного аргумента и для
всякой  -вычислимой функции V
двух аргументов существует всюду определенная
-вычислимой функции V
двух аргументов существует всюду определенная  -вычислимая функция s одного аргумента ("
транслятор"), для которой V(n,x)=U(s(n),x) при
всех n и x.
-вычислимая функция s одного аргумента ("
транслятор"), для которой V(n,x)=U(s(n),x) при
всех n и x.
Обычное доказательство (теорема 15) показывает,
что главные универсальные
функции для класса  -вычислимых функций существуют. Более
того, можно заметить, что построенная при доказательстве
(см. выше) функция s будет не только
-вычислимых функций существуют. Более
того, можно заметить, что построенная при доказательстве
(см. выше) функция s будет не только  -вычислимой, но и
просто вычислимой (в одном из вариантов доказательства функция s
имела
вид
-вычислимой, но и
просто вычислимой (в одном из вариантов доказательства функция s
имела
вид ![x\hm\mapsto[n,x]](/sites/default/files/tex_cache/7194c9397d606c67bb0ea71ababa70b8.png) , где квадратные скобки обозначают
фиксированную вычислимую нумерацию пар, а n некоторое
фиксированное число).
, где квадратные скобки обозначают
фиксированную вычислимую нумерацию пар, а n некоторое
фиксированное число).
Удобно, говоря о номерах  -вычислимых функций, иметь в
виду их номера в таких " сильно главных" нумерациях.
Естественная нумерация (порядковые номера программ)
является " сильно главной" нумерацией.
-вычислимых функций, иметь в
виду их номера в таких " сильно главных" нумерациях.
Естественная нумерация (порядковые номера программ)
является " сильно главной" нумерацией.
Говоря о релятивизованной теории алгоритмов, иногда употребляют такую метафору. Пусть A какое-то неразрешимое множество. Может оказаться, что есть такая внеземная цивилизация, которой множество A кажется разрешимым; глядя на число x, они сразу понимают, лежит ли оно в множестве A или нет, и эта проверка такое же элементарное действие в их программах, как у нас сравнение двух чисел. Тогда вся их теория алгоритмов будет автоматически релятивизованной относительно A, но они этого замечать не будут и потому прочтут наши рассуждения вплоть до этого раздела (не включая его) и согласятся со всеми теоремами. Более того, они могут прочесть и этот раздел о релятивизации но то, что для них будет B -вычислимым, для нас будет A - B -вычислимым (вычислимым с двумя оракулами A и B ).
Впрочем, к этой метафоре не стоит относиться слишком серьезно.
