|
Это в лекции 3. |
Хорновские формулы и задача получения продукции
Хорновские формулы
Определим вначале один интересный класс булевых формул - Хорновские формулы.
Определение 6.1. Пусть A - это множество логических (булевых) переменных. Хорновская (H-) формула - это формула вида
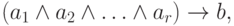
где 
Содержательно, такая Хорновская формула утверждает, что из истинности всех условий набора {a1, a2, ... , ar} следует истинность заключения b. Утверждения такого вида находят широкое применение в различных разделах информатики. В частности, в теории баз данных такой вид имеют "функциональные зависимости", в логическом программировании - правила логических программ, в автоматическом синтезе программ - "аксиомы вычислимости". В таком же виде формулируются правила вывода во многих экспертных системах.
В этих и других областях представляют интерес связанные между собой
задачи о минимальности набора H-формул и о выводимости некоторой H-формулы из заданного набора H -формул. Первая задача состоит в выяснении того, входит ли в набор H -формул F некоторая формула  которая может быть удалена из F без потери информации,
т.е. которая выводится из
которая может быть удалена из F без потери информации,
т.е. которая выводится из 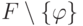 , а это и есть
задача о выводимости. Уточним эту задачу.
, а это и есть
задача о выводимости. Уточним эту задачу.
Определение 6.2. H-формула  является следствием или
выводится из множества H-формул F, если на всяком наборе
значений переменных из A, на котором истинны все формулы из F, истинна и
является следствием или
выводится из множества H-формул F, если на всяком наборе
значений переменных из A, на котором истинны все формулы из F, истинна и  (будем это обозначать как
(будем это обозначать как  ).
).
Это понятие следования некоторой формулы из множества формул можно сформулировать и для произвольных булевых формул, а не только для Хорновских. Следующее простое утверждение показывает, что понятие следования (выводимости) можно переформулировать в терминах тождественной истинности (см. определение 3.4).
Предложение 6.1. H-формула  является следствием множества H -формул F тогда и только тогда, когда формула
является следствием множества H -формул F тогда и только тогда, когда формула
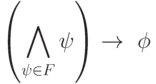 |
( *) |
является истинной на всех наборах значений переменных (т.е. тождественно истинной).
Доказательство непосредственно следует из определения значений конъюнкции и импликации.
Как уже отмечалось в п.3, проблема проверки по булевой формуле ее тождественной
истинности является весьма сложной. Известный нам метод такой проверки с помощью построения таблицы значений на всех наборах переменных практически не работает уже для формул с несколькими десятками переменных. В то же время во многих практических задачах число логических
параметров исчисляется сотнями. Оказывается, что для установления тождественной истинности формул вида (*) или, что то же самое, для задачи проверки условия  для H -формул имеется простой и очень эффективный алгоритм, позволяющий ее решать для формул с сотнями и тысячами переменных.
для H -формул имеется простой и очень эффективный алгоритм, позволяющий ее решать для формул с сотнями и тысячами переменных.
Мы изложим этот алгоритм на примере одного из интересных "экономических" приложений H-формул - задачи о возможности производства заданной продукции (набора товаров) из некоторого множества исходных продуктов (товаров, сырья).
Задача получения продукции
Пусть задано некоторое множество A={ a1, a2, ..., N} имен товаров (продуктов, сырья и т.п.) и имеется некоторое множество F технологических процессов (производств),
описывающих возможности получения одних продуктов из других. Каждый технологический процесс 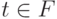 задается множеством
задается множеством 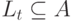 исходных продуктов (входов) этого процесса и результирующим продуктом (выходом)
исходных продуктов (входов) этого процесса и результирующим продуктом (выходом) 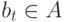 ,
т.е. процесс t позволяет из исходных продуктов Lt получить продукт bt - его выход.
Будем задавать технологический процесс в виде t: Lt -> bt.
Продукт, полученный в одном процессе, может далее использоваться в других процессах.
,
т.е. процесс t позволяет из исходных продуктов Lt получить продукт bt - его выход.
Будем задавать технологический процесс в виде t: Lt -> bt.
Продукт, полученный в одном процессе, может далее использоваться в других процессах.
Определение 6.3. Задача получения продукции
состоит в том, чтобы выяснить по заданному набору исходных продуктов 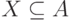 и результирующему продукту
и результирующему продукту 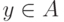 можно ли с помощью технологических процессов
из F получить выход y по входным продуктам из X .
можно ли с помощью технологических процессов
из F получить выход y по входным продуктам из X .
(Можно обобщить эту задачу и рассматривать возможность получения по X некоторого множества результирующих продуктов 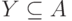 .)
.)
Пример 6.1. Пусть A= { дерево, клей, гвозди, кирпич, стекло, окна, полы, стены, крыша, столы}. Множество технологических процессов F={t1, t2, t3, t4, t5, t6} задается соответствующими множествами входов и выходов.
- t1: { дерево, клей, гвозди } -> столы
- t2: { дерево, гвозди} -> полы
- t3: { дерево, клей, стекло} -> окна
- t4: { стены, полы, крыша} -> дача
- t5: { кирпич, окна, дерево} -> стены
- t6: { дерево, гвозди } -> столы
Рассмотрим для этой системы технологических процессов задачу получения продукта дача по исходному множеству продуктов: {дерево, клей, гвозди, стекло, кирпич, крыша}.
Нетрудно понять, что эта задача решается положительно с помощью следующей цепочки процессов: t3; t5; t2; t4. Действительно, в t3 получаются окна, которые используются в t5 для получения стен, в t2 производятся полы, а затем произведенные ранее стены, полы, крыша используются в t4 для получения результата дача.
Подчеркнем, что мы абстрагируемся от количественных оценок исходных и производимых продуктов и считаем, что они всегда даются на входе и производятся в количестве, достаточном для обеспечения "сырьем" всех запускаемых процессов.
Построим формальную модель задачи о производстве с помощью булевых формул.
Будем рассматривать A как множество булевых переменных. Каждому процессу t с параметрами Lt={a1,... , ar} и bt сопоставим следующую H-формулу 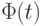 :
:
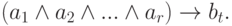
Например, процессу t5 из нашего примера соответствует формула  :
:
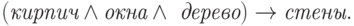
Сохраним для множества H -формул, соответствующих процессам, обозначение F.
Справедлива следующая теорема, которая показывает, что задача о возможности получения продукции и задача о следствии из множества H-формул эквивалентны.
Теорема 6.1. Для любых множества продуктов A, множества технологических процессов F, множества исходных продуктов 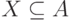 и результирующего продукта
и результирующего продукта 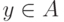 задача получения продукта y по входным продуктам из X с помощью процессов из F разрешима тогда и только тогда, когда
задача получения продукта y по входным продуктам из X с помощью процессов из F разрешима тогда и только тогда, когда 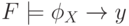 , где
, где 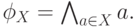
Доказательство  Предположим, что с помощью набора
процессов из множества F={t1, ..., th } из множества исходных продуктов X можно получить y.
Пусть
Предположим, что с помощью набора
процессов из множества F={t1, ..., th } из множества исходных продуктов X можно получить y.
Пусть 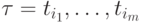 - это последовательность процессов из F,
которая приводит к получению y. Докажем, что тогда
- это последовательность процессов из F,
которая приводит к получению y. Докажем, что тогда 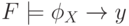 .
Рассмотрим произвольный набор значений переменных
.
Рассмотрим произвольный набор значений переменных 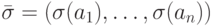 ,
на котором истинны все формулы из F. Если хотя бы для
одной переменной
,
на котором истинны все формулы из F. Если хотя бы для
одной переменной  ее значение
ее значение 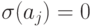 , то формула
, то формула 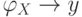 истинна, поскольку ее левая часть ложна. Предположим теперь, что для любой
переменной
истинна, поскольку ее левая часть ложна. Предположим теперь, что для любой
переменной  ее значение
ее значение 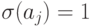 .
.
Тогда индукцией по номеру r процесса 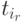 в
в  покажем, что для
каждого r=1, ..., m значение
соответствующей результирующей переменной
покажем, что для
каждого r=1, ..., m значение
соответствующей результирующей переменной 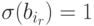 .
Действительно, при r=1 из применимости процесса
.
Действительно, при r=1 из применимости процесса 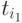 следует,
что
следует,
что 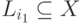 ,
но тогда
,
но тогда  для любой переменной
для любой переменной 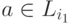 и левая часть
импликации
и левая часть
импликации 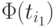 истинна на наборе
истинна на наборе  . Но так как и вся
формула
. Но так как и вся
формула 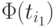 истинна на
истинна на  , то и
ее заключение
, то и
ее заключение 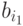 тоже истинно на
тоже истинно на  , т.е.
, т.е. 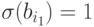 . Пусть теперь для некоторого k > 1\
. Пусть теперь для некоторого k > 1\ 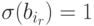 при r < k. Докажем, что и
при r < k. Докажем, что и 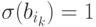 .
Поскольку процесс
.
Поскольку процесс 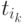 применим после процессов
применим после процессов 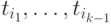 , то
, то 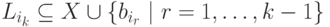 .
Тогда все переменные из
.
Тогда все переменные из 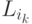 истинны на
истинны на  и, следовательно,
и, следовательно, 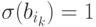 .
.
Из доказанного утверждения следует, что 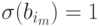 . Но
так как последовательность
. Но
так как последовательность  приводит к выпуску y, то
приводит к выпуску y, то  и, следовательно,
и, следовательно, 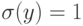 . Таким
образом, формула
. Таким
образом, формула 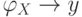 истинна на
истинна на  и
условие
и
условие 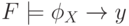 выполнено.
выполнено.
 Предположим теперь, что выполнено условие
Предположим теперь, что выполнено условие 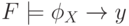 . Опишем построение последовательности процессов
. Опишем построение последовательности процессов 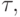 которая
приведет к производству y. Эта последовательность будет строиться по шагам.
На шаге i вместе с последовательностью
которая
приведет к производству y. Эта последовательность будет строиться по шагам.
На шаге i вместе с последовательностью 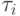 будем
Определять множество продуктов Xi, которые можно произвести, исходя из X с помощью
будем
Определять множество продуктов Xi, которые можно произвести, исходя из X с помощью 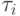 .
Процедура построения последовательности
.
Процедура построения последовательности 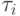 завершается, как только в нее включается некоторый процесс с результатом y,
либо когда на очередном этапе в Xi не добавляются новые элементы.
завершается, как только в нее включается некоторый процесс с результатом y,
либо когда на очередном этапе в Xi не добавляются новые элементы.
Шаг 0.Положим  , X0=X.
, X0=X.
Шаг 1. Положим 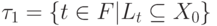 и
и  .
.
Пусть уже определены 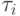 и Xi.
и Xi.
Шаг i+1. Положим 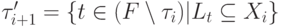 ,
,  и
и 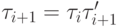 ( процессы внутри
( процессы внутри 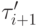 упорядочиваются
в произвольном порядке).
упорядочиваются
в произвольном порядке).
Если 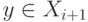 или Xi=Xi+1, то положим
или Xi=Xi+1, то положим 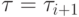 и закончим процедуру.
и закончим процедуру.
Заметим вначале, что эта процедура построения  обязательно завершится через конечное число шагов, так как размер Xi не может превысить размер множества всех продуктов A.
Покажем, что процесс построения
обязательно завершится через конечное число шагов, так как размер Xi не может превысить размер множества всех продуктов A.
Покажем, что процесс построения  завершится на таком шаге (i+1), для которого
впервые
завершится на таком шаге (i+1), для которого
впервые 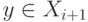 , т.е. что последовательность
процессов
, т.е. что последовательность
процессов  приводит к производству y.
Действительно, предположим, что процедура завершилась
после этапа (i+1) из-за выполнения равенства Xi=Xi+1 (при этом
приводит к производству y.
Действительно, предположим, что процедура завершилась
после этапа (i+1) из-за выполнения равенства Xi=Xi+1 (при этом 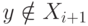 .
Покажем, что тогда существует
набор значений переменных
.
Покажем, что тогда существует
набор значений переменных 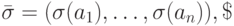 на
котором все формулы из F истинны, а формула
на
котором все формулы из F истинны, а формула 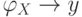 ложна.
Положим
ложна.
Положим  при
при 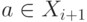 и
и  при
при 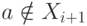 .
Так как
.
Так как 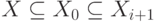 , то
для каждого
, то
для каждого 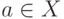 значение
значение  , а так
как
, а так
как 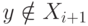 , то
, то 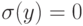 ,
т.е. формула
,
т.е. формула 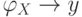 на наборе
на наборе  ложна. Каждая формула
ложна. Каждая формула 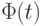 \ для
\ для 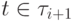 истинна, поскольку
истинна, поскольку 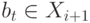 и, следовательно,
и, следовательно,  .
Ложной могла бы оказаться лишь такая формула
.
Ложной могла бы оказаться лишь такая формула 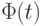 , для такого
процесса
, для такого
процесса 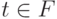 , у которого
заключение
, у которого
заключение 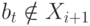 . Но для такого процесса t обязательно имеется
продукт
. Но для такого процесса t обязательно имеется
продукт 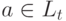 , который не входит в Xi (иначе
бы bt попало в Xi+1
и процедура не остановилась бы на (i+1) -ом шаге). Для этого a значение
, который не входит в Xi (иначе
бы bt попало в Xi+1
и процедура не остановилась бы на (i+1) -ом шаге). Для этого a значение  . Но тогда условие импликации
. Но тогда условие импликации 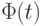 ложно на
ложно на  , а вся формула
, а вся формула 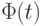 на нем истинна. Таким образом, мы пришли к противоречию, которое показывает, что
на нем истинна. Таким образом, мы пришли к противоречию, которое показывает, что 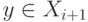 и процесс
и процесс  приводит к производству y.
приводит к производству y.
