|
Это в лекции 3. |
Хорновские формулы и задача получения продукции
Решение задачи о продукции
Можно ли построить эффективную процедуру, проверяющую разрешимость задачи о продукции или (что то же самое) задачи о следствии для H -формул? Процедура, описанная во второй части доказательства теоремы 6.1, является основой для следующего алгоритма, который строит множество всех продуктов, которые можно получить из исходных продуктов с помощью заданной системы технологических процессов.
Определение 6.4. Пусть F - множество технологических процессов, X - исходное множество продуктов. Замыкание X с помощью F - это множество продуктов
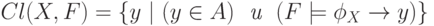
Приводимый ниже алгоритм ПрямаяВолна решает задачу о продукции в два этапа: на первом строится замыкание Cl(X,F), а на втором - проверяется, входит ли y в это замыкание. Итак, основную роль играет алгоритм построения замыкания ЗАМЫКАНИЕ (X,F). В нем переменные СТАРЫЕ и НОВЫЕ - это множества продуктов (истинных булевых переменных). Идея построения замыкания проста: вначале исходные данные из X заносятся в НОВЫЕ. Затем работа идет поэтапно. Перед началом каждого этапа полученные ранее НОВЫЕ передаются в СТАРЫЕ. После этого результаты всех технологических процессов, входы которых уже получены, т.е. содержатся в множестве НОВЫЕ, добавляются к этому множеству. Алгоритм завершает работу, когда на очередном этапе ничего не добавилось, т.е. нет технологических процессов, применение которых может расширить множество полученных продуктов.
Алгоритмы такого вида часто называются алгоритмами прямого поиска или поиска от данных.
Алгоритм ЗАМЫКАНИЕ(X,F)
Вход: множество технологических процессов F и множество исходных продуктов X.
Выход: множество продуктов НОВЫЕ (=Cl(X,F)).
1. СТАРЫЕ := ПУСТО; НОВЫЕ := X;
2. ПОКА НОВЫЕ != СТАРЫЕ ВЫПОЛНЯТЬ
3. { СТАРЫЕ := НОВЫЕ;
4. ДЛЯ КАЖДОГО процесса t принадлежит F ВЫПОЛНЯТЬ
5. ЕСЛИ {Lt} подмножество НОВЫЕ ТО НОВЫЕ := НОВЫЕ ОБЪЕДИНИТЬ {bt};
6. };
7. вернуть (НОВЫЕ).Алгоритм ПрямаяВолна(X,y,F)
1. Z := ЗАМЫКАНИЕ (X,F);
2. ЕСЛИ y принадлежит Z\ ТО вернуть ("ДА") ИНАЧЕ вернуть ("НЕТ").Следующая теорема утверждает корректность приведенного алгоритма.
Теорема 6.2.
Алгоритм ЗАМЫКАНИЕ(X,F) возвращает множество Cl(X,F),
а алгоритм ПрямаяВолна(X,y,F) выдает ответ "ДА" тогда и только тогда,
когда 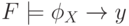 .
.
Доказательство этого утверждения фактически содержится в комментариях перед алгоритмом и его уточнение предоставляется читателю (см. задачу 6.2).
Пример 6.2. Рассмотрим работу алгоритма ЗАМЫКАНИЕ(X,F) на задаче получения y = дача по исходному множеству X = {дерево, клей, гвозди, стекло, кирпич, крыша} из примера 6.1.
В следующей таблице показаны шаги алгоритма, на которых изменяются значения переменных СТАРЫЕ и НОВЫЕ. В первом столбце этой таблицы указан номер соответствующей строки алгоритма, после строки 5 в скобках указан тот процесс, который приводит к увеличению множества НОВЫЕ.
| Стр. | СТАРЫЕ | НОВЫЕ |
|---|---|---|
| 1 |  |
дерево, клей, гвозди, кирпич, крыша, стекло |
| 3 | дерево, клей, гвозди, кирпич, крыша, стекло | дерево, клей, гвозди, кирпич, крыша, стекло |
| 5 (t1) | - " - | дерево, клей, гвозди, кирпич, крыша, стекло, столы |
| 5 (t2) | - " - | дерево, клей, гвозди, кирпич, крыша, стекло, столы, полы |
| 5 (t3) | - " - | дерево, клей, гвозди, кирпич, крыша, стекло, столы, полы, окна |
| 5 (t5) | - " - | дерево, клей, гвозди, кирпич, крыша, стекло, столы, полы, окна , стены |
| 3 | дерево, клей, гвозди, кирпич, крыша, стекло, столы, полы, окна, стены | дерево, клей, гвозди, кирпич, крыша, стекло, столы, полы, окна, стены |
| 5 (t4) | - " - | дерево, клей, гвозди, кирпич, крыша,стекло, столы, полы, окна , стены, дача |
| 3 | дерево, клей, гвозди, кирпич, крыша, стекло, столы, полы, окна, стены, дача | дерево, клей, гвозди, кирпич, крыша, стекло, столы, полы, окна, стены, дача |
Таким образом, в данном примере построение результирующего множества НОВЫЕ, равного Cl(X,F), завершается за два этапа, а на третьем выясняется, что ничего нового в него не может быть добавлено. После этого алгоритм ПрямаяВолна(X,y,F) проверит, что дача входит в Cl(X,F), и выдаст ответ "ДА".
С точки зрения сложности вычислений недостатком алгоритма ЗАМЫКАНИЕ(X,F) является то, что на каждой итерации основного цикла в строках 2-6 в строке 4 перебираются все процессы, даже уже отработавшие, а в строке 5 на вхождение в НОВЫЕ проверяются все элементы Lt даже те, вхождение которых в НОВЫЕ уже было установлено на предыдущих итерациях. Ниже приведен более эффективный алгоритм для построения замыкания1Этот алгоритм был независимо открыт несколькими авторами, рассматривающими различные эквивалентные формулировки в различных областях: в синтезе программ - А. Диковским (1979), в базах данных - К.Бирном и П. Бернстайном (1979), в логическом программировании - В.Доулингом и Дж. Гальером (1984). Мы, в основном, следуем изложению этого алгоритма в [11] .
На этапе инициализации в нем для каждого процесса t подсчитывается
число элементов в Lt и помещается в ячейку массива СЧЕТ [t], кроме того, для
каждого 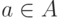 создается список СПИСОК [a] (номеров)
процессов,
во входы (левые части) которых входит продукт a. Далее в основной
части алгоритма
для каждого продукта a из множества НОВЫЕ, куда вначале
помещается X,
и каждого процесса t, в условие которого входит a,
из СЧЕТ [t]
вычитается 1. Если СЧЕТ [t] становится равным 0, это означает, что
все продукты из Lt уже получены и тогда его результат bt добавляется
в НОВЫЕ, если его там ранее не было. Для поиска таких t
используется СПИСОК [a].
Во множестве ОБНОВА хранятся уже полученные продукты из НОВЫЕ, которые еще не использовались для запуска новых процессов. Множества продуктов НОВЫЕ и ОБНОВА реализуются булевскими массивами длины |A|, единицы которых объединены в списки.
создается список СПИСОК [a] (номеров)
процессов,
во входы (левые части) которых входит продукт a. Далее в основной
части алгоритма
для каждого продукта a из множества НОВЫЕ, куда вначале
помещается X,
и каждого процесса t, в условие которого входит a,
из СЧЕТ [t]
вычитается 1. Если СЧЕТ [t] становится равным 0, это означает, что
все продукты из Lt уже получены и тогда его результат bt добавляется
в НОВЫЕ, если его там ранее не было. Для поиска таких t
используется СПИСОК [a].
Во множестве ОБНОВА хранятся уже полученные продукты из НОВЫЕ, которые еще не использовались для запуска новых процессов. Множества продуктов НОВЫЕ и ОБНОВА реализуются булевскими массивами длины |A|, единицы которых объединены в списки.
