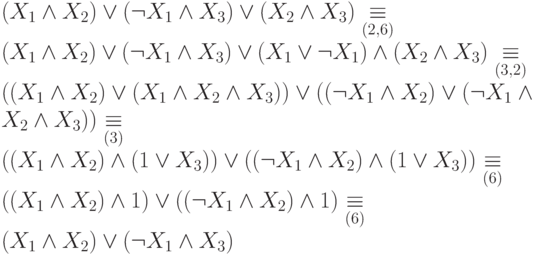|
Это в лекции 3. |
Эквивалентность формул и нормальные формы
Эквивалентность булевых формул
Определение 4.1. Булевы формулы  и
и  называются эквивалентными,
если соответствующие им функции
называются эквивалентными,
если соответствующие им функции 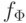 и
и 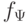 равны.
равны.
Обозначение:  . Эквивалентные формулы называют
также тождественно равными, а выражения вида
. Эквивалентные формулы называют
также тождественно равными, а выражения вида  логическими
тождествами
.
логическими
тождествами
.
Основные эквивалентности (тождества)
Таким образом, эквивалентные формулы являются различными заданиями одной и той же булевой функции. Ниже мы приводим ряд пар эквивалентных формул (тождеств), отражающих существенные свойства логических операций и важные соотношения между различными операциями. Они часто позволяют находить для булевых функций по одним задающим их формулам более простые формулы. Большинство из приводимых тождеств имеют собственные имена. Часто их называют законами логики.
Пусть  - это одна из функций
- это одна из функций 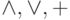 .
Для этих трех функций выполнены следующие две эквивалентности
( законы ассоциативности и коммутативности ).
.
Для этих трех функций выполнены следующие две эквивалентности
( законы ассоциативности и коммутативности ).
-
Ассоциативность:

( 1) -
Коммутативность:

( 2) -
Дистрибутивные законы:
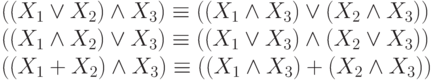
( 3) -
Двойное отрицание:
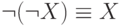
( 4) -
Законы де Моргана (внесение отрицания внутрь скобок):

( 5) -
Законы упрощения:
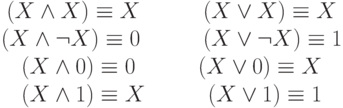
( 6)
Некоторые законы упрощения имеют собственные названия: эквивалентности в первой строке
называются законами идемпотентности, 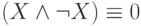 - это закон противоречия,
- это закон противоречия, 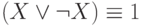 - это закон исключенного третьего. Эквивалентности в двух последних строках иногда называют законами 0 и 1.
- это закон исключенного третьего. Эквивалентности в двух последних строках иногда называют законами 0 и 1.
Следующие две эквивалентности позволяют выразить импликацию и сложение по модулю 2 через дизъюнкцию, конъюнкцию и отрицание.
 |
( 7) |
 |
( 8) |
Проверку правильности этих эквивалентностей оставляем читателям (см. задачу 4.1).
Эквивалентные преобразования формул
Соглашения об упрощенной записи формул.
-
Законы ассоциативности показывают, что значения формул,
составленных из переменных и одних операций конъюнкции, не зависят
от расстановки скобок. Поэтому вместо формул
 и
и 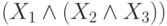 мы будем для упрощения писать
выражение
мы будем для упрощения писать
выражение 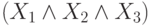 , которое не является формулой, но
может быть превращено в нее с помощью расстановки скобок. Аналогично, будем
использовать выражения
, которое не является формулой, но
может быть превращено в нее с помощью расстановки скобок. Аналогично, будем
использовать выражения  и (X1 + X2 + X3)
для сокращения формул, состоящих из одних дизъюнкций или одних сложений по модулю 2, соответственно.
и (X1 + X2 + X3)
для сокращения формул, состоящих из одних дизъюнкций или одних сложений по модулю 2, соответственно. - Если внешней функцией в формуле является одна из функций
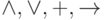 , то внешние скобки в записи формулы можно опустить.
, то внешние скобки в записи формулы можно опустить.
Таким образом, с использованием этих соглашений формула
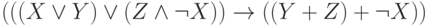
может быть записана как
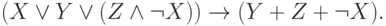
Из определения эквивалентности формул непосредственно следует Принцип замены эквивалентных подформул:
пусть формула  является подформулой формулы
является подформулой формулы  формула
формула 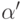 эквивалентна
эквивалентна  и формула
и формула  получена из
получена из  посредством замены некоторого вхождения
посредством замены некоторого вхождения  на
на 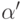 . Тогда
. Тогда  эквивалентна
эквивалентна  т.е.
т.е.  .
.
Применяя этот принцип и используя основные тождества, можно находить для
заданной формулы другие эквивалентные ей формулы. Часто это может приводить к
существенному упрощению исходной формулы.
Например, если в формуле  заменим на
основании тождеств (6) подформулу
заменим на
основании тождеств (6) подформулу 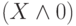 на 0, то получим эквивалентную формулу
на 0, то получим эквивалентную формулу 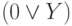 .
По закону коммутативности (2) эта формула эквивалентна
формуле
.
По закону коммутативности (2) эта формула эквивалентна
формуле 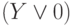 , которая, в свою очередь, по одному из тождеств группы
(6) эквивалентна формуле Y. Эту цепочку эквивалентных
преобразований можно записать также следующим образом:
, которая, в свою очередь, по одному из тождеств группы
(6) эквивалентна формуле Y. Эту цепочку эквивалентных
преобразований можно записать также следующим образом:

В этой цепочке вспомогательные номера под знаками эквивалентности указывают, с помощью какой группы основных тождеств эта эквивалентность получается.
Выведем еще несколько важных логических тождеств, позволяющих проводить упрощения сложных формул. Их называют законами поглощения.
-
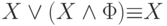
( П1) Действительно,
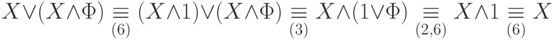
-
Действительно,

( П2) 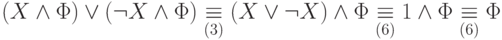
-
Действительно,
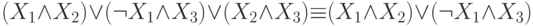
( П3)