|
Это в лекции 3. |
Полные системы функций и теорема Поста
Замкнутые классы функций
Пусть  - это множество всех
булевых функций. В предыдущем разделе мы установили, что любую функцию из
- это множество всех
булевых функций. В предыдущем разделе мы установили, что любую функцию из 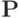 можно задать формулой над системой
можно задать формулой над системой 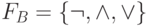 (в качестве таких формул можно,
например, взять соответствующие ДНФ и КНФ). Такие системы функций называются полными.
(в качестве таких формул можно,
например, взять соответствующие ДНФ и КНФ). Такие системы функций называются полными.
Определение 5.1. Система булевых функций F
называется полной,если формулами над этой системой можно задать
любую булеву функцию из 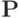 .
.
Другим уже известным нам примером полной системы функций является система FJ={ 0, 1, *, +}, позволяющая задать произвольную булеву
функцию с помощью многочлена Жегалкина. Разумеется, не всякая система является
полной. Например, формулами над системой 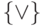 невозможно
выразить функцию тождественно равную 0 (почему?).Наша цель в этом разделе - найти критерий, позволяющий
по системе функций
определять ее полноту.
невозможно
выразить функцию тождественно равную 0 (почему?).Наша цель в этом разделе - найти критерий, позволяющий
по системе функций
определять ее полноту.
Для исследования полноты полезно следующее понятие.
Определение 5.2. Замыкание [F] системы функций F - это множество всех функций, которые можно задать с помощью формул над F .
Тогда определение полной системы можно переформулировать так:
система F является полной тогда и только тогда, когда ![[F] = \mathbf{P}](/sites/default/files/tex_cache/5d930636e9f73808ab8050fd241dd05c.png) .
.
Замыкание обладает следующими основными свойствами.
Предложение 5.1.
Доказательство. Все эти утверждения достаточно просто следуют из определения замыкания. Например, справедливость пункта (2) следует из того, что всякая функция из [F] задается некоторой формулой над F, а тогда всякая функция из [[F]], которая задается суперпозицией функций из [F], задается также некоторой формулой над F. Пункт (3) очевиден, а пункт (4) следует из (2) и (3):
![F \subseteq [G] \Rightarrow [F] \subseteq [[G]] \Rightarrow [F] \subseteq [G]](/sites/default/files/tex_cache/ef2b47c4de2cc866969d153d721963f3.png) и так как
и так как ![[F] = \mathbf{P}](/sites/default/files/tex_cache/5d930636e9f73808ab8050fd241dd05c.png) ,
то и
,
то и ![[G] = \mathbf{P}](/sites/default/files/tex_cache/74dfea5e9d68c4291b7a5d4145a9db9b.png) .
.
Утверждение (4) позволяет устанавливать полноту некоторой системы, выражая с ее помощью все функции другой системы, полнота которой уже установлена.
Например, законы де Моргана позволяют выразить 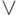 через пару
через пару 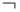 ,
, 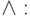
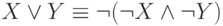 и
и 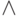 - через пару
- через пару 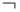 ,
, 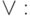
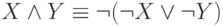 . Поэтому каждая из систем
. Поэтому каждая из систем 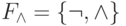 и
и 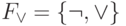 также является полной. Эквивалентности (7) и (8) позволяют выразить
также является полной. Эквивалентности (7) и (8) позволяют выразить 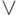 через пару
через пару 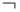 ,
, 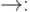
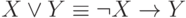 .
Следовательно, полной будет и система
.
Следовательно, полной будет и система 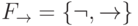 .
.
Имеются ли полные системы из одной двуместной функции? Да. Рассмотрим
систему, { | }, включающую лишь штрих Шеффера. Напомним, что 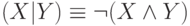 . Тогда нетрудно проверить, что
. Тогда нетрудно проверить, что 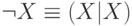 и
и 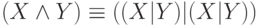 . Следовательно, система { | } полная.
. Следовательно, система { | } полная.
Определение 5.3. Система функций F называется замкнутой, если F = [F] .
Очевидно, что замкнутая система F, не содержащая всех функций
из 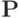 , не является полной.
, не является полной.
Далее в этом разделе мы будем использовать верхний индекс в круглых скобках
Для указания числа аргументов функции, т.е. f(n) означает, что 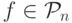 .
.
Определим пять важных замкнутых систем.
Определение 5.4.
(1,2) Функция 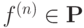 сохраняет 0 (сохраняет 1),если f(0,0,...
,0)=0 ( f(1,1,...,1) = 1 ). Класс всех функций, сохраняющих 0, обозначим через
сохраняет 0 (сохраняет 1),если f(0,0,...
,0)=0 ( f(1,1,...,1) = 1 ). Класс всех функций, сохраняющих 0, обозначим через 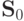 ,
а класс всех функций, сохраняющих 1, - через
,
а класс всех функций, сохраняющих 1, - через 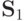 .
.
(3) Функция 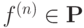 называется самодвойственной, если для любого набора аргументов
называется самодвойственной, если для любого набора аргументов 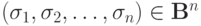 имеет место равенство:
имеет место равенство:

Таким образом, самодвойственные функции принимают на противоположных наборах
противоположные значения. Класс всех самодвойственных функций обозначим через 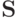 .
.
(4) Функция 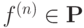 называется линейной, если она может
быть задана линейным многочленом Жегалкина вида
называется линейной, если она может
быть задана линейным многочленом Жегалкина вида
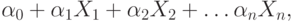
где 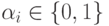 при i=0, 1, 2, ..., n.
при i=0, 1, 2, ..., n.
Класс всех линейных функций обозначим через 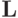 .
.
(5) Функция 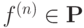 называется монотонной, если для любых
двух наборов аргументов
называется монотонной, если для любых
двух наборов аргументов 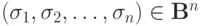 и
и 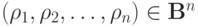 таких, что для всех
таких, что для всех ![j \in [1,n]](/sites/default/files/tex_cache/43744c20e46fb701151e3826dc547bc7.png)
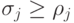 , имеет место неравенство
, имеет место неравенство
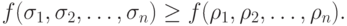
Класс всех монотонных функций обозначим через  .
.
Пример 5. Рассмотрим для примера пять функций от 3-х переменных, которые представлены в следующей таблице.
| X1 | X2 | X3 | f1 | f2 | f3 | f4 | f5 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1. | 1 | 0 | 1 | 1 | 1 | 1 |
Из определений непосредственно следует, что f3, f4 и f5
сохраняют 0, т.е. входят в 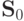 , а функции f2, f3, f4
и f5 сохраняют 1, т.е. входят в
, а функции f2, f3, f4
и f5 сохраняют 1, т.е. входят в 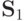 . Функция f3 является самодвойственной, а f2 - нет, так как f2(0,0,0) = f2(1,1,1). Функция f2 является линейной - она задается многочленом X1 + X2 +1. Функция f5
является монотонной, а f3 - нет, так как f3(0,1,1)=0 < 1=f3(0,1,0).
. Функция f3 является самодвойственной, а f2 - нет, так как f2(0,0,0) = f2(1,1,1). Функция f2 является линейной - она задается многочленом X1 + X2 +1. Функция f5
является монотонной, а f3 - нет, так как f3(0,1,1)=0 < 1=f3(0,1,0).
Теорема 5.1. Классы 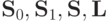 и
и  являются замкнутыми.
являются замкнутыми.
Доказательство. Замкнутость всех указанных классов устанавливается индукцией по построению
формул. Пусть 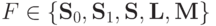 и
и ![f \in [F]](/sites/default/files/tex_cache/2b730aa05cf04a59f3f94dfa67b5d483.png) задается некоторой формулой над F.
Нужно показать, что тогда
задается некоторой формулой над F.
Нужно показать, что тогда  .
.
Базис индукции, когда эта формула есть переменная 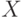 ,
очевиден.
,
очевиден.
Пусть f(X1, ..., Xk)= g(f1(X1, ..., Xk),
..., fn(X1, ..., Xk)),
и функции 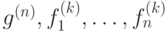 входят в F.
Требуется показать, что тогда и f входит в F.
входят в F.
Требуется показать, что тогда и f входит в F.
Для 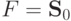 это просто:
это просто:
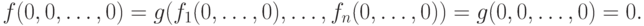
Аналогично проверяется случай 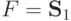 .
.
Если 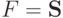 и
и 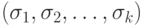 - произвольный набор аргументов, то
- произвольный набор аргументов, то

Следовательно, 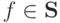 .
.
Пусть 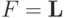 . Так как тогда g(n) и все
. Так как тогда g(n) и все 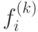 линейны, то существуют коэффициенты
линейны, то существуют коэффициенты 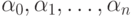 и
и 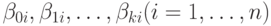 такие, что
такие, что 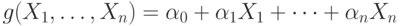 и
и 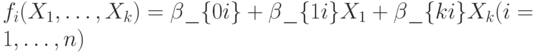 .
.
Подставив эти выражения в формулу для 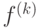 , получим
, получим
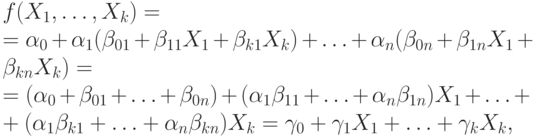
где 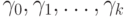 - значения
сумм констант в соответствующих скобках.
- значения
сумм констант в соответствующих скобках.
Следовательно, 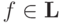 .
.
Наконец рассмотрим класс монотонных функций. Если 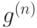 и все
и все 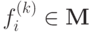 и
и 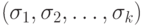 и
и 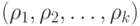 - два набора аргументов такие, что для всех
- два набора аргументов такие, что для всех ![j \in [1,k] \sigma _{j} \ge \rho _{j}](/sites/default/files/tex_cache/7e4b53cc9246ca3a8c37467e328b23e5.png) , то
, то

и поэтому
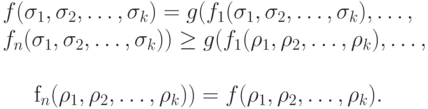
Таким образом, 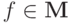 .
.

![F \subseteq [F]](/sites/default/files/tex_cache/db76450c14ac2abb88617f602098d474.png) .
.![F \subseteq G \Rightarrow [F] \subseteq [G]](/sites/default/files/tex_cache/e7b81aa88503c0ad4937fac9b9c3f9ab.png) .
.![F \subseteq [G]](/sites/default/files/tex_cache/be35d6951d84c9591e4171fe543e0d89.png) , то и система
, то и система 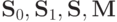 и
и