Иерархия сложностных классов
Иерархия сложностных классов
Напомним, что мы отождествляем языки и предикаты, как описано в
"Что такое алгоритм?"
. В частности, запись 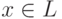 означает
означает 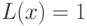 .
.
Определение 4.1. Пусть  — некоторый класс языков. Класс дополнений
— некоторый класс языков. Класс дополнений 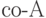 составляют дополнения ко всем языкам из
составляют дополнения ко всем языкам из  . Формально
. Формально
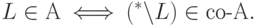
Непосредственно из определений классов 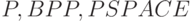 следует, что
следует, что 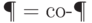 ,
,  ,
,  .
.
Игры, в которые играют машины.
Рассмотрим игру, в которую играют два игрока, будем их называть белые (Б) и черные (Ч). Игрокам сообщается некоторое слово  , и они делают ходы по очереди (
, и они делают ходы по очереди (  — первый ход белых,
— первый ход белых,  — первый ход черных и т.д.). Каждый ход может быть описан словом длины
— первый ход черных и т.д.). Каждый ход может быть описан словом длины 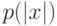 , где
, где 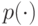 — некоторый полином. Игра завершается после некоторого, заранее заданного, числа ходов1. На самом деле правило завершения игры может быть и сложнее. Если есть верхняя оценка на число ходов, то можно всегда дополнить число ходов до этой оценки, никак не учитывая дополнительные ходы при подведении результата игры. Результат игры описывается некоторым предикатом
— некоторый полином. Игра завершается после некоторого, заранее заданного, числа ходов1. На самом деле правило завершения игры может быть и сложнее. Если есть верхняя оценка на число ходов, то можно всегда дополнить число ходов до этой оценки, никак не учитывая дополнительные ходы при подведении результата игры. Результат игры описывается некоторым предикатом 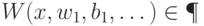 , истинность которого означает, что выиграли белые (ничьих не бывает, так что ложность
, истинность которого означает, что выиграли белые (ничьих не бывает, так что ложность  означает, что выиграли черные). Предикат
означает, что выиграли черные). Предикат  зависит от исходного слова и ходов, сделанных игроками:
зависит от исходного слова и ходов, сделанных игроками: 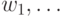 — белыми,
— белыми, 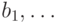 — черными. Поскольку
— черными. Поскольку 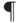 замкнут относительно дополнений, предикат
замкнут относительно дополнений, предикат 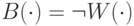 , утверждающий выигрыш черных, также принадлежит
, утверждающий выигрыш черных, также принадлежит 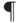 .
.
Отсутствие ничьих и конечность числа ходов гарантируют при заданном  существование выигрышной стратегии либо для белых, либо для черных. (Формальное доказательство легко получается индукцией по числу ходов.) Поэтому каждой игре можно сопоставить два взаимно дополнительных множества
существование выигрышной стратегии либо для белых, либо для черных. (Формальное доказательство легко получается индукцией по числу ходов.) Поэтому каждой игре можно сопоставить два взаимно дополнительных множества
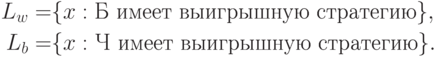
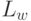 (или
(или 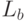 ), соответствующие тем или иным видам игр. Например, получаем следующие классы.
), соответствующие тем или иным видам игр. Например, получаем следующие классы. : множества
: множества 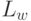 (как и
(как и 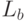 , впрочем) для игр, в которых никто не делает ходов.
, впрочем) для игр, в которых никто не делает ходов.
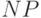 : множества
: множества 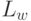 для игр, в которых белые делают 1 ход. Другими словами, это множества вида
для игр, в которых белые делают 1 ход. Другими словами, это множества вида
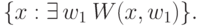
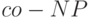 : множества
: множества 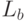 для игр, в которых белые делают 1 ход. Другими словами, это множества вида
для игр, в которых белые делают 1 ход. Другими словами, это множества вида
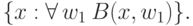
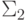 : множества
: множества 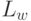 для игр из 2 ходов: 1 ход белых, 1 ход черных. Другими словами, это множества вида
для игр из 2 ходов: 1 ход белых, 1 ход черных. Другими словами, это множества вида
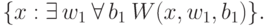
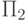 : множества
: множества 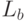 для игр из 2 ходов. Другими словами, это множества вида
для игр из 2 ходов. Другими словами, это множества вида
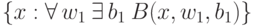

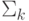 : множества
: множества 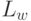 для игр из
для игр из  ходов (в зависимости от четности
ходов (в зависимости от четности  последними ходят либо черные, либо белые). Другими словами, это множества вида
последними ходят либо черные, либо белые). Другими словами, это множества вида
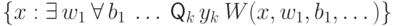
 четное, то
четное, то  ,
,  , если
, если  нечетное, то
нечетное, то  ,
, 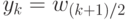 ).
).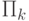 : множества
: множества 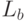 для игр из
для игр из  ходов (в зависимости от четности
ходов (в зависимости от четности  последними ходят либо черные, либо белые). Другими словами, это множества вида
последними ходят либо черные, либо белые). Другими словами, это множества вида
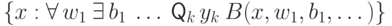
 четное, то
четное, то  ,
,  , если
, если  нечетное, то
нечетное, то  ,
, 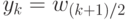 ).
).
Классы 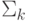 и
и 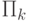 взаимно дополнительны:
взаимно дополнительны: 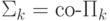 ,
, 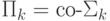 .
.
Теорема 4.1 (Лаутеман [35]). 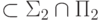 .
.
Доказательство. Поскольку класс BPP замкнут относительно дополнений, достаточно показать, что 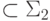 .
.
Для этого нужно научиться формулировать свойство "множество содержит много элементов" с использованием кванторов существования и всеобщности. Мы сделаем это, предполагая, что рассматриваются подмножества некоторой конечной группы. Пусть  — группа, а
— группа, а  — подмножество
— подмножество  . Свойство, которым мы будем отличать большие множества от малых, состоит в том, что некоторым количеством сдвигов множества
. Свойство, которым мы будем отличать большие множества от малых, состоит в том, что некоторым количеством сдвигов множества  можно покрыть всю группу
можно покрыть всю группу
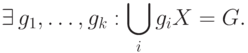 |
( 4.1) |
Чтобы выбрать подходящее значение  , нужно найти случаи, когда (4.1) заведомо выполняется, и когда заведомо не выполняется.
, нужно найти случаи, когда (4.1) заведомо выполняется, и когда заведомо не выполняется.
Если
 |
( 4.2) |
Условие (4.1) заведомо истинно, если для случайных независимых 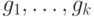 вероятность события
вероятность события 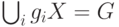 больше 0. Другими словами,
больше 0. Другими словами, ![\Prob[G\setminus\big( \bigcup_i g_iX\big)\ne\emptyset]<1](/sites/default/files/tex_cache/8643af0c6e5029ceabb6b3062629e812.png) . Вероятность того, что случайный сдвиг
. Вероятность того, что случайный сдвиг  не покрывает (не содержит) некоторый фиксированный элемент, равна по очевидным причинам
не покрывает (не содержит) некоторый фиксированный элемент, равна по очевидным причинам  . Вероятность того, что
. Вероятность того, что  случайных сдвигов не покрывают фиксированный элемент, равна
случайных сдвигов не покрывают фиксированный элемент, равна 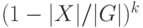 (покрытия разными сдвигами — независимые события). Поскольку покрывается
(покрытия разными сдвигами — независимые события). Поскольку покрывается 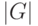 элементов, вероятность события
элементов, вероятность события ![\Prob[G\setminus\big( \bigcup_i g_iX\big)\ne\emptyset]](/sites/default/files/tex_cache/bbebb8b3a266e675f2fb0d999601618d.png) не больше
не больше 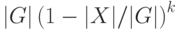 (вероятность объединения событий не больше суммы вероятностей этих событий). Итак, при
(вероятность объединения событий не больше суммы вероятностей этих событий). Итак, при
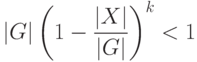 |
( 4.3) |
Рассмотрим теперь некоторый язык 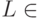 . Для него, как объяснялось выше, можно найти полиномиально вычислимый предикат
. Для него, как объяснялось выше, можно найти полиномиально вычислимый предикат 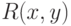 и полином
и полином 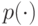 такие, что число
такие, что число 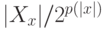 , где
, где 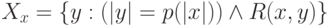 , различает слова, принадлежащие языку (для них оно больше
, различает слова, принадлежащие языку (для них оно больше 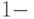 ), и слова, языку не принадлежащие (для таких слов это число меньше
), и слова, языку не принадлежащие (для таких слов это число меньше 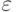 ). Параметр
). Параметр 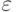 мы выберем позже, сейчас отметим, что его величина может быть экспоненциально мала, как объяснялось
"Вероятностные алгоритмы и класс BPP. Проверка простоты числа"
после определения 3.1.
мы выберем позже, сейчас отметим, что его величина может быть экспоненциально мала, как объяснялось
"Вероятностные алгоритмы и класс BPP. Проверка простоты числа"
после определения 3.1.
Введем искусственно структуру группы на множестве слов  длины
длины 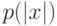 так, чтобы произведение и обращение элемента в этой группе были полиномиально вычислимыми (например, в качестве групповой операции возьмем покомпонентное сложение по модулю два). Запишем следующее
так, чтобы произведение и обращение элемента в этой группе были полиномиально вычислимыми (например, в качестве групповой операции возьмем покомпонентное сложение по модулю два). Запишем следующее 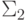 -условие
-условие
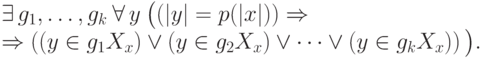
 слов (элементов группы), а черные — один элемент, который, по их мнению, не покрыт сдвигами множества
слов (элементов группы), а черные — один элемент, который, по их мнению, не покрыт сдвигами множества 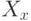 на слова
на слова  , названные белыми.
, названные белыми.Условие (4.2) в этом случае имеет вид  , а условие (4.3):
, а условие (4.3): 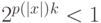 . Эти условия выполняются при подходящем выборе параметров. Можно взять
. Эти условия выполняются при подходящем выборе параметров. Можно взять  порядка
порядка 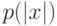 и
и 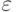 порядка
порядка 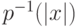 .
.
Замечание 4.1. Имеется рассуждение, которое "показывает", что время вычисления функций из класса BPP можно сделать, по-видимому, меньше  для любого
для любого 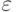 . Идея состоит в том, чтобы использовать генераторы псевдослучайных чисел. Такой генератор по набору битов длины
. Идея состоит в том, чтобы использовать генераторы псевдослучайных чисел. Такой генератор по набору битов длины  строит набор длины
строит набор длины 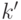 , где
, где  . Если при этом выбирать короткие наборы случайно, то длинные наборы будут распределены так, что вычислительное устройство с ограниченными ресурсами (например, полиномиальная машина Тьюринга) не сможет отличить их от по-настоящему случайных. Это пояснение заменяет точное определение псевдослучайного генератора, которое нам не понадобится.
. Если при этом выбирать короткие наборы случайно, то длинные наборы будут распределены так, что вычислительное устройство с ограниченными ресурсами (например, полиномиальная машина Тьюринга) не сможет отличить их от по-настоящему случайных. Это пояснение заменяет точное определение псевдослучайного генератора, которое нам не понадобится.
Существуют ли псевдослучайные генераторы, неизвестно. Их заведомо нет, если  . Но в этом случае
. Но в этом случае 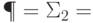 .
.
Если же  и есть псевдослучайные генераторы, то можно находить за указанное выше время значение функции
и есть псевдослучайные генераторы, то можно находить за указанное выше время значение функции 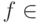 , вычисляя значения предиката
, вычисляя значения предиката 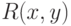 из опр. 3.2 только для псевдослучайных
из опр. 3.2 только для псевдослучайных  .
.
Остается "небольшой" дефект в этом рассуждении: оно не проходит при  и отсутствии псевдослучайных генераторов. Такая ситуация считается маловероятной.
и отсутствии псевдослучайных генераторов. Такая ситуация считается маловероятной.
