|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Многозначные отображения и транзитивные замыкания
Многозначные отображения
Прямые отображения
Прямым отображением 1-го порядка вершины хi является множество таких вершин графа, для которых существует дуга (хi, xj), т. е 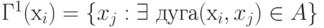 для графа G = (X, A), где X ={ хi }, i =1, 2, ..., n – множество вершин, а A = {ai}, i =
= 1, 2, ..., m – множество дуг.
для графа G = (X, A), где X ={ хi }, i =1, 2, ..., n – множество вершин, а A = {ai}, i =
= 1, 2, ..., m – множество дуг.
Прямое отображение 2-го порядка вершины хi – это прямое отображение от прямого отображения 1-го порядка, т. е. Г+2( хi ) = Г+( Г+1 ( хi ) ).
Аналогично можно записать для прямого отображения 3-го и т. д. n -го порядка.
Г+3(xi)= Г+(Г+2(xi))= Г+(Г+(Г+1(xi)))
...
Г+n(xi)=Г+(Г+(n-1)(xi)).
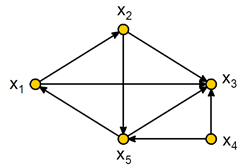
Прямые многозначные отображения для графа на рис. 3.1 находятся следующим образом:
Г+1(x1)=(x2,x3),
Г+2(x1)=Г+(Г+1(x1))=Г+(x2,x3)=(x3,x5),
Г+3(x1)=Г+(Г+2(x1))=Г+(x3,x5)=(x3,x1) и т. д.
Обратные отображения
Обратным отображением 1-го порядка для вершины хi является множество элементов xj таких, что существует дуга (xj, хi), принадлежащая множеству дуг графа, т. е.  .
.
Обратные отображения 2-го, 3-го и т. д. n -го порядка определяются следующим образом:
Г-2(xi)= Г-(Г-1(xi)),
Г-3(xi)= Г-(Г-2(xi)),
...
Г-n(xi)= Г-(Г(n-1)(xi)).
Для графа на рис. 3.1 обратные многозначные отображения вершины х1 находятся следующим образом:
Г-1(x1)=x5,
Г-2(x1)= Г-(Г-1(x1))=Г-(x5)= x2,x4,
Г-3(x1)= Г-(Г-2(x1))=Г-(x2x4)= x1,
Г-4(x1)= Г-(Г-3(x1))=Г-(x1)= x5 и т.д.
П р и м е ч а н и я:
1. Когда отображение действует не на одну вершину, а на множество вершин Хq = { х1, х2, ..., хq }, то под Г(Хq) понимают объединение
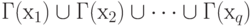 .
.
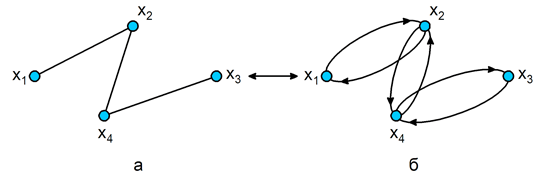
2. Многозначное отображение для неориентированного графа строится, если представить каждое ребро двумя противоположно направленными дугами ( рис. 3.2).