|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Типы графов
Граф G = (X, A) называют полным, если для любой пары вершин хi и хj в X существует ребро (хi, хj) в неориентированном графе
G=(X,A)
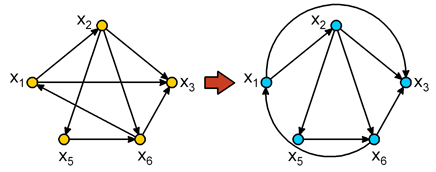
т. е. для каждой пары вершин графа G должна существовать по крайней мере одна дуга, соединяющая их ( рис. 5.1,а).
Граф G =(X, A) называется симметрическим, если в множестве дуг A для любой дуги (хi, хj) существует также противоположно ориентированная дуга (хj, хi) ( рис. 5.1,б).
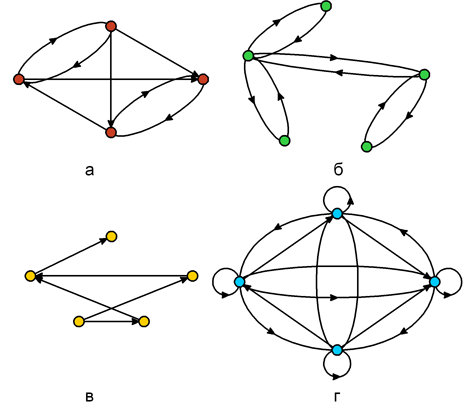
Рис. 5.1. а – полный граф; б – симметрический граф; в – антисимметрический граф; г – полный симметрический;
Антисимметрическим называется такой граф, для которого справедливо следующее условие: если 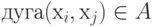 , то во
множестве A нет противоположно ориентированной дуги, т. е.
(
, то во
множестве A нет противоположно ориентированной дуги, т. е.
( 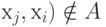 (
рис.
5.1,в). Очевидно, что в антисимметрическом графе нет петель.
(
рис.
5.1,в). Очевидно, что в антисимметрическом графе нет петель.
В качестве примера можно рассмотреть граф, являющийся моделью некоторой группы людей: вершины графа интерпретируют людей, а дуги – их взаимоотношения. Так, если в графе дуга, нарисованная от вершины хi к вершине хj , означает, что хi является другом или родственником хj , тогда данный граф должен быть симметрическим. Если дуга, направленная от хi к хj , означает, что вершина хj подчинена вершине хi , то такой граф должен быть антисимметрическим.
Комбинируя определения полного и симметрического графов и полного и антисимметрического графов, получили следующие определения:
- граф G =(X, A), в котором любая пара вершин (хi, хj) соединена двунаправленными дугами, называется полным симметрическим ( рис. 5.1,г). Очевидно, что в полном симметрическом графе каждая вершина имеет петлю;
- граф G =(X, A), имеющий для каждой пары вершин (хi, хj) только одну дугу, называется полным антисимметрическим или турниром.
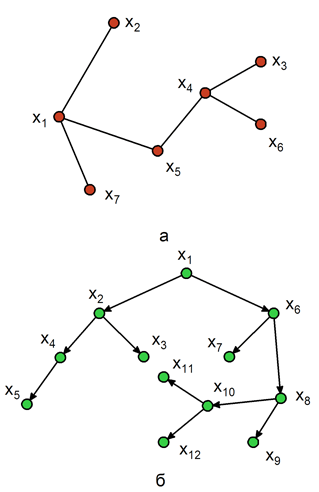
Связный граф, не имеющий циклов, либо граф, в котором каждая пара вершин соединена одной и только одной простой цепью, называется деревом ( рис. 5.2, а, б).
Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины, за исключением одной (например, вершины х1 ), равна 1, а полустепень захода вершины х1 (называют корнем этого дерева) равна 0 ( рис. 5.2,б).
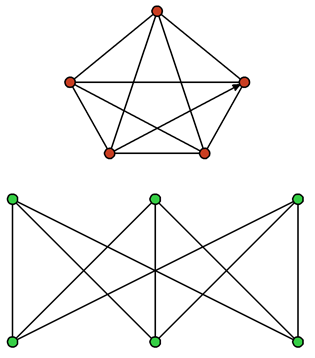
Граф G =(X, A), который может быть изображен на плоскости или сфере без пересечений называется планарным ( рис. 5.3).
На рис. 5.4 показаны непланарные графы. Эти два графа играют важную роль в теории планарных графов и известны как графы Куратовского.
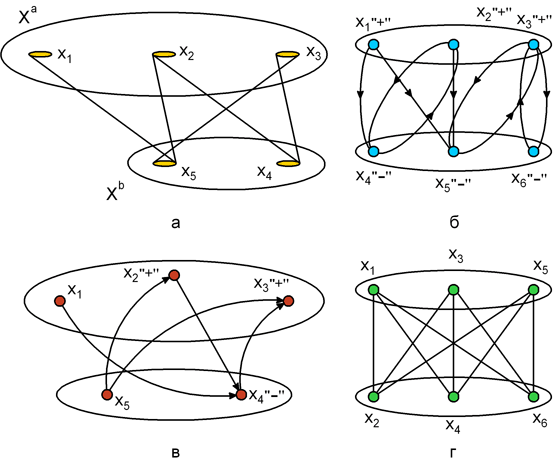
Неориентированный граф G = (X, A) называют двудольным, если множество его вершин X может быть разбито на такие два подмножества Xа и Xb , что каждое ребро имеет один конец в Xа , а другой в Xb ( рис. 5.5,а).
Ориентированный граф G называется двудольным, если его неориентированный двойник – двудольный граф ( рис. 5.5,б,в).
Двудольный граф  называют полным, если для любых двух вершин
называют полным, если для любых двух вершин 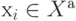 и
и  существует ребро (хi,хj) в G=(X,A) (
рис.
5.5,г).
существует ребро (хi,хj) в G=(X,A) (
рис.
5.5,г).
Для доказательства двудольности графа существует теорема.