|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Лекция 7: Методы разбиения графа на максимальные сильно связные подграфы
Метод Мальгранжа
Пусть дан граф G=(X, A), где X={ хi }, i =1, 2, ... , n – множество вершин, а A={ ai }, i =1, 2, ..., m – где множество дуг, описанных матрицей смежности. Алгоритм разбиения заключается в следующем [4].
- Для произвольной вершины
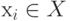 находим прямое T+(хi) и обратное T-(хi) транзитивные замыкания.
находим прямое T+(хi) и обратное T-(хi) транзитивные замыкания. - Находим
 . Множество вершин этого пересечения составляют вершины максимального сильно связного подграфа G1 = (Х1, A1).
. Множество вершин этого пересечения составляют вершины максимального сильно связного подграфа G1 = (Х1, A1). - Из исходного графа вычитаем подграф G1:G '=G\G1, Х'=X\Х1 .
- Граф G ' принимаем за исходный граф и пока
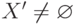 пункты 1, 2, 3 алгоритма повторяются.
пункты 1, 2, 3 алгоритма повторяются.
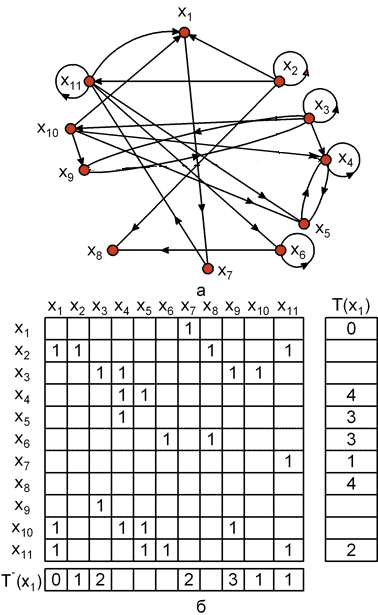
Рассмотрим этот алгоритм более подробно на примере разбиения графа, представленного на рис. 7.1,a, матрица смежности которого показана на рис. 7.1,б.
РАЗБИЕНИЕ – 1 .
-
Начальной вершиной первого разбиения выберем х1 . Построим прямое и обратное транзитивные замыкания. T+(х1) – столбец, показанный справа от матрицы А, а T-(х1) – строка, находящаяся ниже матрицы смежности.
T+(х1) = {х1, х4, х5, х6, х7, х8, х11 },
T-(х1) = {х1, х2, х3, х7, х9, х10, х11}.
- Находим
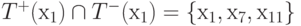 . Эти вершины и составляют первый выделенный, максимальный сильно связный подграф G1 = (Х1, A1), где Х1 = {х1, х7, х11}, а матрица смежности A1
подграфа G1
показана на
таблица
7.1.
. Эти вершины и составляют первый выделенный, максимальный сильно связный подграф G1 = (Х1, A1), где Х1 = {х1, х7, х11}, а матрица смежности A1
подграфа G1
показана на
таблица
7.1. -
Из исходного графа G вычитаем подграф G1 G ' = G \G1 ;
G ' = (X ', A'), X ' = { х2, х3, х4, х5, х6, х8, х9, х10 }.
- Так как X ' не пустое множество, то G' принимаем за G и переходим ко второму разбиению.
РАЗБИЕНИЕ – 2
| X2 | X3 | X4 | X5 | X6 | X8 | X9 | X10 | T+(x2) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X2 | 1 | 1 | 0 | ||||||||
| X3 | 1 | 1 | 1 | 1 | |||||||
| X4 | 1 | 1 | |||||||||
| X5 | 1 | ||||||||||
| A= | X6 | 1 | 1 | ||||||||
| X8 | 1 | ||||||||||
| X9 | 1 | ||||||||||
| X10 | 1 | 1 | 1 | ||||||||
| T-(x2) | 0 |
- Выбираем любую вершину, принадлежащую X, например, х2 , и находим T+(х2) и T-(х2). Это показано в таблице 7.2. T+(х2) = { х2, х8 } ; T-(х2) = { х2 }.
-
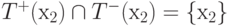 . Следовательно, второй выделенный подграф G2
состоит из одной вершины х2
.
. Следовательно, второй выделенный подграф G2
состоит из одной вершины х2
. - G ' = G \G2; G ' = (X ', A'); X ' = { х3, х4, х5, х6, х8, х9, х10 }.
- Так как X ' не пустое множество, то G ' принимаем за G и процесс разбиения продолжается.