|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Лекция 9: Алгоритм Дейкстра поиска кратчайших путей в графе
Наиболее эффективный алгоритм решения задачи о кратчайшем пути первоначально дал Дейкстра. В общем случае этот метод основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины пути от некоторой вершины s к рассматриваемой вершине. Эти пометки постепенно уменьшаются с помощью некоторой итерационной процедуры, и на каждом шаге итерации только одна из временных пометок становится постоянной. Последнее указывает на то, что пометка уже не является верхней границей, а дает точную длину кратчайшего пути от t к рассматриваемой вершине. Рассмотрим подробнее этот алгоритм.
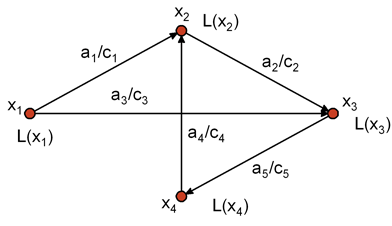
Дан граф G = (X, A, C) со взвешенными дугами, пример которого показан на рис. 9.1 Обозначим L(хi) пометку вершины хi . Веса дуг (или ребер) даны матрицей весов ( таблица 9.1).
Рассмотрим алгоритм нахождения кратчайшего пути от вершины s к вершине t графа и более общий случай: от вершины s ко всем вершинам графа.
Присвоение начальных значений
Ш А Г 1. Положить L(s) = 0 и считать эту пометку постоянной. Для всех вершин 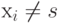 положить
положить 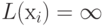 и считать эти пометки временными. За текущую рассматриваемую вершину с постоянной пометкой возьмем вершину p, т. е. положить p = s.
и считать эти пометки временными. За текущую рассматриваемую вершину с постоянной пометкой возьмем вершину p, т. е. положить p = s.
Обновление пометок
Ш А Г 2. Для вершин, входящих в прямое отображение вершины р, т. е. для всех хi , принадлежащих Г(p), пометки которых временные, изменить пометки в соответствии со следующим выражением:
L(хi) <- min [ L(хi), L(p) + C(p, хi) ].
Превращение пометки в постоянную
Ш А Г 3. Среди всех вершин с временными пометками найти такую, для которой
L(x*i)=min[L(xi)].
Ш А Г 4. Считать пометку вершины x*i постоянной и положить p=x*i.
Ш А Г 5(a ). { При нахождении пути от s к t }
- Если текущая вершина p является искомой, т. е. p = t, то L(p) является длиной кратчайшего пути от s к t. Останов.
- Если
 , перейти к шагу 2.
, перейти к шагу 2.
Ш А Г 5(б). { При нахождении путей от s ко всем вершинам }
- Если все вершины отмечены постоянными метками, то эти метки дают длины кратчайших путей.
- Если некоторые метки являются временными, то следует перейти к шагу 2.
Как только длины кратчайших путей от вершины s будут найдены, сами пути можно получить с помощью рекурсивной процедуры ( * ). Так как вершина x*i непосредственно предшествует вершине хi в кратчайшем пути от s к хi , то для любой вершины хi соответствующую вершину x*i можно найти как одну из оставшихся вершин, для которой
L(x*i)+c( x*i, xi)=L( xi).(*)
Если кратчайший путь от s до любой вершины хi является единственным, то дуги (x*i, xi) этого кратчайшего пути образуют ориентированное дерево с корнем s. Если существует несколько кратчайших путей от s к какой-либо другой вершине, то при некоторой фиксированной вершине x*i соотношение ( * ) будет выполняться для более чем одной вершины хi . В этом случае выбор может быть либо произвольным (если нужен какой-то один кратчайший путь между s и хi ), либо таким, что рассматриваются все дуги (x*2,x2), входящие в какой-либо из кратчайших путей, и при этом совокупность всех таких дуг образует не ориентированное дерево, а общий граф, называемый базой относительно s.
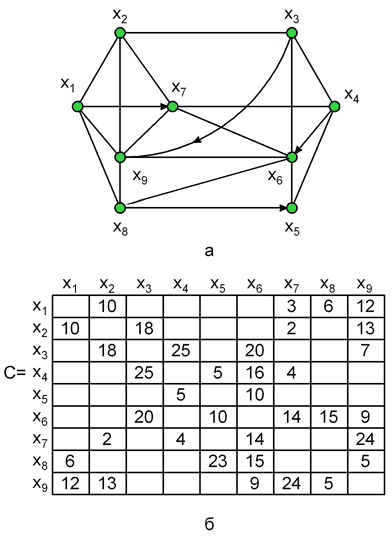
П р и м е р. Рассмотрим граф смешанного типа, изображенный на рис. 9.2,а, где каждое неориентированное ребро рассматривается как пара противоположно направленных дуг равного веса. Матрица весов приведена на рис. 9.2,б. Требуется найти все кратчайшие пути от вершины х1 ко всем остальным вершинам.
Постоянные пометки будем помечать знаком +.
Ш А Г 1. Присвоим 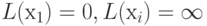 для всех хi
, кроме х1
. Положим р = х1
.
для всех хi
, кроме х1
. Положим р = х1
.
Первая итерация
Ш А Г 2. Найдем прямое отображение для текущей рассматриваемой вершины: Г(р) = Г(х1) = { х2, х7, х8, х9 }. Все вершины, входящие в прямое отображение имеют временные пометки, поэтому пересчитаем их значение:
![L(x_{2})=min[L(x_{2}),L(x_{1}) + c(x_{1},x_{2})]=min[\infty ,0+10]=10](/sites/default/files/tex_cache/625a7e428560b138d634c3cf57f45afa.png)
![L(x_{7})=min[\infty ,0+3]=3](/sites/default/files/tex_cache/6b6d336770f315780c981180b4eefff1.png)
![L(x_{8})=min[\infty ,0+6]=6](/sites/default/files/tex_cache/5898cea8c9e5cab5c480ad85f61a993f.png)
![L(x_{9})=min[\infty ,0+12]=12](/sites/default/files/tex_cache/31ee500d2de47f147f2205a425d88003.png)
Ш А Г 3. На данном шаге итерации имеем следующие временные метки вершин:
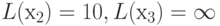 ,
,
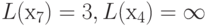 ,
,
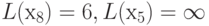 ,
,
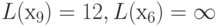 .
.
Очевидно, что минимальную метку, равную 3, имеет вершина х7 .
Ш А Г 4. За следующую текущую метку принимаем вершину х7 , т. е. p = х7 , а ее метка становится постоянной, L(х7) = 3+ .
Ш А Г 5. Так как не все вершины графа имеют постоянные метки, переходим к шагу 2.