Графы и способы их представления

Введение

В последние годы особую важность приобрели те разделы математики, которые имеют отношение к развитию цифровых устройств, цифровой связи и цифровых вычислительных машин. Базой для преподавания этих дисциплин наряду с классическими методами анализа непрерывных физических моделей стали алгебраические, логические и комбинаторные методы исследования различных моделей дискретной математики.

Значительно возросла популярность теории графов – ветви дискретной математики. Графы встречаются во многих областях под разными названиями: "структуры" в гражданском строительстве, "сети" – в электронике, "социограммы" – в социологии и экономике, "молекулярные структуры" – в химии, "дорожные карты", электрические или газовые распределительные сети и т. д.

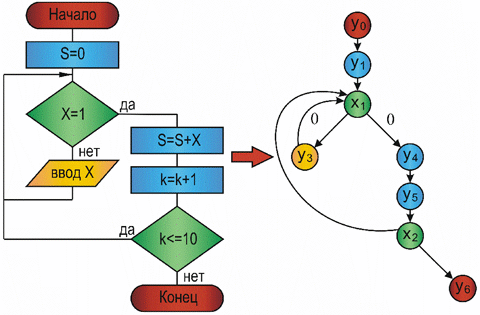
Родившись при решении головоломок и игр, таких, например, как задача о кенигсбергских мостах и игра Гамильтона, теория графов стала мощным средством исследования и решения многих задач, возникающих при изучении больших и сложных систем. Для специалистов по вычислительной технике, информационным системам и системам цифровой связи теория графов – это удобный язык выражения понятий из этой области; многие результаты теории графов имеют непосредственную связь с задачами, с которыми им приходится сталкиваться. Графическая интерпретация различных моделей графов дана на рис. 1.1 Так в виде ориентированных графов можно представить любую логическую или функционально - логическую схему ( рис. 1.1,а). На таких графовых моделях можно, например, оценить быстродействие схемы. Блок-схема алгоритма может быть представлена вероятностным графом ( рис. 1.1,б), который позволяет оценить временные характеристики алгоритма, затраты процессорного времени, трудоемкость и другие. Графом типа "дерево" можно отобразить практически любую структуру организации или предприятия ( рис. 1.1,в).

Широкое применение теория графов получила при исследовании так называемой проблемы оптимизации, возникающей при конструировании больших систем как технических, так и программных, например, таких, как компиляторы.

В рамках этих исследований были разработаны многие, неизвестные ранее теоретико-графовые понятия. Теория графов имеет большую привлекательность для специалистов в области проектирования для построения эффективных алгоритмов и анализа их сложности. Использование аппарата теории графов оказало существенное влияние на разработку алгоритмов конструкторского проектирования схем. Непосредственное и детальное представление практических систем, таких, как распределительные сети, системы связи, приводит к графам большого размера, успешный анализ которых зависит в равной степени, как от эффективных алгоритмов, так и от возможностей компьютерной техники. Поэтому в настоящее время основное внимание сосредоточено на разработке и описании компьютерных алгоритмов анализа графов. В связи с этим основной упор в данном учебном пособии делается на машинные способы представления графов и алгоритмы решения задач на графах, легко реализуемых на ЭВМ.

a

б

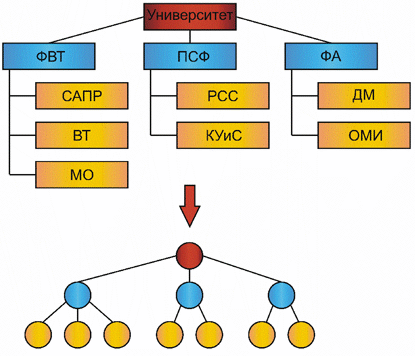
Рис. 1.1. Графическая интерпретация применения графовых структур: а – орграф; б – вероятностный граф; в – граф-дерево

Графы и способы их представления

Основные определения

Граф задается множеством точек или вершин х₁, х₂, ..., х_n и множеством линий или ребер a₁, a₂, ... , a_m, соединяющих между собой все или часть точек. Формальное определение графа может быть дано следующим образом.

Графом называется двойка вида

G = (X, A),

где X = {x_i}, i = 1, 2, ..., n – множество вершин графа, A = {a_i}, i = 1, 2,... , m – множество ребер графа.

Графы могут быть ориентированными, неориентированными и смешанными ( рис. 1.2). Если ребра у множества A ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным графом или орграфом ( рис. 1.2,а).

Рис. 1.2.

Если ребра не имеют ориентации, то граф называется неориентированным ( рис. 1.2,б). Граф, в котором присутствуют и ребра, и дуги называется смешанным ( рис. 1.2,в). В случае, когда G = (X, A) является орграфом, и мы хотим пренебречь направленностью дуг из множества A, то неориентированный граф, соответствующий G, будет обозначаться и называться неориентированным дубликатом или неориентированным двойником ( рис. 1.2,г).

Дуга a_i может быть представлена упорядоченной парой вершин (х_n, х_k), состоящей из начальной х_n и конечной х_k вершин. Например, для графа G₁ ( рис. 1.2,а) дуга a₁ задается парой вершин (x₂, x₁), а дуга а₃ парой (x₂, x₃). Если х_n, х_k – концевые вершины дуги a_i, то говорят, что вершины х_n и х_k инцидентны дуге a_i или дуга a_i инцидентна вершинам х_n и х_k.

Дуга, у которой начальная и конечная вершины совпадают, называется петлей. В графе G₃ ( рис. 1.2,в) дуга a₇ является петлей.

Каждая вершина орграфа х_i может характеризоваться полустепенью исхода d₀(х_i) и полустепенью захода d_t(х_i).

Полустепенью исхода вершины х_i — d₀(х_i) называется количество дуг, исходящих из этой вершины. Например, для графа G₁ ( рис. 1.2,а) характеристики полустепеней исхода следующие: d₀(х₁)=1, d₀(х₂)=2, d₀(х₃)=2, d₀(х₄ )=1.

Полустепенью захода вершины х_i — d_t(х_i) называется количество дуг, входящих в эту вершину. Например, для орграфа G₁: d_t(х₁)=2, d_t(х₂)=1, d_t(х₃)=2, d_t(х₄ )=1.

Очевидно, что сумма полустепеней исхода всех вершин графа, а также сумма полустепеней захода всех вершин графа равна общему числу дуг графа, т. е.

где n – число вершин графа, m – число дуг.

Каждая вершина неориентированного графа х_i может характеризоваться степенью вершины d(х_i).

Степенью вершины х_i – d(х_i) называется количество ребер, инцидентных этой вершине. Например, для орграфа G₁ ( рис. 1.2,б) характеристики степеней следующие: d(х₁)=2, d(х₂)=3, d(х₃)=3, d(х₄ )=2.