|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
9.22. ЛЕММА. Пусть  - свободный
- свободный  -модуль и
-модуль и  - конечное подмножество модуля
- конечное подмножество модуля  . Тогда отношение
редукции
. Тогда отношение
редукции 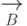 является
нетеровым, т.е. не существует бесконечных цепочек вида
является
нетеровым, т.е. не существует бесконечных цепочек вида 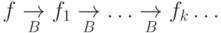 . Следовательно, для любого элемента
. Следовательно, для любого элемента  существует (не обязательно
единственный) нередуцируемый элемент
существует (не обязательно
единственный) нередуцируемый элемент 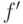 , такой, что
, такой, что 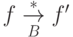 .
.
ДОКАЗАТЕЛЬСТВО.
Предположим противное. Всякий ранжир, по определению, вполне упорядочивает
множество термов 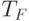 . Поэтому мы можем выбрать среди
всех бесконечных цепочек редукций цепочку, начинающуюся с элемента
. Поэтому мы можем выбрать среди
всех бесконечных цепочек редукций цепочку, начинающуюся с элемента  с минимальным относительно ранжира лидером
с минимальным относительно ранжира лидером  .
Возможны
две ситуации: либо на некотором шаге редукции терм
.
Возможны
две ситуации: либо на некотором шаге редукции терм  редуцируется
и оставшаяся часть цепочки начинается с элемента, все
слагаемые которого меньше, чем
редуцируется
и оставшаяся часть цепочки начинается с элемента, все
слагаемые которого меньше, чем  ; либо
; либо  не
редуцируется ни на каком шаге редукции. В обоих случаях получается
противоречие с
минимальностью выбранной цепочки: в первом случае можно выбрать хвост исходной
цепочки, остающийся после редуцирования
не
редуцируется ни на каком шаге редукции. В обоих случаях получается
противоречие с
минимальностью выбранной цепочки: в первом случае можно выбрать хвост исходной
цепочки, остающийся после редуцирования  ; во
втором - вычесть из всех элементов цепочки терм
; во
втором - вычесть из всех элементов цепочки терм  .
.
9.23. ПРЕДЛОЖЕНИЕ.
Множество нередуцируемых относительно отношения ![\smash[b]{\underset
B\to}](/sites/default/files/tex_cache/07c0665b2f040c0e6ea0f6c6908c0c2d.png) элементов является
векторным
элементов является
векторным  -пространством.
-пространством.
ДОКАЗАТЕЛЬСТВО.
Нужно проверить, что если  и
и  -
нередуцируемые элементы и
-
нередуцируемые элементы и 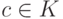 , то элементы
, то элементы  и
и 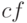 также нередуцируемы. Это
немедленно следует из того, что в
также нередуцируемы. Это
немедленно следует из того, что в  и
и 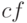 присутствуют с ненулевыми коэффициентами только те слагаемые, которые
присутствуют в
присутствуют с ненулевыми коэффициентами только те слагаемые, которые
присутствуют в  и
и  .
.
9.24. ЛЕММА. Если множество  порождает подмодуль
порождает подмодуль 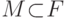 и
и 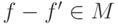 , то существует целое
, то существует целое 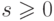 и элементы
и элементы  , такие, что для всех
, такие, что для всех  от 1 до
от 1 до  либо
либо 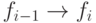 , либо
, либо 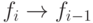 .
.
ДОКАЗАТЕЛЬСТВО.
Поскольку  порождает модуль
порождает модуль  , элемент
, элемент 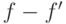 можно представить в виде суммы
можно представить в виде суммы
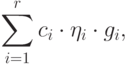
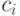 - коэффициенты,
- коэффициенты, 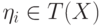 ,
, 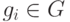 (могут совпадать при различных
значениях
(могут совпадать при различных
значениях  ). Доказательство леммы
будем вести индукцией по минимальной длине
). Доказательство леммы
будем вести индукцией по минимальной длине  такого
представления. Если
такого
представления. Если  , то
, то 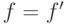 , и утверждение
леммы выполнено. Для
произвольного
, и утверждение
леммы выполнено. Для
произвольного  мы можем предполагать, что
мы можем предполагать, что 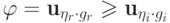 для всех
для всех  . Положим
. Положим 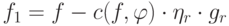 ,
, 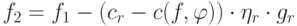 . Тогда
. Тогда 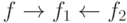 и
и 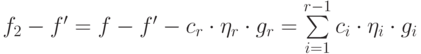 , так что
можно применить предположение индукции.
, так что
можно применить предположение индукции.9.25. ОПРЕДЕЛЕНИЕ.
На прямом произведении  определим функцию
определим функцию  , такую, что
, такую, что 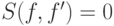 , если
, если 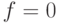 ,
или
,
или 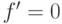 , или
, или 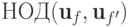 не определен; в
остальных случаях
не определен; в
остальных случаях 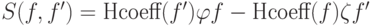 ,
где
,
где  и
и 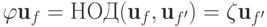 .
.
9.26. ОПРЕДЕЛЕНИЕ.
Пусть  - кольцо обобщенных многочленов от переменных
- кольцо обобщенных многочленов от переменных 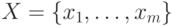 над полем
над полем  ,
,  - свободный
- свободный  -модуль. Предположим, что
-модуль. Предположим, что 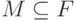 - подмодуль свободного модуля
- подмодуль свободного модуля  ,
, 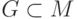 - конечное множество и < - ранжир на
множестве термов
- конечное множество и < - ранжир на
множестве термов 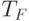 .
Множество
.
Множество  называется базисом Гребнера (
называется базисом Гребнера (  -базисом)
подмодуля
-базисом)
подмодуля  , если
для любого ненулевого элемента
, если
для любого ненулевого элемента 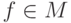 имеется представление Гребнера (
имеется представление Гребнера (  -представление):
-представление):
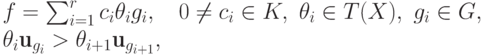
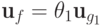 .
.Недостатком введенного определения является то, что для одного и
того же элемента могут существовать различные  -представления. Например, если
-представления. Например, если 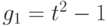 ,
, 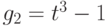 , то
, то 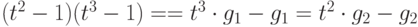 - два различных
- два различных  -представления одного и
того же
многочлена. С другой стороны, достаточно сложно проверить, что
некоторый элемент не допускает
-представления одного и
того же
многочлена. С другой стороны, достаточно сложно проверить, что
некоторый элемент не допускает  -представления. От этих
недостатков можно избавиться, если потребовать, чтобы любой
одночлен мог появляться в
-представления. От этих
недостатков можно избавиться, если потребовать, чтобы любой
одночлен мог появляться в  -представлении в качестве лидера
слагаемого
-представлении в качестве лидера
слагаемого 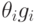 не более чем для одного элемента
не более чем для одного элемента 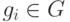 . В частности, можно предполагать, что элементы множества
. В частности, можно предполагать, что элементы множества  упорядочены, и при выборе линейно независимых элементов вида
упорядочены, и при выборе линейно независимых элементов вида 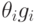 мы руководствуемся правилами, сформулированными в
определении нормальной редукции 9.19. Представление
такого вида мы будем называть нормальным
мы руководствуемся правилами, сформулированными в
определении нормальной редукции 9.19. Представление
такого вида мы будем называть нормальным  - представлением.
- представлением.
Для формулировки основного результата настоящего параграфа введем некоторые обозначения и докажем две леммы.
9.27. ОПРЕДЕЛЕНИЕ.
Для элементов 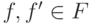 будем писать
будем писать 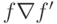 , если существует элемент
, если существует элемент 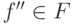 , такой, что
, такой, что  и
и  .
.
9.28. ЛЕММА.
Пусть 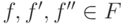 и
и  . Тогда
. Тогда 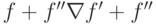 .
.
ДОКАЗАТЕЛЬСТВО.
Пусть 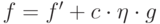 , где
, где 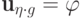 и
и 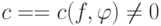 ,
, 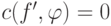 . Если
. Если  , то
, то 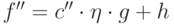 , где
, где  , тогда
, тогда
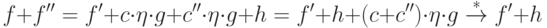
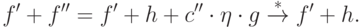
9.29. ОПРЕДЕЛЕНИЕ.
Будем говорить, что отношение редукции 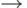 удовлетворяет условию слияния }, если для любого
элемента
удовлетворяет условию слияния }, если для любого
элемента  из условий
из условий  и
и  следует, что
следует, что  .
.
9.30. ОПРЕДЕЛЕНИЕ.
Будем говорить, что отношение редукции 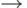 удовлетворяет локальному условию слияния, если для любого элемента
удовлетворяет локальному условию слияния, если для любого элемента  из
из 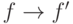 и
и 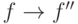 следует, что
следует, что  .
.
9.31. ОПРЕДЕЛЕНИЕ.
Будем говорить, что отношение редукции 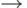 удовлетворяет псевдолокальному условию слияния, если для
всех
удовлетворяет псевдолокальному условию слияния, если для
всех 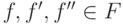 , таких, что
, таких, что 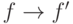 и
и 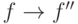 , существует
целое
, существует
целое 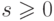 и элементы
и элементы 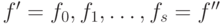 , такие, что
, такие, что  и
и  для всех
для всех 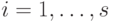 .
.
9.32. ЛЕММА. Если нетерово отношение 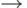 удовлетворяет псевдолокальному
условию слияния, то отношение
удовлетворяет псевдолокальному
условию слияния, то отношение 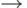 удовлетворяет условию слияния.
удовлетворяет условию слияния.
ДОКАЗАТЕЛЬСТВО.
Применим "нетерову" индукцию, т.е. покажем, что если утверждение леммы верно
для всех  таких, что
таких, что  , то оно
верно и для
, то оно
верно и для  . Такой индукции достаточно для доказательства
леммы, поскольку в противном случае некоторый элемент
. Такой индукции достаточно для доказательства
леммы, поскольку в противном случае некоторый элемент  , для
которого утверждение леммы не выполняется, мог бы быть выбран в качестве
первого элемента бесконечной цепочки
, для
которого утверждение леммы не выполняется, мог бы быть выбран в качестве
первого элемента бесконечной цепочки 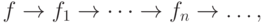 для всех элементов которой утверждение
леммы также не выполняется.
для всех элементов которой утверждение
леммы также не выполняется.
Итак, фиксируем  и предположим, что для всех элементов
и предположим, что для всех элементов 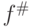 таких, что
таких, что  , утверждение
леммы выполняется.
Покажем, что оно выполняется и для
, утверждение
леммы выполняется.
Покажем, что оно выполняется и для  . Без потери общности мы
можем предполагать, что данные элементы
. Без потери общности мы
можем предполагать, что данные элементы 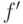 и
и 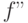 отличны от
отличны от  , т.е. имеют место редукции
, т.е. имеют место редукции 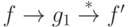 и
и 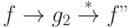 . Элементы
. Элементы 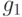 и
и  удовлетворяют
псевдолокальному условию слияния при некотором~
удовлетворяют
псевдолокальному условию слияния при некотором~  .
.
Доказательство будем вести индукцией по  . Основание индукции
по
. Основание индукции
по  предполагает
предполагает 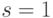 , т.е.
, т.е. 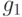 и
и  удовлетворяют
локальному условию слияния. Из условия локального слияния следует, что
существует
удовлетворяют
локальному условию слияния. Из условия локального слияния следует, что
существует  , такой, что
, такой, что  и
и  По предположению внешней индукции
для элементов
По предположению внешней индукции
для элементов 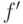 и
и  существует элемент
существует элемент  , такой, что
, такой, что  и
и  , а также элемент
, а также элемент 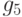 , такой,
что
, такой,
что  и
и  .
Этот элемент
удовлетворяет условию леммы (см.
рис.
6.1).
.
Этот элемент
удовлетворяет условию леммы (см.
рис.
6.1).
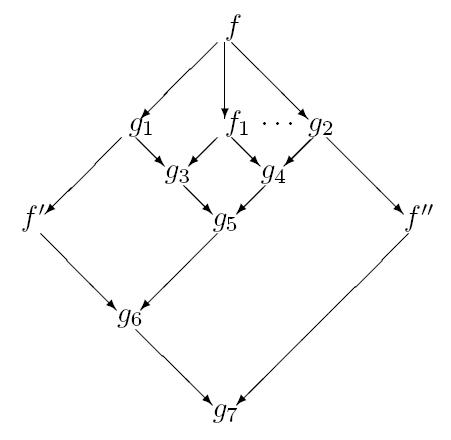
Переход от  к
к  иллюстрируется следующей
диаграммой (
рис.
6.2). Пусть
иллюстрируется следующей
диаграммой (
рис.
6.2). Пусть 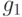 и
и  удовлетворяют псевдолокальному
условию слияния с цепочкой из
удовлетворяют псевдолокальному
условию слияния с цепочкой из  элементов:
элементов: 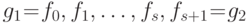 . По предположению индукции
элементы
. По предположению индукции
элементы 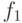 и
и  удовлетворяют условию слияния (элемент
удовлетворяют условию слияния (элемент  ). Существование элементов
). Существование элементов 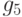 ,
, 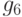 и
и 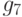 в приведенной диаграмме
следует из предположения о том, что элементы, которые получены редукцией
элементов, следующих за
в приведенной диаграмме
следует из предположения о том, что элементы, которые получены редукцией
элементов, следующих за  , в частности,
, в частности, 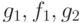 ,
удовлетворяют условию слияния.
,
удовлетворяют условию слияния.
Следующая теорема перечисляет ряд условий, которые равносильны
определению базиса Гребнера. Следует отметить, что среди них
содержатся условия (6') и (7')
и
, позволяющие за конечное число шагов
проверить, является ли выписанная система образующих подмодуля  его базисом Гребнера.
его базисом Гребнера.