|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
9.11. ОПРЕДЕЛЕНИЕ. правильным если из условия 
 следует
следует 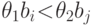 для всех
для всех 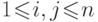 .
.
9.12. ПРИМЕР.
Пусть задан ранжир на множестве мономов  . Будем сравнивать
термы
вида
. Будем сравнивать
термы
вида 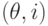 по их последней координате
по их последней координате  и
только в случае равенства ее для двух
термов переходить к сравнению мономов. Полученный таким образом ранжир на
и
только в случае равенства ее для двух
термов переходить к сравнению мономов. Полученный таким образом ранжир на 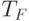 не является правильным.
не является правильным.
9.13. ПРИМЕР.
Пусть 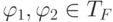 . Будем считать, что
. Будем считать, что 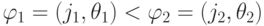 тогда и только тогда,
когда
тогда и только тогда,
когда
- либо
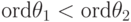 ;
; - либо
 и
и 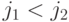 ;
; - либо
 ,
,  и
и 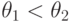 относительно лексикографического порядка при
фиксированной нумерации переменных.
относительно лексикографического порядка при
фиксированной нумерации переменных.
Этот ранжир является правильным. Мы будем называть его стандартным.
Отметим, что по определению ранжира множество термов 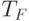 вполне упорядочено относительно каждого ранжира.
вполне упорядочено относительно каждого ранжира.
9.14. ОПРЕДЕЛЕНИЕ.
Пусть задан ранжир на множестве термов 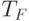 , и пусть
, и пусть 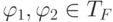 . Будем говорить, что терм
. Будем говорить, что терм 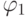 ниже(выше) рангом, чем
ниже(выше) рангом, чем 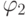 , если
, если 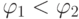
 .
.
Кроме отношения порядка  на
на 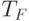 , определим
отношение частичного порядка
, определим
отношение частичного порядка  следующим образом:
следующим образом:
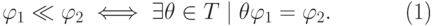 |
( 9.3) |
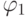 делит
делит 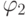 . Из
(1) следует, что < совместно с
. Из
(1) следует, что < совместно с  |
( 9.4) |
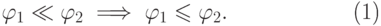
9.15. ОПРЕДЕЛЕНИЕ.
Любой элемент 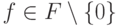 допускает единственное
представление в виде конечной суммы:
допускает единственное
представление в виде конечной суммы:
![f=\smash[b]{\sum_{i=1}^r} c(f,\phi_i )\phi_i,\quad 0 \ne c(f,\phi_i)\in K,\
\phi_i\in T_F,\label{4.1.7}\\
\phi_r<\phi_{r-1}<\dots<\phi_1.\notag](/sites/default/files/tex_cache/93ec6e7e6210f4512fe6a0c7490350a5.png)
 как
как  и старший коэффициент
как
и старший коэффициент
как 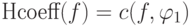 . Определим
. Определим 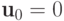 ,
,  . Аналогично,
. Аналогично, 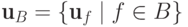 для любого конечного множества
для любого конечного множества 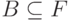 ,
,  для
любого подмодуля
для
любого подмодуля 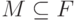 обозначает подмодуль, порожденный
множеством
обозначает подмодуль, порожденный
множеством 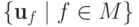 .
.Пусть  - свободный
- свободный  -модуль и
-модуль и 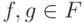 . Будем говорить, что элемент
. Будем говорить, что элемент  ниже
рангом, чем
ниже
рангом, чем  , и писать
, и писать  , если
, если  . Будем говорить, что элемент
. Будем говорить, что элемент  выше рангом,
чем
выше рангом,
чем  , и писать
, и писать 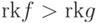 , если
, если  . Если
. Если  , то будем говорить, что элементы
, то будем говорить, что элементы  и
и  имеют одинаковый ранг. Ясно, что различные элементы могут иметь
одинаковый ранг.
имеют одинаковый ранг. Ясно, что различные элементы могут иметь
одинаковый ранг.
9.16. ОПРЕДЕЛЕНИЕ.
Пусть 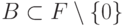 - конечное множество
образующих некоторого
- конечное множество
образующих некоторого  -модуля
-модуля 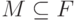 (без
потери общности
можно предположить, что
(без
потери общности
можно предположить, что  для любого
для любого 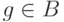 ). Определим процесс редукции
следующим образом:
). Определим процесс редукции
следующим образом: 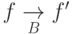 , если
, если 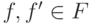 и существуют терм
и существуют терм 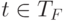 ,
, 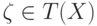 и
и 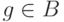 , такие, что
, такие, что  ,
, 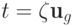 ,
,  .
.
9.17. ЛЕММА.
Пусть 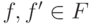 и
и 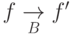 . Тогда
. Тогда 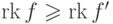 .
.
ДОКАЗАТЕЛЬСТВО.
Утверждение леммы следует из того, что отношение > является
линейным
порядком на множестве термов 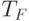 и свойства (2).
и свойства (2).
В дальнейшем будем опускать указание на множество  ,
если это не приведет к двусмысленности или если выбор множества
,
если это не приведет к двусмысленности или если выбор множества  несуществен. Символ
несуществен. Символ 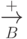 обозначает
транзитивное, а
обозначает
транзитивное, а 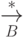 -
рефлексивноранзитивное замыкание отношения
-
рефлексивноранзитивное замыкание отношения 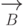 . Элемент
. Элемент  называется нередуцируемым, если не существует элемента
называется нередуцируемым, если не существует элемента 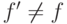 , такого,
что
, такого,
что 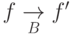 , в противном случае
, в противном случае  называется редуцируемым.
называется редуцируемым.
9.18. ПРИМЕРЫ.
- Пусть
 , т.е.
, т.е.  - векторное пространство над полем
- векторное пространство над полем  .
Рассмотрим стандартный ранжир на
.
Рассмотрим стандартный ранжир на 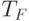 .
Если
.
Если 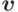 - вектор, у которого первая
ненулевая координата стоит на
- вектор, у которого первая
ненулевая координата стоит на  -м месте, то редукция вектора
-м месте, то редукция вектора 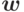 относительно
относительно 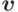 приводит к обнулению
приводит к обнулению  -й координаты вектора
-й координаты вектора 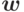 путем вычитания
соответствующего кратного вектора
путем вычитания
соответствующего кратного вектора 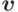 .
. - Пусть
 - поле,
- поле, 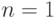 и
и 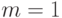 , т.е.
, т.е.  - кольцо многочленов от одной
переменной. Рассмотрим
стандартный ранжир на
- кольцо многочленов от одной
переменной. Рассмотрим
стандартный ранжир на 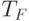 . Пусть
. Пусть 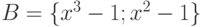 .
Тогда
.
Тогда ![x^4\smash[b]{\underset B\to} x](/sites/default/files/tex_cache/d98b030468f6b91ac300beb4872645ba.png) и
и 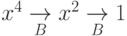 .
.
9.19. ОПРЕДЕЛЕНИЕ.
Пусть на свободном  -модуле
-модуле  дано отношение
редукции
дано отношение
редукции 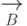 и вычислимая функция
и вычислимая функция 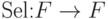 такая, что
такая, что  для любого редуцируемого элемента
для любого редуцируемого элемента  . Рассмотрим вычислимую функцию
. Рассмотрим вычислимую функцию  ,
определяемую рекурсивно
формулой
,
определяемую рекурсивно
формулой

 такого вида назовем нормальной
редукцией
или алгоритмом нормальной
формы для
такого вида назовем нормальной
редукцией
или алгоритмом нормальной
формы для 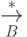 . Например, редуцируемые термы выбираются в порядке
убывания относительно полного упорядочения термов, а при фиксированном терме
соотношения выбираются в том порядке, как они
располагаются в множестве
. Например, редуцируемые термы выбираются в порядке
убывания относительно полного упорядочения термов, а при фиксированном терме
соотношения выбираются в том порядке, как они
располагаются в множестве  .
.9.20. ОПРЕДЕЛЕНИЕ. Частичную редукцию определим как нормальную редукцию, осуществляемую только до тех пор, пока редуцируется лидер.
9.21. ЛЕММА. Если  , то элементы
, то элементы  и
и 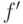 принадлежат одному и тому же смежному классу модуля
принадлежат одному и тому же смежному классу модуля 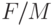 , где
, где  - подмодуль, порожденный множеством
- подмодуль, порожденный множеством  .
.

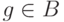 , следовательно,
, следовательно, 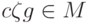 .
.