|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
9.34. УПРАЖНЕНИЕ. Показать, что многочлены
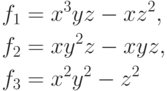
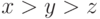 ).
).9.35. УПРАЖНЕНИЕ. Показать, что многочлены
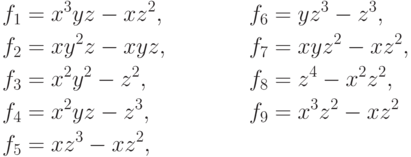
9.36. УПРАЖНЕНИЕ.
Показать, что, используя теорему 9.33.11, в предыдущем упражнении
достаточно рассмотреть  -элементы
для пар (2,3), (2,4), (5,6), (4,7), (2,7), (5,7), (5,8), (6,8), (4,9), (5,9).
-элементы
для пар (2,3), (2,4), (5,6), (4,7), (2,7), (5,7), (5,8), (6,8), (4,9), (5,9).
9.37. УПРАЖНЕНИЕ.
Пусть  - кольцо обобщенных многочленов над полем от конечного
числа неизвестных,
- кольцо обобщенных многочленов над полем от конечного
числа неизвестных,  - свободный
- свободный  -модуль и ранжир
на множестве термов
-модуль и ранжир
на множестве термов 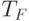 правильный.
Пусть
правильный.
Пусть  - подмодуль модуля
- подмодуль модуля  и
и  - базис Гребнера подмодуля
- базис Гребнера подмодуля  .
Показать, что для каждого элемента
.
Показать, что для каждого элемента 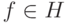 существует представление
существует представление 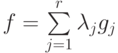 , где
, где 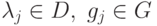 , такое, что
, такое, что 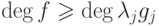 для всех
для всех 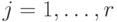 .
.
Если данная система элементов не является базисом Гребнера порождаемого ею
подмодуля, то ее можно расширить, присоединяя
поочередно элементы, получающиеся редуцированием  -элементов.
-элементов.
9.38. УПРАЖНЕНИЕ. Доказать конечность следующего рекурсивного алгоритма построения базиса Гребнера полиномиального идеала (алгоритм пополнения).
Алгоритм  (
( 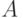 )
)

Очевидно, что сформулированный алгоритм не является оптимальным. Учитывая роль, которую базисы Гребнера играют в компьютерной алгебре, и высокую сложность алгоритмов их построения, оптимизация этих алгоритмов приобретает особое значение. Вопросы оптимизации будут рассмотрены несколько позже.
Базис Гребнера для любого подмодуля  определен неоднозначно.
В частности, после присоединения к базису Гребнера модуля
определен неоднозначно.
В частности, после присоединения к базису Гребнера модуля  любого элемента
любого элемента 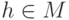 снова получаем базис Гребнера модуля
снова получаем базис Гребнера модуля  . Естественно возникает вопрос о минимальных базисах
Гребнера.
. Естественно возникает вопрос о минимальных базисах
Гребнера.
Следующая терминология пришла из дифференциальной алгебры.
9.39. ОПРЕДЕЛЕНИЕ.
Подмножество 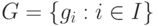 свободного модуля
свободного модуля  называется авторедуцированным множеством, если любой элемент
называется авторедуцированным множеством, если любой элемент 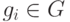 нередуцируем
относительно
нередуцируем
относительно 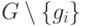 .
.
Из определения немедленно следует, что лидеры всех элементов, принадлежащих авторедуцированному множеству, различны.
9.40. ПРЕДЛОЖЕНИЕ. Пусть  - кольцо обобщенных многочленов от переменных
- кольцо обобщенных многочленов от переменных 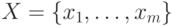 над полем
над полем  и
и  - свободный
- свободный  -модуль с
базисом
-модуль с
базисом 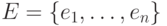 . Любое авторедуцированное множество в
. Любое авторедуцированное множество в  состоит из конечного числа элементов, следовательно, его
элементы можно упорядочить по возрастанию лидеров.
состоит из конечного числа элементов, следовательно, его
элементы можно упорядочить по возрастанию лидеров.
ДОКАЗАТЕЛЬСТВО. Доказательство немедленно следует из леммы 12.1.
Зафиксировав ранжир < на множестве термов 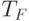 ,
можно ввести отношение частичного порядка на множестве авторедуцированных
множеств.
,
можно ввести отношение частичного порядка на множестве авторедуцированных
множеств.
Пусть 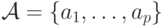 и
и 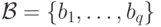 - авторедуцированные множества, элементы которых упорядочены по
возрастанию лидеров. Будем считать, что
- авторедуцированные множества, элементы которых упорядочены по
возрастанию лидеров. Будем считать, что  , если,
, если,
- либо существует
 ,
, 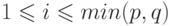 , такое, что
, такое, что  и
и 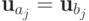 для всех
для всех  ,
, - либо
 и
и 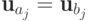 для
для 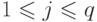 .
.
9.41. ЛЕММА. Любое множество 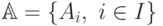 авторедуцированных
подмножеств содержит минимальный элемент относительно введенного
частичного порядка. Минимальный элемент в множестве всех авторедуцированных
подмножеств некоторого подмодуля
авторедуцированных
подмножеств содержит минимальный элемент относительно введенного
частичного порядка. Минимальный элемент в множестве всех авторедуцированных
подмножеств некоторого подмодуля  свободного
свободного  -модуля является базисом Гребнера модуля
-модуля является базисом Гребнера модуля  .
.
ДОКАЗАТЕЛЬСТВО.
По предложению 9.40 мы можем
предполагать, что элементы в наших авторедуцированных множествах упорядочены по
возрастанию старших термов. Зафиксируем минимальное значение лидера для первых
элементов рассматриваемых авторедуцированных
множеств (это значение определено однозначно, поскольку множество термов
вполне упорядочено). Обозначим этот лидер 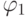 .
В системе авторедуцированных множеств
.
В системе авторедуцированных множеств 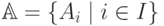 рассмотрим подсистему
рассмотрим подсистему 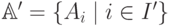 множеств
множеств 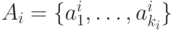 , таких, что
, таких, что  . В
. В 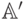 найдем минимальное
значение лидера вторых
элементов, обозначим его
найдем минимальное
значение лидера вторых
элементов, обозначим его 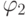 . Продолжая подобным образом,
получим авторедуцированную систему термов, упорядоченную по
возрастанию ранга их лидеров. По предложению 9.40 эта система должна обрываться на конечном
шаге. Выбор системы
лидеров осуществлялся таким образом, чтобы всегда существовало
авторедуцированное множество, лидеры элементов которого имели вид
. Продолжая подобным образом,
получим авторедуцированную систему термов, упорядоченную по
возрастанию ранга их лидеров. По предложению 9.40 эта система должна обрываться на конечном
шаге. Выбор системы
лидеров осуществлялся таким образом, чтобы всегда существовало
авторедуцированное множество, лидеры элементов которого имели вид 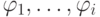 . Авторедуцированное множество,
соответствующее полной системе
. Авторедуцированное множество,
соответствующее полной системе 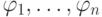 , является
минимальным.
, является
минимальным.
Для доказательства того, что  - базис Гребнера модуля
- базис Гребнера модуля  , воспользуемся условием 2 теоремы 9.33
Предположим противное, тогда существует элемент
, воспользуемся условием 2 теоремы 9.33
Предположим противное, тогда существует элемент 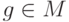 , старший
терм
, старший
терм  которого редуцирован относительно
которого редуцирован относительно 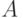 . Можно
предполагать, что он сам также редуцирован относительно
. Можно
предполагать, что он сам также редуцирован относительно 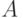 .
Рассмотрим множество
.
Рассмотрим множество
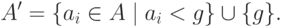
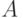 , что
противоречит предположению о минимальности
, что
противоречит предположению о минимальности 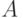 .
.9.42. СЛЕДСТВИЕ. Пусть  - кольцо обобщенных многочленов над полем,
- кольцо обобщенных многочленов над полем,  - свободный конечнопорожденный
- свободный конечнопорожденный  -модуль.
Тогда для каждого
подмодуля
-модуль.
Тогда для каждого
подмодуля  модуля
модуля  существует базис Гребнера.
существует базис Гребнера.
9.43. СЛЕДСТВИЕ. Всякое кольцо обобщенных многочленов над полем является (слева) нетеровым.
ДОКАЗАТЕЛЬСТВО. Как следует из следствия 9.42, во всяком левом идеале такого кольца существует базис Гребнера. Как видно из определения 9.26, базис Гребнера конечен и порождает этот идеал.
9.44. ОПРЕДЕЛЕНИЕ.
Базис Гребнера  модуля
модуля 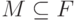 назовем
авторедуцированным, если
множество
назовем
авторедуцированным, если
множество  авторедуцировано.
авторедуцировано.
9.45. ПРЕДЛОЖЕНИЕ.
Авторедуцированный базис Гребнера модуля  определен однозначно с
точностью до умножения его элементов на константы из поля
определен однозначно с
точностью до умножения его элементов на константы из поля  .
.
ДОКАЗАТЕЛЬСТВО.
Среди всех авторедуцированных подмножеств модуля  выберем
минимальное. Обозначим его
выберем
минимальное. Обозначим его 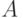 и предположим, что его элементы
нормированы так, что все их старшие коэффициенты равны 1. Покажем, что этим
условием множество
и предположим, что его элементы
нормированы так, что все их старшие коэффициенты равны 1. Покажем, что этим
условием множество 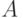 определено однозначно и что
оно является базисом Гребнера модуля
определено однозначно и что
оно является базисом Гребнера модуля  .
.
Предположим, что 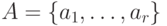 и
и 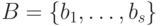 -
два множества, удовлетворяющих сформулированным выше условиям.
Из условия минимальности следует, что
-
два множества, удовлетворяющих сформулированным выше условиям.
Из условия минимальности следует, что 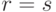 и
и  для любого
для любого  . Предположим, что существует
. Предположим, что существует  ,
для которого
,
для которого 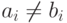 . Ненулевой элемент
. Ненулевой элемент 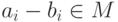 редуцирован относительно
редуцирован относительно 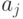 для
для  ,
поскольку нередуцируемость зависит только от множеств лидеров для
,
поскольку нередуцируемость зависит только от множеств лидеров для 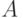 и
и 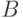 ,
а эти множества лидеров совпадают. По лемме 9.41
,
а эти множества лидеров совпадают. По лемме 9.41 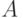 - базис Гребнера
модуля
- базис Гребнера
модуля  ,
что противоречит нетривиальности элемента
,
что противоречит нетривиальности элемента  .
.
9.46. ОПРЕДЕЛЕНИЕ.
Пусть 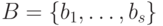 -
-  -базис модуля
-базис модуля 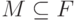 , относительно некоторого упорядочения термов из
, относительно некоторого упорядочения термов из 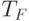 . Назовем
базис
. Назовем
базис 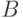 редуцируемым, если
для некоторого
редуцируемым, если
для некоторого  ,
, 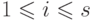 , существует
, существует  -представление
-представление ![b_i = \smash[b]{\sum\limits_{j\neq i}} c_j
b_j](/sites/default/files/tex_cache/3dbc4225152d2956628ed92ea1e64f53.png) , в противном случае
, в противном случае 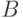 называем нередуцируемым.
называем нередуцируемым.
9.47. ОПРЕДЕЛЕНИЕ.  -базис
-базис 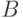 модуля
модуля  , содержащий
, содержащий  элементов, назовем минимальным, если не
существует
элементов, назовем минимальным, если не
существует  -базиса
-базиса 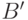 модуля
модуля  ,
содержащего менее
,
содержащего менее  элементов.
элементов.
9.48. ПРЕДЛОЖЕНИЕ. Понятия минимальности и нередуцируемости  -базисов совпадают.
Каждый авторедуцированный
-базисов совпадают.
Каждый авторедуцированный  -базис минимален, и каждый минимальный
-базис минимален, и каждый минимальный  -базис квазиавторедуцирован, т.е. множество его лидеров
авторедуцировано (это множество определяется модулем
-базис квазиавторедуцирован, т.е. множество его лидеров
авторедуцировано (это множество определяется модулем  однозначно).
однозначно).
ДОКАЗАТЕЛЬСТВО.
Очевидно, что редуцируемый  -базис не является минимальным. Таким
образом для доказательства предложения достаточно показать,
что лидеры элементов нередуцируемого базиса определены однозначно.
Доказательство проходит во многом аналогично доказательству
предложения 9.45 и оставляется
читателю в качестве самостоятельного упражнения.
-базис не является минимальным. Таким
образом для доказательства предложения достаточно показать,
что лидеры элементов нередуцируемого базиса определены однозначно.
Доказательство проходит во многом аналогично доказательству
предложения 9.45 и оставляется
читателю в качестве самостоятельного упражнения.
9.49. ПРИМЕРЫ.
- Пусть
 - поле и
- поле и  .
Если матрица системы линейных многочленов приведена к ступенчатому виду, т.е.
нет строк, которые
начинаются с одного и того же столбца, то эта система представляет собой
базис Гребнера порождаемого ею модуля. Показать,
что обратное, в общем случае, неверно, т.е. могут существовать базисы
Гребнера векторного подпространства, первые ненулевые
элементы различных векторов которых стоят в одном и том же столбце.
.
Если матрица системы линейных многочленов приведена к ступенчатому виду, т.е.
нет строк, которые
начинаются с одного и того же столбца, то эта система представляет собой
базис Гребнера порождаемого ею модуля. Показать,
что обратное, в общем случае, неверно, т.е. могут существовать базисы
Гребнера векторного подпространства, первые ненулевые
элементы различных векторов которых стоят в одном и том же столбце. - Пусть
 - поле,
- поле,  . Множество
. Множество 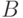 является базисом Гребнера порождаемого им идеала тогда и
только тогда, когда оно
содержит НОД всех своих элементов. Минимальный базис Гребнера в этом
случае состоит из одного элемента.
является базисом Гребнера порождаемого им идеала тогда и
только тогда, когда оно
содержит НОД всех своих элементов. Минимальный базис Гребнера в этом
случае состоит из одного элемента. - Базис Гребнера в упражнении 9.35 не является минимальным. После удаления из него первого элемента он становится минимальным и даже авторедуцированным.
9.50. УПРАЖНЕНИЕ. Показать, что система алгебраических уравнений не имеет решений в алгебраическом замыкании поля коэффициентов тогда и только тогда, когда базис Гребнера идеала, порожденного этой системой, содержит константу.
9.51. УПРАЖНЕНИЕ.
Показать, что система алгебраических уравнений из ![K[x_1,\dots,x_n
]](/sites/default/files/tex_cache/f41ee29e640db5a3fc71e3d3d8715603.png) имеет конечное множество решений в алгебраическом
замыкании поля коэффициентов тогда и только тогда, когда базис Гребнера
идеала, порожденного этой системой, содержит для любого
имеет конечное множество решений в алгебраическом
замыкании поля коэффициентов тогда и только тогда, когда базис Гребнера
идеала, порожденного этой системой, содержит для любого 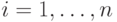 многочлен со старшим мономом, являющимся степенью
многочлен со старшим мономом, являющимся степенью  .
.
9.52. УПРАЖНЕНИЕ.
Построить теорию базисов Гребнера для идеалов в кольце многочленов с
коэффициентами из кольца  .
.
