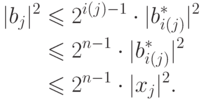|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Редуцированные базисы решетки. Редуцирование базиса в решетке
Редуцированные базисы решетки
19.1. ОПРЕДЕЛЕНИЕ. Решеткой в  -мерном векторном пространстве над полем
вещественных чисел
-мерном векторном пространстве над полем
вещественных чисел  или над полем рациональных чисел
или над полем рациональных чисел  называется
свободный
называется
свободный 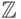 -модуль
-модуль  ранга
ранга  , т.е.
существует базис
, т.е.
существует базис 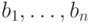 пространства
пространства 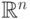 (соответственно
(соответственно 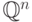 ), такой, что
), такой, что
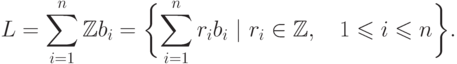
 называется рангом решетки, а множество векторов
называется рангом решетки, а множество векторов 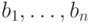 - ее базисом.
- ее базисом.19.2. ОПРЕДЕЛЕНИЕ. Детерминантом 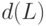 решетки
решетки  называется положительное число,
определяемое формулой
называется положительное число,
определяемое формулой
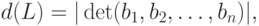
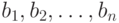 решетки
решетки  .
.19.3. УПРАЖНЕНИЕ.
Показать, что определение 19.2
является корректным,
т.е. 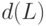 не зависит от выбора базиса решетки
не зависит от выбора базиса решетки  .
.
Прежде чем дать определение редуцированного базиса решетки, нам
необходимо
напомнить процесс ортогонализации Грама-Шмидта.
Векторы 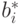
 и вещественные числа
и вещественные числа 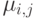
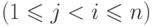 определяются по индукции
формулами
определяются по индукции
формулами
 |
( 19.1) |
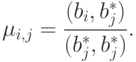 |
( 19.2) |
Отметим, что 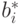 - проекция вектора
- проекция вектора 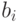 на ортогональное дополнение
к пространству
на ортогональное дополнение
к пространству 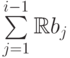 в пространстве
в пространстве 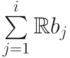 и что
и что ![\sum\limits\limits _{j=1}^i \mathbb R b_j = \smash[t]{\sum\limits\limits
_{j=1}^i} \mathbb R b_j^*](/sites/default/files/tex_cache/48f8ab38a71c60be80a9fe0486e6ec57.png) для
для 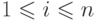 .
Таким образом векторы
.
Таким образом векторы 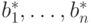 образуют
ортогональный базис
пространства
образуют
ортогональный базис
пространства 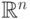 .
.
В дальнейшем символ 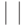 используется как для обозначения
абсолютной
величины вещественных или комплексных чисел, так и для обозначения евклидовой
длины вектора в вещественном векторном пространстве.
используется как для обозначения
абсолютной
величины вещественных или комплексных чисел, так и для обозначения евклидовой
длины вектора в вещественном векторном пространстве.
19.4. УПРАЖНЕНИЕ. Показать, что


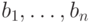 решетки
решетки  выполняется неравенство Адамара
выполняется неравенство Адамара 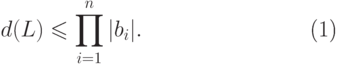 |
( 19.3) |
19.6. ОПРЕДЕЛЕНИЕ.
Базис 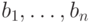 решетки
решетки  называется редуцированным редуцированным, если выполняются неравенства
называется редуцированным редуцированным, если выполняются неравенства
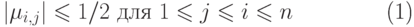 |
( 19.4) |
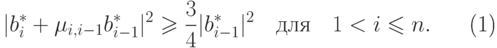 |
( 19.5) |
Векторы 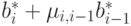 и
и 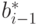 имеют простой
геометрический смысл - это проекции векторов
имеют простой
геометрический смысл - это проекции векторов 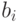 и
и 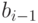 на
ортогональное дополнение к пространству
на
ортогональное дополнение к пространству 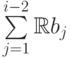 в
в 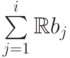 . Константа 3/4 выбирается в
значительной мере
произвольно: вместо нее можно взять любое фиксированное вещественное число
. Константа 3/4 выбирается в
значительной мере
произвольно: вместо нее можно взять любое фиксированное вещественное число  , удовлетворяющее условию
, удовлетворяющее условию  .
.
Грубо говоря, редуцированный базис состоит из "почти ортогональных" векторов, расположенных в порядке "почти неубывания длин".
Использование редуцированных базисов решеток для целей факторизации
многочленов основано на следующем свойстве таких базисов:
если 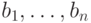 - редуцированный базис решетки
- редуцированный базис решетки  , то
, то
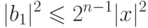
 . К доказательству этого свойства и его
обобщений мы сейчас и переходим.
. К доказательству этого свойства и его
обобщений мы сейчас и переходим.19.7. ПРЕДЛОЖЕНИЕ. Пусть 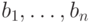 - редуцированный базис решетки
- редуцированный базис решетки  в
в 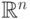 и
векторы
и
векторы 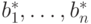 получены из этого базиса процессом
ортогонализации Грама - Шмидта. Тогда
получены из этого базиса процессом
ортогонализации Грама - Шмидта. Тогда
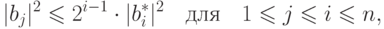 |
( 19.6) |
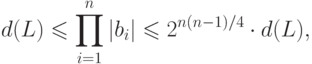 |
( 19.7) |
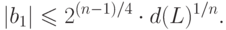 |
( 19.8) |
ДОКАЗАТЕЛЬСТВО. Сначала докажем формулу (19.6). Из формул (19.4) и (19.5) получаем
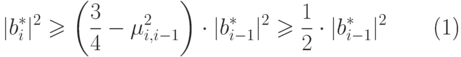 |
( 19.9) |
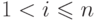 , откуда по индукции выводится неравенство
, откуда по индукции выводится неравенство
Из этих формул следует, что
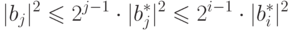
 . Таким образом, формула (19.6)
доказана.
. Таким образом, формула (19.6)
доказана.Для доказательства формулы (19.7) достаточно воспользоваться упражнением 19.4 и неравенствами
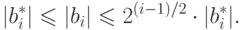
 в формуле (19.6) и перемножив левые и правые части этой формулы для
в формуле (19.6) и перемножив левые и правые части этой формулы для  от 1 до
от 1 до  ,
получим неравенство (19.8). Этим
заканчивается доказательство предложения
19.7.
,
получим неравенство (19.8). Этим
заканчивается доказательство предложения
19.7.19.8. УПРАЖНЕНИЕ.
Показать, что если в формуле (19.5) заменить 3/4 на некоторое
вещественное число  ,
, 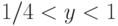 , то появляющиеся в
формулах
(19.6), (19.7) и (19.8) степени числа 2 заменятся на
такие же степени числа
, то появляющиеся в
формулах
(19.6), (19.7) и (19.8) степени числа 2 заменятся на
такие же степени числа 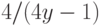 .
.
19.9. ПРЕДЛОЖЕНИЕ. Пусть 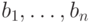 - редуцированный базис решетки
- редуцированный базис решетки  . Тогда для любого ненулевого вектора
. Тогда для любого ненулевого вектора  выполняется неравенство
выполняется неравенство
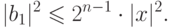
ДОКАЗАТЕЛЬСТВО.
Любой вектор  может быть выражен через векторы базиса
может быть выражен через векторы базиса 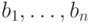 с целыми коэффициентами
с целыми коэффициентами 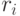 , а через векторы
, а через векторы 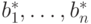 -
в виде линейной комбинации с вещественными коэффициентами
-
в виде линейной комбинации с вещественными коэффициентами 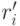 , т.е.
, т.е.
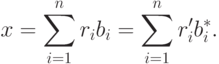
 - наибольший индекс, для которого
- наибольший индекс, для которого  ,
то
,
то 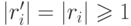 . Таким образом,
. Таким образом,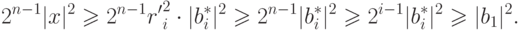
Последние два неравенства вытекают из формулы (19.6).
Обобщением полученного результата является следующее
19.10. ПРЕДЛОЖЕНИЕ. Пусть 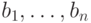 - редуцированный базис решетки
- редуцированный базис решетки  ,
, 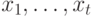 - линейно независимые
векторы решетки
- линейно независимые
векторы решетки  . Тогда для
любого
. Тогда для
любого  от 1 до
от 1 до  выполняется неравенство
выполняется неравенство
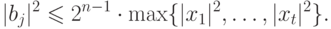
ДОКАЗАТЕЛЬСТВО.
Выразим векторы 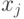 через элементы базиса
через элементы базиса 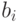 :
:
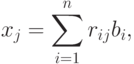

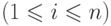 для
для 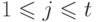 . Для каждого фиксированного
. Для каждого фиксированного  через
через 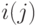 обозначим наибольшее
значение
обозначим наибольшее
значение  , для которого
, для которого  . Перенумеруем
векторы
. Перенумеруем
векторы 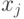 так,
чтобы числа
так,
чтобы числа 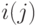 не убывали, т.е.
не убывали, т.е. 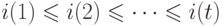 . Из
доказательства предыдущего предложения можно получить неравенство
. Из
доказательства предыдущего предложения можно получить неравенство |
( 19.10) |
Покажем, что 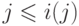 для всех
для всех  от 1 до
от 1 до  . Если это неравенство
для некоторого
. Если это неравенство
для некоторого  не выполняется, то все векторы
не выполняется, то все векторы 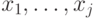 принадлежат
подпространству
принадлежат
подпространству 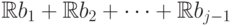 , что
противоречит линейной
независимости векторов
, что
противоречит линейной
независимости векторов 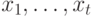 . Воспользовавшись
неравенством
. Воспользовавшись
неравенством 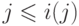 и формулами (19.6) и (19.10), получаем для всех
и формулами (19.6) и (19.10), получаем для всех  от 1 до
от 1 до  неравенство
неравенство