|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Разложение многочленов на неприводимые множители по модулю p. Лемма Гензеля
Разложение многочленов на неприводимые множители по модулю p
Этот раздел посвящен детализации предписания "нулевое приближение разложения". Разделим его на два этапа:
- разложить многочлен на неприводимые множители по
модулю простого
 ;
; - найти добавочные множители
 .
.
Результатом первого этапа будет целое  и вектор
и вектор  элементов типа многочлен с индексом
элементов типа многочлен с индексом  .
.
Результатом второго этапа должен явиться вектор  элементов
типа
элементов
типа ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) с индексом
с индексом  , такой, что
, такой, что
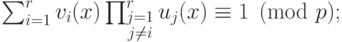
 накладываются условия
накладываются условия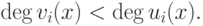
 понадобится нам в предписании "выполнить шаг
итерации".
понадобится нам в предписании "выполнить шаг
итерации".Второй этап не представляет принципиальной трудности. Для его выполнения достаточно разложить рациональную функцию на элементарные дроби, что можно сделать методом неопределенных коэффициентов

Как и в случае простых чисел, задача разложения многочлена на простые
множители безусловно
сложнее, чем нахождение НОД, но если выполнять
разложение по модулю некоторого простого числа,
то оно осуществляется не так сложно, как можно
было бы ожидать. Значительно проще найти простые
множители произвольного многочлена степени  по
модулю 2, чем с помощью любого из известных методов определить
сомножители произвольного
по
модулю 2, чем с помощью любого из известных методов определить
сомножители произвольного  -разрядного числа в двоичной системе счисления.
Этот удивительный факт — следствие алгоритма
разложения, открытого в 1967 году Элвином Р. Берлекэмпом.
-разрядного числа в двоичной системе счисления.
Этот удивительный факт — следствие алгоритма
разложения, открытого в 1967 году Элвином Р. Берлекэмпом.
Основными результатами, на которых основан алгоритм Берлекэмпа, является малая теорема Ферма и китайская теорема об остатках.
17.1. ТЕОРЕМА (Ферма малая). Если  - простое число, то для любого
- простое число, то для любого 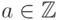 выполняется сравнение
выполняется сравнение 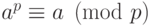 .
.
17.2. ЗАМЕЧАНИЕ.
Малая теорема Ферма может использоваться в алгоритмах проверки простоты
натуральных чисел, а именно, если 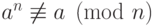 для некоторого
для некоторого 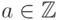 , то
, то  - составное число.
Существуют однако составные числа
- составное число.
Существуют однако составные числа  , для которых
, для которых 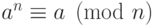 для
любого
для
любого 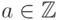 .
.
17.3. ОПРЕДЕЛЕНИЕ.
Составное число  , такое, что сравнение
, такое, что сравнение 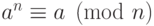 выполняется для любого
выполняется для любого 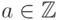 , называется кармайкловым.
, называется кармайкловым.
17.4. УПРАЖНЕНИЕ. Найти несколько первых кармайкловых чисел.
17.5. ТЕОРЕМА (китайская об остатках для целых чисел). Пусть 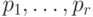 - попарно взаимно простые целые
числа. Для любого набора
- попарно взаимно простые целые
числа. Для любого набора  целых чисел существует
целое
число
целых чисел существует
целое
число  , такое, что
, такое, что 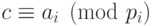 для любого
для любого 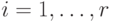 . Условием
. Условием ![0\le
c<\smash[b]{\prod\limits_{i=1}^r} p_i](/sites/default/files/tex_cache/503ac0a6f595965193264fad0509e9a7.png) число
число  определяется
однозначно.
определяется
однозначно.
17.6. ТЕОРЕМА (китайская об остатках для многочленов). Пусть  - поле и
- поле и 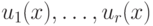 - попарно взаимно простые многочлены из
- попарно взаимно простые многочлены из ![k[x]](/sites/default/files/tex_cache/d2dc614757f6915915ec0ba146b72528.png) . Для любого набора
. Для любого набора 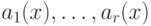 многочленов из
многочленов из ![k[x]](/sites/default/files/tex_cache/d2dc614757f6915915ec0ba146b72528.png) существует
многочлен
существует
многочлен 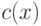 , такой, что
, такой, что 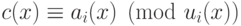 для
любого
для
любого 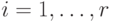 . Условием
. Условием ![\deg c(x)<\smash[b]{\sum\limits_{i=1}^r} \deg u_i(x)](/sites/default/files/tex_cache/9ccdd38234834ad99c588f90cd3b022d.png) многочлен
многочлен 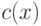 определяется однозначно.
определяется однозначно.
17.7. СЛЕДСТВИЕ.
Пусть  - простое число,
- простое число, 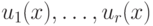 - попарно взаимно простые многочлены из
- попарно взаимно простые многочлены из ![F_p[x]](/sites/default/files/tex_cache/08046df968872bddd17f9de3e18ba88a.png) . Для любого
набора
. Для любого
набора 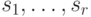 целых чисел существует единственный многочлен
целых чисел существует единственный многочлен  , такой, что
, такой, что
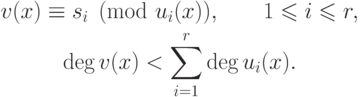 |
( 17.1) |
Доказательства малой теоремы Ферма и китайской теоремы об остатках могут быть найдены в большинстве учебников по алгебре и теории чисел и оставляются читателю в качестве упражнения.
Пусть  - простое число. Все рассматриваемые ниже
операции с многочленами будут выполняться по модулю
- простое число. Все рассматриваемые ниже
операции с многочленами будут выполняться по модулю  .
.
Предположим, что задан многочлен 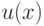 , коэффициенты которoго
выбраны из множества
, коэффициенты которoго
выбраны из множества 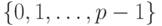 . Считаем, что многочлен
. Считаем, что многочлен 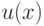 нормирован,
т.e его старший коэффициент равен 1 и
свободен от квадратов, если его рассматривать
над полем
нормирован,
т.e его старший коэффициент равен 1 и
свободен от квадратов, если его рассматривать
над полем 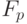 . Если это условие не выполнено, то
можно воспользоваться результатом задачи 15.1.
. Если это условие не выполнено, то
можно воспользоваться результатом задачи 15.1.
17.8. ПРЕДЛОЖЕНИЕ. Для любого многочлена ![v(x)\in F_p[x]](/sites/default/files/tex_cache/137e9f95c16df054c3b042dfabd0e212.png)
![\begin{equation*}
v(x^p) =[v(x)]^p.
\end{equation*}](/sites/default/files/tex_cache/f2f41793f203b921248b7af60821cf2b.png) |
( 17.2) |
ДОКАЗАТЕЛЬСТВО.
Для любых многочленов 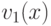 и
и ![v_2(x)\in\mathbb Z[x]](/sites/default/files/tex_cache/c395605a6d18a2a55051c13084f882fd.png) по
модулю
по
модулю  выполняются равенства
выполняются равенства
![\begin{align*}
(v_1(x)\cdot v_2(x))^p&= (v_1(x))^p\cdot (v_2(x))^p ,\\
[v_1(x)+v_2(x)]^p&=v_1^p+ C_p^1v_1^{p-1}v_2+\dots+ v_2^p
=v_1^p(x)+v_2^p(x),
\end{align*}](/sites/default/files/tex_cache/3cfe3691d9fcd4a418f433d8da508eb1.png)
 (т.е. в
(т.е. в 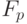 обращаются в нуль). Далее, для всякого целого числа
обращаются в нуль). Далее, для всякого целого числа  по малой теореме Ферма имеем
по малой теореме Ферма имеем  . Поэтому, если
. Поэтому, если 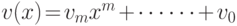 , то
, то![\begin{align*}
[v(x)]^p=(v_mx^m)^p+\dots+ (v_0)^p
=v_mx^{mp}+\dots+ v_1x^p+v_0= v(x^p),
\end{align*}](/sites/default/files/tex_cache/f8dbedcaa6d964e2d8f6b6154af3279e.png)
Идея Берлекэмпа состоит в том, чтобы для нахождения неприводимых
сомножителей 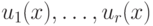 многочлена
многочлена ![f(x)\in
F_p[x]](/sites/default/files/tex_cache/190f8d48378fcd559826f55cfde3e59e.png) воспользоваться теперь китайской теоремой об остатках для многочленов, точнее,
следствием 17.7.
(Отметим, что сравнение выполняется в кольце
многочленов с коэффициентами из конечного поля,
т.е. утверждение
воспользоваться теперь китайской теоремой об остатках для многочленов, точнее,
следствием 17.7.
(Отметим, что сравнение выполняется в кольце
многочленов с коэффициентами из конечного поля,
т.е. утверждение  означает, что разность
означает, что разность  в кольце
в кольце ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) принадлежит идеалу, порожденному элементами
принадлежит идеалу, порожденному элементами 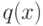 и
и  .)
.)
Если нам известен многочлен  , удовлетворяющий системе
сравнений ( 17.1 ), то можно
получить разложение
, удовлетворяющий системе
сравнений ( 17.1 ), то можно
получить разложение  на
множители,
используя тот факт, что если
на
множители,
используя тот факт, что если 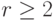 и
и 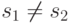 ,
то
,
то 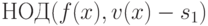 делится на
делится на 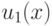 и
не делится на
и
не делится на 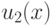 .}
.}
Поскольку решение системы (17.1) может оказаться полезным для
решения интересующей нас задачи разложения многочлена на
множители, рассмотрим систему (17.1) более подробно. Прежде всего
заметим, что решение  этой системы удовлетворяет
условию
этой системы удовлетворяет
условию

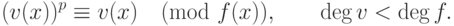 |
( 17.3) |
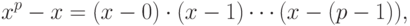
 удовлетворяет соотношению
удовлетворяет соотношению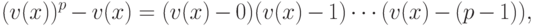 |
( 17.4) |
 .
Отсюда следует, что если многочлен
.
Отсюда следует, что если многочлен  удовлетворяет соотношению
(17.3), то
удовлетворяет соотношению
(17.3), то  делит левую
часть \vad равенства (17.4), а следовательно, любой
неприводимый множитель многочлена
делит левую
часть \vad равенства (17.4), а следовательно, любой
неприводимый множитель многочлена  должен
делить один из
должен
делить один из  взаимно простых множителей в
правой части равенства (17.4). Значит, все решения сравнения
(17.3) должны представляться в виде
(17.1) при некотором выборе значений
взаимно простых множителей в
правой части равенства (17.4). Значит, все решения сравнения
(17.3) должны представляться в виде
(17.1) при некотором выборе значений 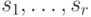 ,
т.е. у этого сравнения имеется ровно
,
т.е. у этого сравнения имеется ровно 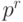 решений.
Таким образом, решения сравнения (17.3) дают нам
ключ к отысканию разложения многочлена
решений.
Таким образом, решения сравнения (17.3) дают нам
ключ к отысканию разложения многочлена  на
неприводимые множители. Может показаться, что
найти все решения сравнения (17.3) еще труднее,
чем разложить
на
неприводимые множители. Может показаться, что
найти все решения сравнения (17.3) еще труднее,
чем разложить  на неприводимые множители,
однако в действительности это не так, поскольку
множество решений сравнений (17.3) замкнуто относительно сложения,
следовательно, оно является
векторным пространством над полем
на неприводимые множители,
однако в действительности это не так, поскольку
множество решений сравнений (17.3) замкнуто относительно сложения,
следовательно, оно является
векторным пространством над полем 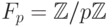 .
.Пусть 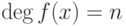 ; рассмотрим матрицу размера
; рассмотрим матрицу размера 
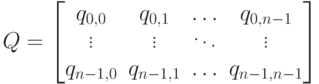
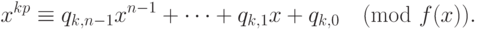
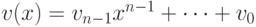 является решением
сравнения (17.3) тогда и только тогда, когда выполняется
векторное равенство
является решением
сравнения (17.3) тогда и только тогда, когда выполняется
векторное равенство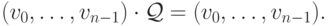
В самом деле, последнее равенство выполняется тогда и только тогда, когда
![v(x)=\sum_j\kern-1pt v_jx^j =\sum_j\sum_k\kern-1pt v_kq_{k,j}x^j\equiv
\sum_k\kern-1pt v_kx^{kp} = v(x^p)\equiv [v(x)]^p\kern-1pt\pmod{\kern-2pt
f(x)}.](/sites/default/files/tex_cache/0574d830961fda93ee5000f4a4ce04a3.png)
Построение матрицы 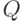 легко можно осуществить следующим
образом. Для сравнительно малых
легко можно осуществить следующим
образом. Для сравнительно малых  можно воспользоваться таким методом вычисления многочленов
можно воспользоваться таким методом вычисления многочленов  . Пусть
. Пусть
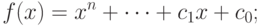
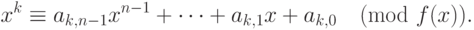
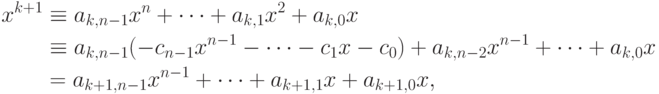
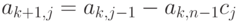 . По определению полагаем
. По определению полагаем 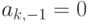 , так что
, так что 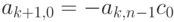 .
Таким образом, алгоритм Берлекэмпа разложения
многочлена на неприводимые множители состоит в
следующем.
.
Таким образом, алгоритм Берлекэмпа разложения
многочлена на неприводимые множители состоит в
следующем.