|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Разложение многочленов на неприводимые множители по модулю p. Лемма Гензеля
А31. АЛГОРИТМ (линейного подъема для нескольких множителей).
$, $\tilde g[i](x)\in \mathbb Z[x]$
$i=1..r$,}\\
\text{ \qquad $p \in \mathbb Z$ - простое число,} \\
\text{\qquad $f(x)\equiv \prod\limits_ig_1[i](x) \pmod p$, }\\
\text{\qquad $1\equiv \sum\limits_i\prod\limits_{j\ne
i}g_1[j](x)\tilde g[i](x) \pmod p$, $k\in \N$} \\
\text{Надо: \qquad $g[i]$ такие, что $f(x)\equiv \prod\limits_ig[i](x) \pmod{p^k}$ }\\
\text{Начало}\\
\text{цикл для $i$ от $1$ до $r$}\\
\text{\qquad $g[i]:=g_1[i]$}\\
\text{конец цикла}\\
\text{цикл для $t$ от $1$ до $k-1$}\\
\text{\qquad $d:=\dfrac{f-\prod\limits_ig[i]}{p^t} \pmod p$}\\
\text{\qquad цикл для $i$ от $1$ до $r$}\\
\text{\qquad \qquad $g_c:= d\cdot \tilde g[i] \pmod{p, g_1[i]}$}\\
\text{\qquad \qquad $g[i]:=g[i]+g_c\cdot p^t$}\\
\text{\qquad конец цикла}\\
\text{конец цикла}\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/480ecba64b517f4efeb44b328f7ab2e0.png)
Изложим теперь вариант леммы Гензеля, основанный на квадратичном подъеме,
т.е. на переходе от сравнения по модулю  к сравнению по
модулю
к сравнению по
модулю 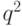 .
Основное его отличие от линейного заключается в том, что сравнение
.
Основное его отличие от линейного заключается в том, что сравнение \tilde g[i](x) \pmod p](/sites/default/files/tex_cache/983b4f57487645117b526e0b73180047.png) ,
заменяется аналогичным
сравнением по переменному модулю
,
заменяется аналогичным
сравнением по переменному модулю  . Естественно, что такое
сравнение
недостаточно выполнить один раз, необходимо вычислять его в основном цикле,
что существенно повышает сложность этого цикла.
. Естественно, что такое
сравнение
недостаточно выполнить один раз, необходимо вычислять его в основном цикле,
что существенно повышает сложность этого цикла.
Рассмотрим задачу в следующей постановке.
-
Дано: полином
![f(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/8049b0ca71684c4e56d841d8cdedce16.png) , число
, число  взаимно простое с
взаимно простое с 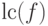 ,
разложение полинома
,
разложение полинома  на взаимно простые множители
над кольцом
вычетов по модулю
на взаимно простые множители
над кольцом
вычетов по модулю  :Предполагается, что
:Предполагается, что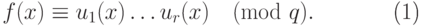
( 18.2) 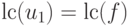 , а старшие
коэффициенты
всех остальных множителей равны 1. Кроме того, заданы значения
переменных
, а старшие
коэффициенты
всех остальных множителей равны 1. Кроме того, заданы значения
переменных 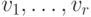 типа полином,
удовлетворяющие условиям:и
типа полином,
удовлетворяющие условиям:и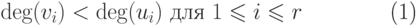
( 18.3) где
( 18.4) 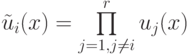 .
Выше сказано, как найти полиномы
.
Выше сказано, как найти полиномы 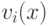 для первого шага
алгоритма (когда
для первого шага
алгоритма (когда  является простым числом). Надо поднять это
разложение до сравнения по модулю
является простым числом). Надо поднять это
разложение до сравнения по модулю 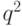 , т.е. найти такие
, т.е. найти такие  , что
, что  ,
старшие коэффициенты всех остальных множителей равны 1, и
,
старшие коэффициенты всех остальных множителей равны 1, и 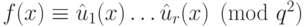 . Требуется также найти
новые
значения переменных
. Требуется также найти
новые
значения переменных 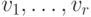 , удовлетворяющие
соотношениям (18.3)
и (18.4), в которых полиномы
, удовлетворяющие
соотношениям (18.3)
и (18.4), в которых полиномы 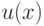 заменены на
заменены на 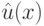 , а
, а  заменено на
заменено на 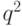 .
.
В рассматриваемом алгоритме факторизации  является степенью
является степенью  , а
множители
, а
множители  получаются подъемом неприводимых
делителей
получаются подъемом неприводимых
делителей  по
модулю
по
модулю  .
.
А32. АЛГОРИТМ (квадратичный подъем 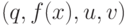 ).
).
![\begin{equation}\\
\text{Дано:\quad $f(x)\in \mathbb Z[x]$} \\
\text{\qquad $q\in \mathbb Z$\qquad\qquad // основание сравнения }\\
\text{\qquad $u,v$ - векторы типа $\mathbb Z[x]$ с
индексом $1..r$}\\
\text{Надо: \qquad $q$ \qquad // новое значение основания сравнения} \\
\text{\qquad $u,v$ \qquad новые значения векторов}\\
\text{Переменные:\quad $t(x)\in \mathbb Z[x]$} \\
\text{\qquad $w$ - вектор элементов типа
$\mathbb Z[x]$ с индексом $1..r$}\\
\text{Начало}\\
\text{$t(x) := (f(x) - \prod\limits_{i=1}^r u_i (x)) \pmod{q^2}$}\\
\text{$t(x) := t(x)/q$}\\
\text{цикл для $i$ от $1$ до $r$}\\
\text{\qquad $w_i(x) :=$ остаток от деления $t(x)\cdot v_i(x) $
на $u_i(x)$ по $\pmod q$}\\
\text{\qquad $u_i(x) := u_i(x) + q\cdot w_i(x)$}\\
\text{конец цикла }\\
\text{$t(x) := (1 - \sum\limits_{i=1}^r v_i(x) \tilde u_i(x))
\pmod{q^2}$}\\
\text{$t (x) := t(x)/q$}\\
\text{цикл для $i$ от $1$ до $r$}\\
\text{\qquad $w_i(x) :=$ остаток от деления $t(x)\cdot v_i(x)$
на $u_i(x)$ по $\pmod q$}\\
\text{\qquad $v_i(x) := v_i(x) + q\cdot w_i(x)$}\\
\text{конец цикла}\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/262235c59bb9cad1ff06a07af41a6d8d.png)
Работа алгоритма начинается с вычисления вспомогательного многочлена 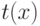 . Заметим, что из
условий, наложенных на старшие коэффициенты, следует, что
. Заметим, что из
условий, наложенных на старшие коэффициенты, следует, что 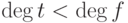 . Кроме того,
из (18.2) следует, что
. Кроме того,
из (18.2) следует, что  , поэтому
деление во второй строке выполняется нацело.
В первом цикле мы ищем многочлены
, поэтому
деление во второй строке выполняется нацело.
В первом цикле мы ищем многочлены 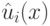 в виде
в виде 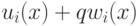 , для чего
находим
, для чего
находим  , такие, что
, такие, что 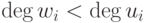 и
и
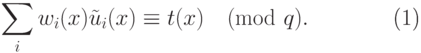 |
( 18.5) |
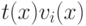 , но для них не
выполняется ограничение по степеням. При переходе от
, но для них не
выполняется ограничение по степеням. При переходе от 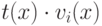 к его остатку от деления на
к его остатку от деления на 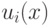 значение
соответствующего слагаемого по модулю
значение
соответствующего слагаемого по модулю 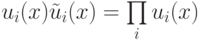 не изменится. Выполнение равенства (18.5) после
замены всех полиномов
не изменится. Выполнение равенства (18.5) после
замены всех полиномов 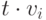 соответствующими остатками следует из того, что степени и
левой,
и правой его части меньше степени полинома
соответствующими остатками следует из того, что степени и
левой,
и правой его части меньше степени полинома  .
.По завершении работы первого цикла многочлены 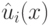 найдены, и мы переходим к модификации полиномов
найдены, и мы переходим к модификации полиномов  . Снова вводим вспомогательный многочлен
. Снова вводим вспомогательный многочлен 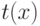 .
Из условий(18.3) следует, что
.
Из условий(18.3) следует, что 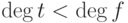 ,
а
из (18.4) - что
,
а
из (18.4) - что 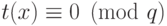 , так что
в следующей строке
деление выполняется нацело.
, так что
в следующей строке
деление выполняется нацело.
В цикле мы ищем многочлены 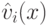 в виде
в виде 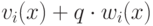 , для
чего находим
, для
чего находим  , такие, что
, такие, что 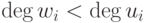 и
и
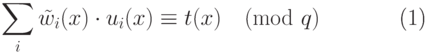 |
( 18.6) |
Условию (18.6) удовлетворяют полиномы 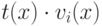 , но для них
не выполняется ограничение по степеням; при переходе от
, но для них
не выполняется ограничение по степеням; при переходе от 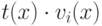 к его остатку от деления на
к его остатку от деления на 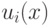 значение
соответствующего слагаемого по модулю
значение
соответствующего слагаемого по модулю 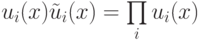 не изменится. Выполнение равенства (18.6) после замены всех
полиномов
не изменится. Выполнение равенства (18.6) после замены всех
полиномов 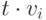 соответствующими остатками следует из того, что степени и левой, и
правой его части меньше степени полинома
соответствующими остатками следует из того, что степени и левой, и
правой его части меньше степени полинома  .
.
