|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Опубликован: 04.03.2008 | Доступ: свободный | Студентов: 1663 / 67 | Оценка: 4.56 / 3.67 | Длительность: 30:07:00
ISBN: 978-5-9556-0099-4
Специальности: Программист, Математик
Лекция 8:
Разложение многочленов на неприводимые множители по модулю p. Лемма Гензеля
Алгоритм Берлекэмпа
А28. АЛГОРИТМ (нулевое_приближение_разложения).
![\begin{equation*}
\text{Дано: \quad $p$- простое число,}\\
\text{\qquad $f(x)\in\mathbb Z[x]$ свободен от квадратов по модулю
$p$ }\\
\text{Надо:\qquad $U$ - разложение $f$ на неприводимые над полем $F_p$ }\\
\text{Обозначения:\quad $t=U.$число\_множителей} \\
\text{\qquad $n=f.$степень } \\
\text{\qquad $u=U.$множители } \\
\text{\qquad $\cI$- единичная $n{\times}n$-матрица} \\
\text{Переменные: \qquad $\EuScript Q $ - матрица $(n\times n)$ элементов поля $F_p$} \\
\text{\qquad $m,r\in\mathbb Z$ } \\
\text{ \qquad $v$ - вектор элементов типа $F_p[x]$ с индексом $1..r$}\\
\text{Начало} \\
\text{сформировать матрицу $\EuScript Q $} \\
\text{базис нуль-пространства матрицы $(n,\EuScript Q -\cI,r,v)$} \\
\text{$t := 1$ }\\
\text{$m := 1$} \\
\text{$u[1](x) := f(x)$ }\\
\text{цикл для $m$ от $1$ до $r$ пока $t < r$}\\
\text{\qquad цикл для $j$ от $2$ до $r$ пока $t < r$} \\
\text{\qquad \qquad цикл для $s$ от $0$ до $p-1$ пока $t < r$}\\
\text{\qquad \qquad \qquad $h(x):=НОД(u[m](x),v[j](x)-s)$}\\
\text{\qquad \qquad \qquad если $h(x)\ne 1$, то}\\
\text{\qquad \qquad \qquad \qquad если $h(x) = u[m](x)$, то} \\
\text{\qquad \qquad \qquad \qquad \qquad выход из цикла по $s$}\\
\text{\qquad \qquad \qquad \qquad иначе} \\
\text{\qquad \qquad \qquad \qquad \qquad$t := t + 1$}\\
\text{\qquad \qquad \qquad \qquad \qquad$u[t](x) := h(x)$}\\
\text{\qquad \qquad \qquad \qquad \qquad$u[m](x) := u[m](x)/h(x)$}\\
\text{\qquad \qquad \qquad \qquad конец если }\\
\text{\qquad \qquad \qquad конец если }\\
\text{\qquad \qquad конец цикла} \\
\text{\qquad конец цикла }\\
\text{конец цикла }\\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/6d064d5241bc31adddbed0bba62151ee.png)
Заметим, что для сравнительно небольших  (когда мы можем хранить таблицу обратных элементов для всех элементов поля
(когда мы можем хранить таблицу обратных элементов для всех элементов поля 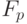 ) сложность
алгоритма Берлекэмпа оценивается величиной
) сложность
алгоритма Берлекэмпа оценивается величиной  .
.
Детализацию этого алгоритма начнем с рассмотрения предписания "базис нуль
пространства матрицы  ".
".
А29. АЛГОРИТМ (базис_нуль_пространства_матрицы).
![\begin{equation}
\text{Дано:\quad $\EuScript Q$ - матрица}\\
\text{ \qquad $n$ - размерность матрицы $\EuScript Q$ }\\
\text{Надо:\qquad $r$ - размерность нуль-пространства матрицы $\EuScript Q$}\\
\text{\qquad $v$ - (вектор элементов типа $F_p$ с""}\\
\text{индексом $0..n-1$) с индексом $1..r$, т.е линейно независимые}\\
\text{векторы $v[1],\dots, v[r]$, такие, что $v[j]\cdot\EuScript Q =\vec 0$}\\
\text{записываем $v$ в виде матрицы с индексами $1..r$, $0..n-1$}}} \\
\text{Переменные:\quad $c$ - вектор элементов типа $\mathbb Z$ с индексом $1..n$ }\\
\text{\qquad \qquad $c[j]\ge 0 \iff q_{c[j],j}= -1$,}\\
\text{\qquad \qquad все остальные элементы этой строки = 0}
\end{equation}](/sites/default/files/tex_cache/8c89cac36f5f4d99e4388d5753c1a8b4.png)
![\begin{equation}
\text{Идеи реализации: приведение к треугольному виду операциями }\\
\text{ со столбцами, т.е. переход от $\EuScript Q$ к $\EuScript Q\times B$,} \\
\text{где $B$ - невырожденная матрица }\\
\text{Начало}\\
\text{$r := 0$ }\\
\text{цикл для $j$ от $0$ до $n-1$}\\
\text{\qquad $c[j] := -1$} \\
\text{конец цикла}\\
\text{цикл для $k$ от $0$ до $n-1$\qquad //поиск зависимости строк}\\
\text{\qquad если $\exists j\colon 0\le j<n$, такое, что $\EuScript Q[k,j]\ne0$ и $c[j] <0$, то}\\
\text{\qquad \qquad умножить $j$-ый столбец матрицы $\EuScript Q$ на $-1/Q[k,j]$}\\
\text{\qquad \qquad цикл для $i$ от $0$ до $j-1$ и от $j+1$ до $n-1$}\\
\text{\qquad \qquad \qquad цикл для $l$ от $0$ до $n-1$}\\
\text{\qquad \qquad \qquad \qquad $\EuScript Q[l,i] := \EuScript Q[l,i] + \EuScript Q[k,i]\cdot \EuScript Q[l,j]$}\\
\text{\qquad \qquad \qquad конец цикла}\\
\text{\qquad \qquad \qquad $c[j] := k$}\\
\text{\qquad \qquad \qquad \qquad // эти операции не меняют строк матрицы с}\\
\text{\qquad \qquad \qquad \qquad // номерами $0,1,\dots,k-1$, т.к. $\EuScript Q[s,j]
= 0$}\\
\text{\qquad \qquad \qquad \qquad // для всех $s < k$}\\
\text{\qquad \qquad конец цикла}\\
\text{\qquad иначе \qquad // матрица $\EuScript Q$ приведена к ступенчатому виду}\\
\text{\qquad \qquad $r := r+1$ \qquad }\\
\text{\qquad \qquad \qquad \qquad // начинаем нахождение собственных векторов}\\
\text{\qquad \qquad цикл для $j$ от $0$ до $n-1$}\\
\text{\qquad \qquad \qquad $v[r,j] := 0$}\\
\text{\qquad \qquad конец цикла}\\
\text{\qquad \qquad цикл для $s$ от $0$ до $n-1$}\\
\text{\qquad \qquad \qquad $j:= c[s]$}\\
\text{\qquad \qquad \qquad если $j\ge0$, то $v[r,j] :=\EuScript Q[k,s]$ конец если}\\
\text{\qquad \qquad конец цикла}\\
\text{\qquad \qquad $v[r,k] := 1$}\\
\text{\qquad конец если}\\
\text{конец цикла}\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/8a5653310b355979a2baaf27e245197c.png)
