|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Редуцированные базисы решетки. Редуцирование базиса в решетке
Редуцирование базиса в решетке
В этом параграфе рассмотрим алгоритм построения редуцированного базиса решетки, полученный в работе [ 24 ] . Определение решетки и редуцированного базиса приведены в параграфе 19. Там же описаны основные свойства редуцированных базисов, которые понадобятся нам в алгоритмах факторизации многочленов.
Ниже сформулирован и обоснован алгоритм построения редуцированного
базиса
решетки. Построение редуцированного базиса ведем, последовательно присоединяя
очередной (  -ый) элемент исходного базиса решетки и
редуцируя базис
подрешетки, натянутой на векторы с 1-го по
-ый) элемент исходного базиса решетки и
редуцируя базис
подрешетки, натянутой на векторы с 1-го по  -ый. Алгоритм
содержит два
основных шага: на одном из них мы из присоединяемого вектора вычитаем целые
кратные векторов, уже включенных в редуцированный базис, чтобы обеспечить
выполнение условия (19.4). При этом длина редуцированной части
базиса не
меняется. Второй шаг, направленный на выполнение условия 19.5,
сводится к
перестановке добавляемого вектора с последним вектором, уже включенным в
редуцированный
базис, при такой перестановке длина редуцированной части базиса уменьшается на
1. Переменная
-ый. Алгоритм
содержит два
основных шага: на одном из них мы из присоединяемого вектора вычитаем целые
кратные векторов, уже включенных в редуцированный базис, чтобы обеспечить
выполнение условия (19.4). При этом длина редуцированной части
базиса не
меняется. Второй шаг, направленный на выполнение условия 19.5,
сводится к
перестановке добавляемого вектора с последним вектором, уже включенным в
редуцированный
базис, при такой перестановке длина редуцированной части базиса уменьшается на
1. Переменная  указывает номер элемента, который пытаемся
присоединить к
редуцированной части базиса, т.е. редуцированная часть базиса содержит в
каждый момент
указывает номер элемента, который пытаемся
присоединить к
редуцированной части базиса, т.е. редуцированная часть базиса содержит в
каждый момент  вектор. Начальное значение
вектор. Начальное значение  равно
2, т. к. любой базис
решетки, порождаемой одним вектором, является редуцированным (условия
(19.4) и
(19.5) выполняются автоматически, поскольку нет различных
индексов).
равно
2, т. к. любой базис
решетки, порождаемой одним вектором, является редуцированным (условия
(19.4) и
(19.5) выполняются автоматически, поскольку нет различных
индексов).
В описании алгоритма редуцирования базиса пользуемся типом данных
"решетка".
В отличие от принятых ранее обозначений, здесь
значения индексов принадлежат отрезку 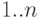 (а не
(а не 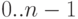 ), т.е.
), т.е.
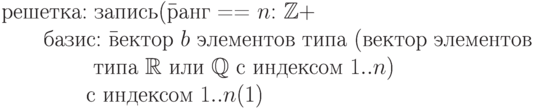
А33. АЛГОРИТМ (редуцирование-базиса).

Элементы вектора  представляют собой квадраты длин
соответствующих векторов из
ортогонального базиса
представляют собой квадраты длин
соответствующих векторов из
ортогонального базиса 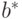 , вычисляемого по формулам (19.1)
и (19.2).
, вычисляемого по формулам (19.1)
и (19.2).
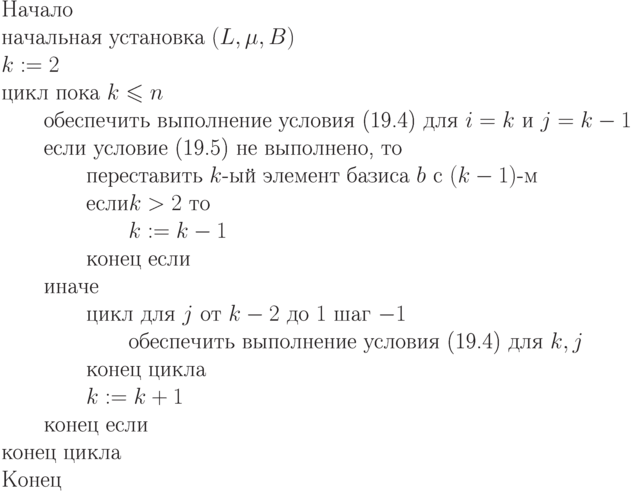
Детализируем предложенный алгоритм.
А34. АЛГОРИТМ (начальная-установка).
![\begin{equation*}\\
\text{Дано:\quad $L$-решетка}\\
\text{Надо: \qquad $\mu$ - нижняя треугольная матрица коэффициентов, }\\
\text{\qquad \qquad вычисляемых по формулам (19.1) и (19.2).}\\
\text{\qquad $B$ - вектор элементов типа $\mathbb R $ с индексом $1..n$. Элементы }\\
\text{вектора $B$ представляют собой квадраты длин }\\
\text{соответствующих векторов из ортогонального }\\
\text{базиса $b1$, вычисляемого по формулам (19.1) и (19.2).}}\\
\text{Переменные:\quad $b1$ - вектор элементов типа (вектор элементов типа }\\
\text{\qquad $\mathbb R $ с индексом $1..n$) с индексом $1..n$}\\
\text{Обозначения:
\qquad $n$ == $L$.ранг }\\
\text{\qquad $b$ == $L$.базис \ исходный базис решетки } \\
\text{\qquad $(a,b)$ == скалярное произведение векторов}\\
\text{Начало}\\
\text{цикл для $q$ от $1$ до $n$}\\
\text{\qquad $b1[q] := b[q]$}\\
\text{\qquad цикл для $l$ от $1$ до $q-1$}\\
\text{\qquad \qquad $\mu [q,l] := \dfrac{(b[q],b1[l])}{B[l]}$}\\
\text{\qquad \qquad $b1[q] := b1[q] - \mu [q,l]\cdot b1[l]$}\\
\text{\qquad конец цикла}\\
\text{\qquad $B[q] := (b1[q],b1[q])$}\\
\text{конец цикла}\\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/1be120d4a1d432e47a71ff56bf4b146e.png)
Отметим, что в предлагаемой версии алгоритма переменная  (двумерный
массив, соответствующий ортогональному базису
(двумерный
массив, соответствующий ортогональному базису 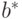 ) локальна, в
остальной
части алгоритма этот базис в явном виде не используется. Применяется вектор
) локальна, в
остальной
части алгоритма этот базис в явном виде не используется. Применяется вектор  , элементы которого представляют собой квадраты длин
ортогонального базиса,
что позволяет значительно экономить память, используемую основной программой
(вместо двумерного массива хранится одномерный). При этом нужно проследить,
как изменяются компоненты вектора
, элементы которого представляют собой квадраты длин
ортогонального базиса,
что позволяет значительно экономить память, используемую основной программой
(вместо двумерного массива хранится одномерный). При этом нужно проследить,
как изменяются компоненты вектора  при различных
выполняемых
преобразованиях, что сделано при описании соответствующих предписаний.
при различных
выполняемых
преобразованиях, что сделано при описании соответствующих предписаний.
А35. АЛГОРИТМ (обеспечить-выполнение-условия-(19.4)).
![\begin{equation*}\\
\text{Дано:\quad $L$-решетка} \\
\text{\qquad $\mu$- матрица "проекций"}\\
\text{\qquad $k>j$ - индексы}\\
\text{Надо: \qquad $\mu$-треугольная матрица коэффициентов,}\\
\text{\qquad \qquad вычисляемых по формулам (19.1) и (19.2).}\\
\text{Переменные:\quad $r$ - целое}\\
\text{Начало}\\
\text{если $| \mu [k,j]| > 1/2$ то}\\
\text{\qquad $r :=$ ближайшее целое к $\mu [k,j]$}\\
\text{\qquad $b[k] := b[k] - r\cdot b[j]$}\\
\text{\qquad цикл для $i$ от $1$ до $j-1$}\\
\text{\qquad \qquad $\mu [k,i] := \mu [k,i] - r\cdot \mu [j,i]$}\\
\text{\qquad конец цикла}\\
\text{\qquad $\mu [k,j] := \mu [k,j] - r$}\\
\text{конец если}\\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/a9f29c8e1fa62513e4822f1919297ff1.png)
Элементы нижней треугольной матрицы  вычисляются по
формулам (19.2). В
данном алгоритме меняем только вектор с индексом
вычисляются по
формулам (19.2). В
данном алгоритме меняем только вектор с индексом  . При этом
меняется только
. При этом
меняется только  -ая строка матрицы
-ая строка матрицы  , из нее вычитается
, из нее вычитается  -ая строка матрицы
-ая строка матрицы  , умноженная на
, умноженная на  . (
. (  - единичная
матрица.)
- единичная
матрица.)
Прежде чем переходить к формулировке алгоритма перестановки  -го элемента
базиса с
-го элемента
базиса с  -м, выведем соответствующие формулы. Пусть
-м, выведем соответствующие формулы. Пусть 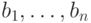 -
текущий базис, ему соответствует ортогональный базис
-
текущий базис, ему соответствует ортогональный базис 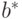 и нижняя
треугольная
матрица
и нижняя
треугольная
матрица  . Элементы нового базиса обозначим буквой
. Элементы нового базиса обозначим буквой  с соответствующим
индексом, соответствующий ортогональный базис -
с соответствующим
индексом, соответствующий ортогональный базис - 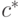 ,
нижнюю треугольную
матрицу -
,
нижнюю треугольную
матрицу - 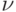 . Вычислить элементы базиса
. Вычислить элементы базиса  не
представляет труда:
не
представляет труда:
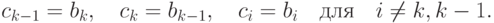 |
( 20.1) |
Переходим к вычислению ортогонального базиса. Как отмечалось выше, левая
часть
равенства (19.5) представляет собой квадрат длины ортогонального
дополнения  -го вектора к подпространству, порожденному векторами с 1-го по
-го вектора к подпространству, порожденному векторами с 1-го по 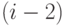 -ой.
-ой.
Таким образом,
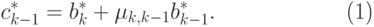 |
( 20.2) |
Для вычисления  спроектируем
спроектируем 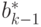 на
ортогональное дополнение
к
на
ортогональное дополнение
к 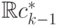 . Получим
. Получим
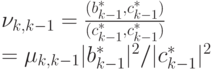 |
( 20.3) |
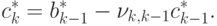 |
( 20.4) |
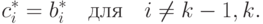 |
( 20.5) |
Для вычисления коэффициентов 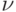 нам понадобится
выразить старый
ортогональный базис через новый. Из соотношений (20.2), (20.3) и
(20.4) получаем
нам понадобится
выразить старый
ортогональный базис через новый. Из соотношений (20.2), (20.3) и
(20.4) получаем
 |
( 20.6) |
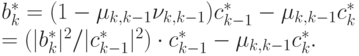 |
( 20.7) |
Подставив соотношения (20.1)-(20.7)в формулу (19.1) и
приведя подобные члены,
получим для 
 |
( 20.8) |
 |
( 20.9) |
Наконец,
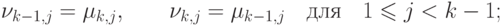 |
( 20.10) |
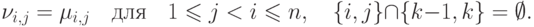 |
( 20.11) |
