|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
Инволютивные базисы
Напомним основные определения и результаты теории базисов Гребнера в простейшей постановке, т. е. для полиномиальных идеалов.
Пусть  - поле,
- поле, ![R=K[x_1,\dots,x_n]](/sites/default/files/tex_cache/36c4261752df818ff48b8459fe7f1b17.png) -
кольцо многочленов над полем
-
кольцо многочленов над полем  ,
,  - идеал
кольца
- идеал
кольца  . Как идеал
. Как идеал  , так и
фактор-кольцо
, так и
фактор-кольцо  являются линейными
являются линейными  -пространствами, в общем случае бесконечномерными. Как найти
базисы этих
пространств? В кольце
-пространствами, в общем случае бесконечномерными. Как найти
базисы этих
пространств? В кольце  , рассматриваемом как
, рассматриваемом как  -пространство, имеется базис, состоящий из множества
-пространство, имеется базис, состоящий из множества  всех мономов.
Естественно попытаться разбить множество
всех мономов.
Естественно попытаться разбить множество  на две части
на две части 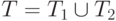 так, что образы элементов из
так, что образы элементов из  в
фактор-кольце
в
фактор-кольце  образуют базис
образуют базис  -пространства
-пространства  ,
а элементы базиса
,
а элементы базиса  -пространства
-пространства  находятся во
взаимно-однозначном
соответствии с элементами множества
находятся во
взаимно-однозначном
соответствии с элементами множества  .
.
Предположим, что на множестве мономов задан допустимый порядок, т.е.
отношение  , удовлетворяющее условиям:
, удовлетворяющее условиям:
-
 для любого нетривиального монома
для любого нетривиального монома  ;
; - если мономы
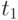 и
и 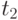 удовлетворяют соотношению
удовлетворяют соотношению 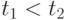 , то
, то  для любого монома
для любого монома  .
.
Таким образом для любого многочлена  можно определить его старший моном
можно определить его старший моном 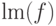 и старший
коэффициент
и старший
коэффициент  , и множество мономов
, и множество мономов  разбивается на два
подмножества:
разбивается на два
подмножества:  состоит из мономов, которые не являются старшими
мономами ни для одного элемента
состоит из мономов, которые не являются старшими
мономами ни для одного элемента  , и
, и  состоит из мономов, которые являются старшими мономами для элементов из
состоит из мономов, которые являются старшими мономами для элементов из  .
.
Теперь возникает вопрос: как описать множества  и
и  конструктивно?
конструктивно?
Ответ на него, а также на многие другие вопросы конструктивной теории
полиномиальных идеалов, дает теория базисов Гребнера. Имеется несколько
эквивалентных определений базисов Гребнера (см.,
[
26
]
или
[
16
]
, в
[
14
]
стр.40] эти определения рассматриваются с учетом
выбора алгоритма нормальной формы). Например, множество  называется базисом Гребнера идеала
называется базисом Гребнера идеала  , если любой элемент
, если любой элемент  допускает представление вида
допускает представление вида 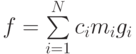 , где
, где  ,
, 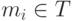 ,
, 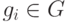 и выполнено условие
и выполнено условие 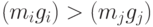 при
при  (представление такого вида называется
(представление такого вида называется  -представлением). Это
определение, во-первых, не является конструктивным, во-вторых, определяет
базис Гребнера неоднозначно. Конструктивный метод построения базиса Гребнера
дает алгоритм пополнения (см.упражнение 9.38). Для того, чтобы выделить из всех
базисов Гребнера некоторый однозначно определенный, введем понятие
авторедуцированного множества.
-представлением). Это
определение, во-первых, не является конструктивным, во-вторых, определяет
базис Гребнера неоднозначно. Конструктивный метод построения базиса Гребнера
дает алгоритм пополнения (см.упражнение 9.38). Для того, чтобы выделить из всех
базисов Гребнера некоторый однозначно определенный, введем понятие
авторедуцированного множества.
Множество многочленов 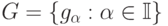 называется авторедуцированным,
если для любого
называется авторедуцированным,
если для любого  ни один из одночленов,
входящих в
ни один из одночленов,
входящих в 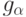 с ненулевым коэффициентом, не делится ни на
один из
мономов
с ненулевым коэффициентом, не делится ни на
один из
мономов 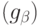 для
для  . Базис
Гребнера, который
является авторедуцированным множеством и старшие коэффициенты элементов
которого равны 1, определен однозначно для любого идеала
. Базис
Гребнера, который
является авторедуцированным множеством и старшие коэффициенты элементов
которого равны 1, определен однозначно для любого идеала  .
Назовем такой
базис авторедуцированным базисом Гребнера.
.
Назовем такой
базис авторедуцированным базисом Гребнера.
Предположим, что мы знаем авторедуцированный базис Гребнера  идеала
идеала  . Чтобы получить базис
. Чтобы получить базис  как линейного
пространства, нам достаточно указать процедуру, которая каждому моному
как линейного
пространства, нам достаточно указать процедуру, которая каждому моному  ставит в соответствие некоторый элемент
ставит в соответствие некоторый элемент  , старший моном которого делит
, старший моном которого делит  , т.е.
, т.е. 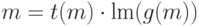 для некоторого монома
для некоторого монома 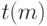 .
Тогда множество
многочленов
.
Тогда множество
многочленов 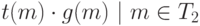 образует базис линейного
пространства
образует базис линейного
пространства  . Любую такую процедуру назовем алгоритмом нормальной формы.
. Любую такую процедуру назовем алгоритмом нормальной формы.
10.1. ПРИМЕР.
Простейший алгоритм нормальной формы состоит в том, что элементы
авторедуцированного базиса Гребнера нумеруются в каком-либо
порядке индексами от 1 до  и каждому моному
и каждому моному 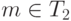 ставится в соответствие элемент
ставится в соответствие элемент  с минимальным
индексом, такой,
что
с минимальным
индексом, такой,
что 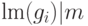 . Существуют, однако, и более сложные алгоритмы
нормальной формы.
. Существуют, однако, и более сложные алгоритмы
нормальной формы.
Рассмотрим этот пример подробнее. Пусть авторедуцированный базис Гребнера
идеала  состоит из многочленов
состоит из многочленов 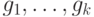 . Тогда
базис линейного пространства
. Тогда
базис линейного пространства  получается объединением следующих
множеств множества
получается объединением следующих
множеств множества  всех произведений
всех произведений 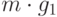 , где
, где 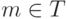 ;
множества
;
множества 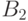 произведений
произведений 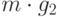 , таких, что
, таких, что  ;
множества
;
множества 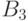 произведений
произведений 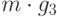 , таких, что
, таких, что  ;
;  множества
множества 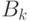 произведений
произведений  , таких, что
, таких, что 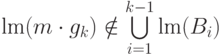 .
.
Этот же базис можно описать несколько по-другому.
Для каждого  выделим максимальное подмножество переменных
выделим максимальное подмножество переменных 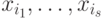 такое, что произведение
такое, что произведение  на
любой моном, включающий только эти переменные (обозначим множество таких мономов
на
любой моном, включающий только эти переменные (обозначим множество таких мономов 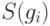 ), принадлежит
), принадлежит 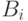 .
Назовем эти переменные мультипликативными
для монома
.
Назовем эти переменные мультипликативными
для монома 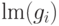 ,
остальные переменные назовем немультипликативными.
Исключим из
,
остальные переменные назовем немультипликативными.
Исключим из 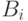 моном
моном  и все его произведения на
мономы из
и все его произведения на
мономы из 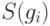 . Если полученное множество непусто, то возьмем в
нем
младший моном
. Если полученное множество непусто, то возьмем в
нем
младший моном 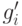 и повторим процесс для него.
Таким образом мы
можем представить базис линейного пространства
и повторим процесс для него.
Таким образом мы
можем представить базис линейного пространства  в виде
объединения конечного набора множеств, каждое из которых
описывается некоторым многочленом и набором мультипликативных переменных для
этого многочлена. Полученный базис представляет собой
пример инволютивного базиса. В коммутативную алгебру понятие инволютивного базиса было
введено Жарковым и Блинковым
[
8
]
,
[
30
]
.
в виде
объединения конечного набора множеств, каждое из которых
описывается некоторым многочленом и набором мультипликативных переменных для
этого многочлена. Полученный базис представляет собой
пример инволютивного базиса. В коммутативную алгебру понятие инволютивного базиса было
введено Жарковым и Блинковым
[
8
]
,
[
30
]
.
Итак, для построения инволютивного базиса мы воспользовались базисом Гребнера, алгоритмом нормальной формы и процедурой разделения переменных на мультипликативные и немультипликативные для некоторого набора мономов.
Напомним алгоритмы проверки того, что заданное множество является базисом
Гребнера порождаемого им идеала и построения базиса Гребнера
по заданной системе образующих идеала  (этот алгоритм называется алгоритмом пополнения ).
(этот алгоритм называется алгоритмом пополнения ).
Пусть дано множество многочленов  и отношение порядка на
множестве мономов
и отношение порядка на
множестве мономов  . Для проверки того, что
. Для проверки того, что  является базисом
Гребнера идеала
является базисом
Гребнера идеала 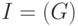 относительно порядка <,
используется некоторый алгоритм нормальной формы, от выбора которого результат
не зависит. Алгоритм состоит в том, что формируется множество
относительно порядка <,
используется некоторый алгоритм нормальной формы, от выбора которого результат
не зависит. Алгоритм состоит в том, что формируется множество  -полиномов и проверяется, что каждый из этих полиномов
редуцируется к нулю. Для повышения эффективности алгоритма используются
различные критерии, позволяющие сузить круг
рассматриваемых
-полиномов и проверяется, что каждый из этих полиномов
редуцируется к нулю. Для повышения эффективности алгоритма используются
различные критерии, позволяющие сузить круг
рассматриваемых  -полиномов, например, "правило
треугольника".
-полиномов, например, "правило
треугольника".
