Численное решение систем линейных алгебраических уравнений
Теорема (достаточное условие сходимости метода Якоби ) Итерационный метод Якоби сходится к решению соответствующей СЛАУ, если выполнено условие диагонального преобладания
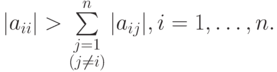 |
( 2.24) |
Доказательство.
Выполненные условия (2.24) означает, что в любой строке матрицы перехода
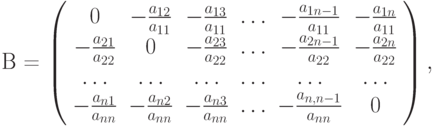
сумма модулей элементов меньше единицы. В этом случае по крайней мере одна из норм матрицы  меньше единицы. Тогда выполняется достаточное условие сходимости метода простых итераций.
меньше единицы. Тогда выполняется достаточное условие сходимости метода простых итераций.
Теорема (критерий сходимости итерационного метода Якоби ). Для сходимости итерационного метода Якоби необходимо и достаточно, чтобы все корни уравнения
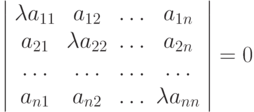
по модулю не превосходили единицы.
Доказательство.
Легко проверить, что в силу диагональности 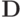 имеет место
имеет место
![\det ({\mathbf{B}}- \lambda {\mathbf{E}}) = \det \left[{-{\mathbf{D}}^{- 1}({\mathbf{L}} + {\mathbf{U}}) - \lambda {\mathbf{E}}}\right] = \det ( -{\mathbf{D}}^{-
1}) \cdot \det \left[{({\mathbf{L}} + {\mathbf{U}}) +{\mathbf{D}}\lambda}\right].](/sites/default/files/tex_cache/115fb03963ebe4d5d46e74edd8ee3ce7.png)
Собственными значениями матрицы 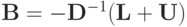 являются корни уравнения
являются корни уравнения
![\det \left[{({\mathbf{L}}+{\mathbf{U}}) + {\mathbf{D}}\lambda}\right] = 0,](/sites/default/files/tex_cache/5c6fc7c518ea8912b625a971e2bad0bf.png)
которые в соответствии с критерием сходимости метода простой итерации должны быть по модулю меньше единицы.
Аналогичную теорему можно доказать и для метода Зейделя, однако матрица в этой теореме будет иметь другой вид:
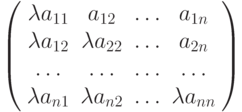
Теорема (достаточное условие сходимости метода Зейделя (без доказательства)). Пусть  — вещественная, симметричная, положительно определенная матрица. В этом случае итерационный метод Зейделя сходится.
— вещественная, симметричная, положительно определенная матрица. В этом случае итерационный метод Зейделя сходится.
Доказательство этой теоремы сводится к проверке того, что выполнение
условий теоремы для матрицы 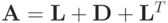 влечет выполнение условия сходимости итерационного метода с матрицей перехода —
влечет выполнение условия сходимости итерационного метода с матрицей перехода —  СЛАУ с вещественной матрицей
СЛАУ с вещественной матрицей  такой, что
такой, что  может быть симметризована умножением на матрицу
может быть симметризована умножением на матрицу 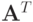 :
:
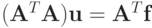
(симметризация Гаусса).
Развитием метода Зейделя является метод релаксации. В этом методе вводится
итерационный параметр 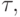 называемый параметром релаксации.
Представим метод релаксации в матричной форме:
называемый параметром релаксации.
Представим метод релаксации в матричной форме:
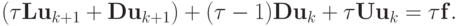
Выбирая 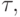 можно существенно изменять скорость сходимости итерационного метода. Выразим
можно существенно изменять скорость сходимости итерационного метода. Выразим 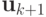
![{\mathbf{u}}_{k + 1} = - ({\mathbf{D}} + \tau{\mathbf{L}})^{- 1}\left[{(\tau - 1)
{\mathbf{D}} + \tau{\mathbf{L}}}\right]{\mathbf{u}}_k + \tau ({\mathbf{D}}+ \tau
{\mathbf{L}})^{- 1}\mathbf{f}.](/sites/default/files/tex_cache/0d055342817f0429a51cf6ed49857b10.png)
В общем случае задача вычисления 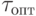 (оптимального итерационного параметра) не решена, однако известно, что
(оптимального итерационного параметра) не решена, однако известно, что  В этом случае итерационный метод называется методом последовательной верхней релаксации или SОR — Successive Over Relaxation. Иногда встречается термин "сверхрелаксация" при
В этом случае итерационный метод называется методом последовательной верхней релаксации или SОR — Successive Over Relaxation. Иногда встречается термин "сверхрелаксация" при  При
При 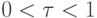 имеем метод нижней релаксации.
имеем метод нижней релаксации.
