Численное решение систем линейных алгебраических уравнений
2.4.2. Модификация метода Гаусса для случая линейных систем с трехдиагональными матрицами — метод прогонки
В приложениях часто возникают системы линейных уравнений с матрицами специального вида. В дальнейшем, например, при интерполяции функции сплайнами, при решении задачи Штурма-Лиувилля, при численном решении уравнений теплопроводности, уравнений Лапласа и Пуассона придется иметь дело с системами, матрицы которых имеют ненулевые элементы лишь на главной диагонали и еще на двух диагоналях — одной под главной, одной над главной. Такие матрицы называются трехдиагональными. Для решения систем с трехдиагональными матрицами существует экономичный (требующий малого количества памяти и арифметических действий) вариант метода Гаусса — прогонка. В англоязычной литературе метод прогонки называется алгоритмом Томаса. Подробнее о свойствах метода прогонки речь пойдет в "Численное решение краевых задач для систем обыкновенных дифференциальных уравнений" в связи с решением разностными методами задачи Штурма-Лиувилля.
2.4.3. LU-разложение
Среди прямых методов численного решения СЛАУ широко используется также LU-разложение матрицы  и метод Холецкого (или метод квадратного корня).
и метод Холецкого (или метод квадратного корня).
Если матрица  представима в виде произведений матриц
представима в виде произведений матриц 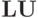 , то СЛАУ может быть представлена в виде
, то СЛАУ может быть представлена в виде
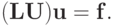 |
( 2.13) |
Перепишем (2.13), вводя вспомогательный вектор  , в следующем виде
, в следующем виде
 |
( 2.14) |
Решение СЛАУ свелось к последовательному решению двух систем с треугольными
матрицами. Первый этап решения системы 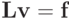 :
:
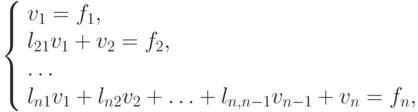
откуда можно вычислить все vk последовательно по формулам

Далее рассмотрим систему 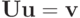 или
или
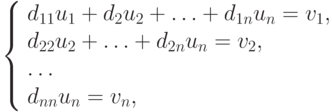
решение которой находится в обратном порядке, т.е. при k = n - 1, ..., 1 по очевидным формулам 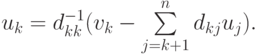 Условия существования такого разложения даются следующей
теоремой [2.5] (без доказательства).
Условия существования такого разложения даются следующей
теоремой [2.5] (без доказательства).
Теорема. Если все главные миноры квадратной матрицы  отличны от нуля, то существуют единственные
нижняя и верхняя треугольные матрицы
отличны от нуля, то существуют единственные
нижняя и верхняя треугольные матрицы 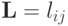 и
и 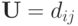 такие, что
такие, что  При этом все диагональные коэффициенты матрицы
При этом все диагональные коэффициенты матрицы 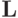 фиксированы и равны единице.
фиксированы и равны единице.
Опишем алгоритм нахождения элементов lijdij матриц 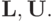 Выписав равенство
Выписав равенство  в компонентах, получим
в компонентах, получим
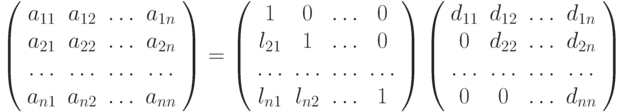
Выполнив умножение матриц, приходим к системе линейных уравнений размером n x n:
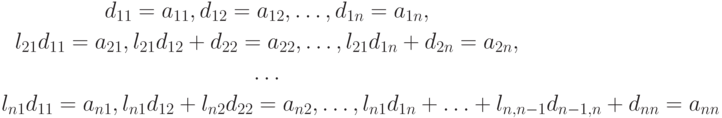
относительно неизвестных d11, d12, ..., d1n, l21, d22, ..., d2n, ln1, ln2, ..., dnn.
Специфика этой системы позволяет решить ее последовательно. Из первой строки находим d1j= a1j(j = 1, ..., n).
Из уравнений, входящих в первый столбец приведенной выше системы, находим li1= ai1/d11, i = 1, ...dots, n. Теперь можно из уравнений второй строки найти d2j= a2j- l21d1j, j = 2, ..., n, а из уравнений, входящих во второй столбец, получим 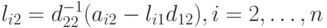 и так далее. Последним вычисляется элемент
и так далее. Последним вычисляется элемент
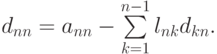
Можно выписать общий вид этих формул:
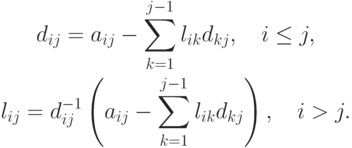
Приведение матриц к треугольному виду аналогично приведению матрицы в методе Гаусса и также требует количества арифметических действий порядка O(n3), точнее, 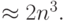
2.4.4. Метод Холецкого (метод квадратного корня)
Пусть матрица рассматриваемой линейной системы  — симметричная, т.е. aij = aji, положительная матрица. Тогда она представима в виде
— симметричная, т.е. aij = aji, положительная матрица. Тогда она представима в виде  , где
, где
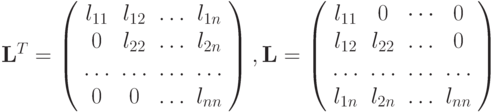
Далее, как и в случае LU-разложения, решение СЛАУ 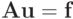 сводится к последовательному решению двух линейных систем с треугольными матрицами
сводится к последовательному решению двух линейных систем с треугольными матрицами 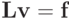 ,
,  , для решения которых требуется примерно 2n2 арифметических действий.
, для решения которых требуется примерно 2n2 арифметических действий.
Первая из этих линейных систем
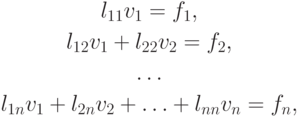
она легко решается. Для решения получаем очевидные формулы
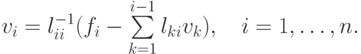
Вторая система уравнений есть
l11u1 + l12u2 + ... + l1nun = v1 , l22u2 + ... + l2nun = v2, ... lnnun = vn.
Из нее находим значения переменных ui в обратном порядке по формуле
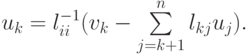
Определенной опасностью при реализации этого метода являются возможная
близость к нулю lii и отрицательность подкоренных выражений при вычислении lii (последнего не должно быть при симметричной положительной матрице  )
)
Элементы матрицы  находим из уравнения
находим из уравнения 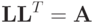 , приравнивая соответствующие элементы матриц
, приравнивая соответствующие элементы матриц  и
и  В результате получим систему уравнений
В результате получим систему уравнений
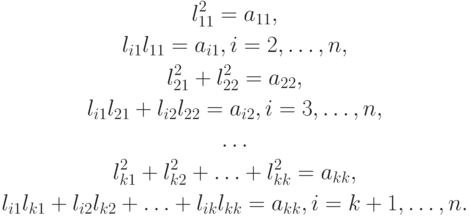
Решение этой системы легко находится:
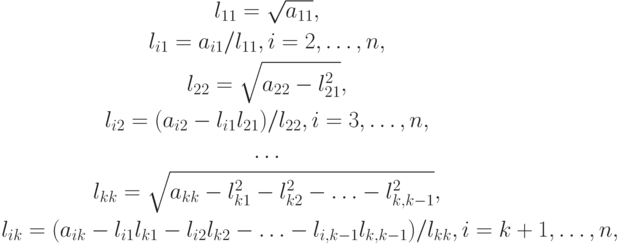
Метод также называется методом квадратного корня.
Внимание! Не следует путать матрицу (оператор) 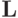 с
оператором
с
оператором 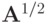 — квадратным корнем из самосопряженного положительного оператора.
— квадратным корнем из самосопряженного положительного оператора.
