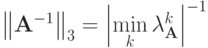Численное решение систем линейных алгебраических уравнений
2.3. Обусловленность СЛАУ. Число обусловленности матрицы
Понятия согласованных норм матриц и векторов позволяют оценить погрешности, возникающие при численном решении СЛАУ. Пусть и матрица, и правая часть системы заданы с некоторой погрешностью, тогда наряду с системой
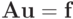 |
( 2.4) |
рассматривается система
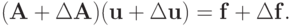 |
( 2.5) |
Теорема. Пусть правая часть и невырожденная матрица СЛАУ (2.4)
вида  , получили приращения
, получили приращения 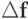 и
и  соответственно. Пусть существует обратная матрица
соответственно. Пусть существует обратная матрица 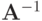 и выполнены условия
и выполнены условия
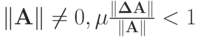
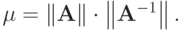 В этом случае оценка относительной погрешности решения
В этом случае оценка относительной погрешности решения 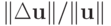 удовлетворяет
неравенству
удовлетворяет
неравенству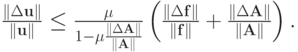
Доказательство.
Из (2.5) следует, что 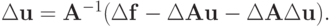 Переходя в этом равенстве к норме и использовав неравенство треугольника, получаем
Переходя в этом равенстве к норме и использовав неравенство треугольника, получаем

Вводя обозначение  , перепишем последнее равенство в виде
, перепишем последнее равенство в виде
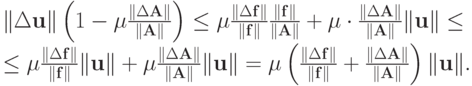
Заметим, что


Тогда для оценки относительной погрешности решения окончательно получим
 |
( 2.6) |
При 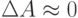 получаем оценку при наличии погрешности только правых частей
получаем оценку при наличии погрешности только правых частей
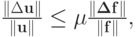 |
( 2.7) |
если в (2.5) положить 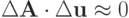 , то
, то
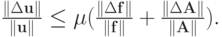 |
( 2.8) |
В результате получено важное соотношение, показывающее, на сколько возрастают относительные ошибки решения СЛАУ в случае наличия относительных ошибок при задании правых частей и элементов матриц.
Величина
 |
( 2.9) |
называется числом обусловленности матрицы  Число обусловленности определяет, насколько погрешность входных данных может повлиять на решение системы (2.1) . Почти очевидно, что всегда
Число обусловленности определяет, насколько погрешность входных данных может повлиять на решение системы (2.1) . Почти очевидно, что всегда 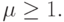 Действительно
Действительно
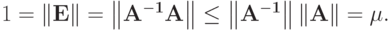
При 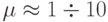 ошибки входных данных слабо сказываются на решении и система (2.1) считается хорошо обусловленной. При
ошибки входных данных слабо сказываются на решении и система (2.1) считается хорошо обусловленной. При  система является плохо обусловленной.
система является плохо обусловленной.
Пример. Решением системы
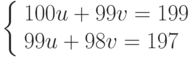
будет пара чисел u = v = 1.
Внесем возмущение в правые части системы:
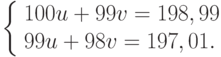
При этом решение заметно изменится: u = 2,97; v = -0,99. Воспользовавшись выбранными согласованными нормами, получим
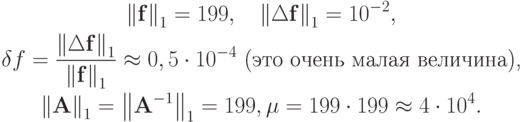
Значит,
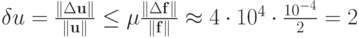
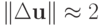 ,
, 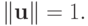
Рассмотрим еще одно важное свойство. Число обусловленности матрицы, как
было показано ранее, можно определить, как  , если
, если 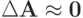 при
при
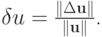
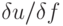 , учитывающую зависимость обусловленности СЛАУ от выбора правых частей? В этом случае параметр обусловленности системы, вообще говоря, зависит и от
, учитывающую зависимость обусловленности СЛАУ от выбора правых частей? В этом случае параметр обусловленности системы, вообще говоря, зависит и от 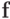 , и
от
, и
от 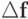 , и удовлетворяет неравенству
, и удовлетворяет неравенству 
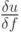
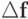 , что соответствует наихудшей ситуации. Тогда
, что соответствует наихудшей ситуации. Тогда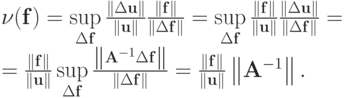
Далее,
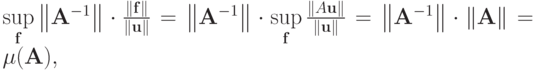
с другой стороны

Параметр 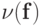 , характеризующий обусловленность системы, зависит от правых частей. Более тонкая его оценка есть
, характеризующий обусловленность системы, зависит от правых частей. Более тонкая его оценка есть
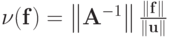
 Так как такую оценку провести не всегда возможно, то чаще используется точная верхняя грань
Так как такую оценку провести не всегда возможно, то чаще используется точная верхняя грань 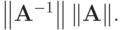 Такая оценка, конечно, может быть существенно завышенной.
Такая оценка, конечно, может быть существенно завышенной.Можно также показать, что для симметричной матрицы  имеет место
имеет место 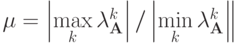 , т.е. обусловленность СЛАУ зависит от ее спектральных свойств. Это следует из определения третьей нормы матрицы
, т.е. обусловленность СЛАУ зависит от ее спектральных свойств. Это следует из определения третьей нормы матрицы 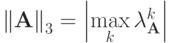 и соотношения
и соотношения