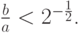Численное решение систем линейных алгебраических уравнений
Задачи
-
Методом Гаусса решить систему линейных уравнений
 , где
, где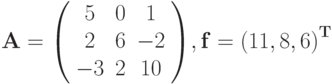
или
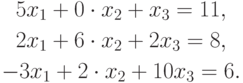
Решение.Расширенная матрица
 имеет
вид
имеет
вид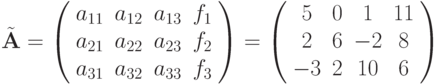
Разделив элементы первой строки на ведущий элемент a11= 5 получаем первую опорную строку (1, 0, 0.2, 2.2).
Далее умножим ее на a21= 2 и вычтем из второй строки, после чего умножим опорную строку на a31= 3 и вычтем из третьей. Получаем матрицу
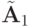
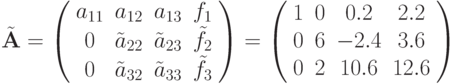
Вторая опорная строка — результат деления второй строки матрицы
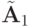 на
на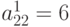 :
:(0, 1, - 0.4, 0.6)
Матрицы
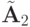 после умножения опорной строки на 2 и вычитания ее из третьей
после умножения опорной строки на 2 и вычитания ее из третьей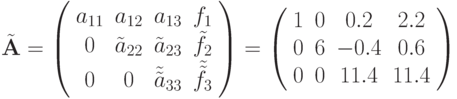
Третья опорная строка (результат деления третьей строки на 11,4 ) есть (0,0,1,1) .
Матрица
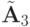 будет
будет
Обратный ход метода Гаусса.
Система уравнений с матрицей
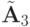
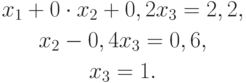
Разрешая эту систему, начиная с последнего уравнения, получим
x3 = 1, x2 = 1, x1 = 2.
Определитель матрицы
 можно вычислить как произведение ведущих элементов
можно вычислить как произведение ведущих элементов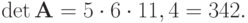
- Показать, что решение системы линейных уравнений
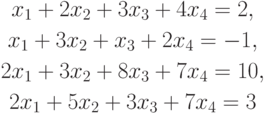
методом Гаусса невозможно.
Решение. Преобразование матрицы рассматриваемой системы будет
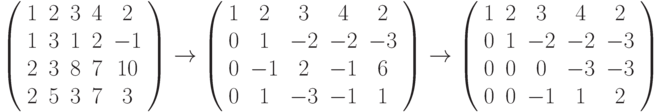
Поскольку
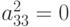 то вычисление третьей опорной строки невозможно.
то вычисление третьей опорной строки невозможно. - Показать, что
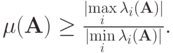
Рассмотреть случай симметричной матрицы

Решение. Для собственного вектора
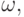 соответствующего наибольшему по модулю собственному значению матрицы, выполняется равенство
соответствующего наибольшему по модулю собственному значению матрицы, выполняется равенство 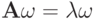 , откуда
, откуда
Учитывая, что
 , получим
, получим 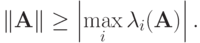 Для обратной матрицы
Для обратной матрицы 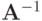 максимальным по модулю является собственное число
максимальным по модулю является собственное число 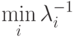 , откуда
, откуда 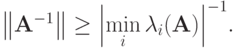 Объединяя два последних
неравенства, получим
Объединяя два последних
неравенства, получим
В случае симметричной матрицы
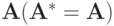 имеем
имеем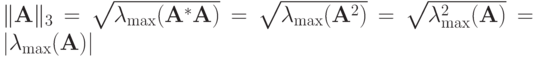 ,
,т.к. из
 следует
следует 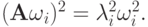 Аналогично
Аналогично![{\left\|{\mathbf{A}^{- 1}}\right\|}_3 = \sqrt{\lambda_{\max}[(\mathbf{A}^{- 1})^*
(\mathbf{A}^{- 1})]} = \sqrt{\lambda_{\max}[(\mathbf{A}^{- 1})]^2} = \\
= \sqrt{\lambda_{\min}^{- 1}(\mathbf{A}^2 )} = |{\lambda_{\min}^{- 1}(\mathbf{A})}|.](/sites/default/files/tex_cache/ce7c669e933218961f946e66274d417c.png)
Тогда

- Найти число обусловленности матрицы
 , выразив его
через число обусловленности матрицы
, выразив его
через число обусловленности матрицы 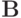 , если
, если 
Решение. Для самосопряженной положительной матрицы
 имеем
имеем
Тогда
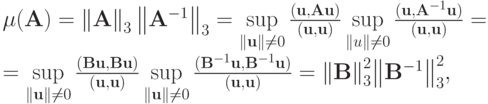
откуда

- Показать, что норма матрицы

согласована с нормой вектора

Решение.
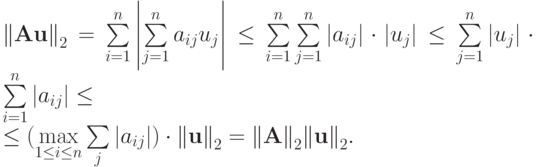
Положим

Покажем, что существует вектор
 , для которого достигается равенство. В качестве такового можно взять вектор
, для которого достигается равенство. В качестве такового можно взять вектор  с компонентами
с компонентами 
Таким образом, норма матрицы
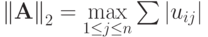 согласована с нормой вектора
согласована с нормой вектора 
- Дана жорданова клетка порядка n
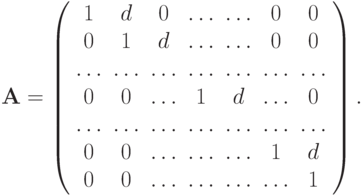
Найти
 и оценить возмущение в компоненте
и оценить возмущение в компоненте 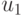 решения системы
решения системы 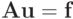 , если
компонент fn вектора f возмущен на величину
, если
компонент fn вектора f возмущен на величину 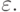
Решение. Из
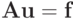 следует, что
следует, что 
С помощью обратной подстановки un = 1, un - 1 = ... находим компоненты матрицы
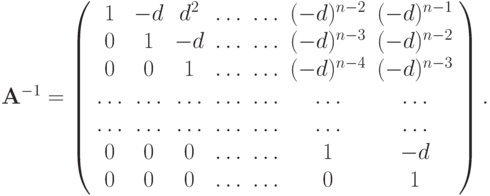
В этом случае
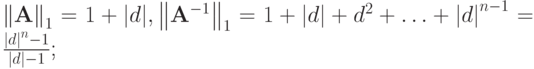
Видно, что при | d | > 1 матрица
 плохо обусловлена, при | d | < 1 - хорошо. При n = 20 и d = 5 имеем
плохо обусловлена, при | d | < 1 - хорошо. При n = 20 и d = 5 имеем 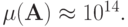
Компонент
 решения возмущенной системы
решения возмущенной системы 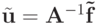 будет
будет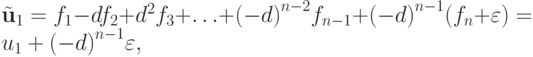
где u1 — компонент решения невозмущенной системы
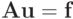
Отсюда видно, что при | d | > 1 возмущение в n компоненте вектора
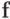 увеличивается в компоненте u1 вектора
увеличивается в компоненте u1 вектора  в | d |n - 1 раз, а при | d | < 1 — в | d |n - 1 раз убывает.
в | d |n - 1 раз, а при | d | < 1 — в | d |n - 1 раз убывает. - Пусть в системе линейных уравнений
u1 + 0,99u2 = f1, 0,99u1 + u2 = f2
вектор
 получает приращение
получает приращение 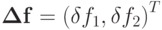 , а решение получает
приращение
, а решение получает
приращение 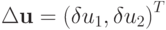 ,
Найти наименьшее число
,
Найти наименьшее число 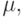 при котором независимо от
при котором независимо от 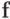 и
и 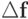 выполняется оценка
выполняется оценка
Решить задачу, используя нормы матриц

Решение. Для возмущенной задачи
 , из линейности системы
следует
, из линейности системы
следует 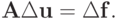 Для возмущения решения выполняется равенство
Для возмущения решения выполняется равенство  Тогда
Тогда 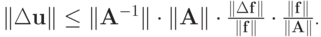
Отсюда сразу следует
, так как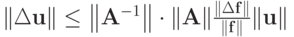
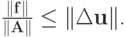
Тогда искомая оценка будет
Обозначим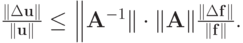
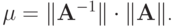 В этом случае наименьшим числом, при котором выполняется оценка , является
В этом случае наименьшим числом, при котором выполняется оценка , является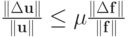
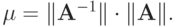 Это — число обусловленности системы уравнений. Численное решение в соответствующих нормах
получается легко.
Это — число обусловленности системы уравнений. Численное решение в соответствующих нормах
получается легко.
- При заданном фиксированном
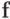 найти наименьшее
число
найти наименьшее
число 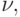 при котором независимо от
при котором независимо от 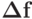 выполняется оценка
выполняется оценка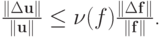
Найти такую правую часть системы
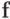 , которой соответствует
наименьшее
, которой соответствует
наименьшее 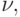 а также само это значение при использовании третьей нормы матрицы.
а также само это значение при использовании третьей нормы матрицы.Решение.
По условию задачи
Рассмотрим, какие значения может принимать это число. Точная нижняя грань для такой оценки, очевидно,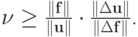 Так как надо найти оценку, не зависящую от начального возмущения (при решении конкретной задачи оно, очевидно, неизвестно), получим
Так как надо найти оценку, не зависящую от начального возмущения (при решении конкретной задачи оно, очевидно, неизвестно), получим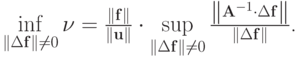
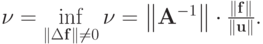
Для точной нижней грани выполнено
Можно оценить и точную верхнюю грань:
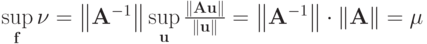
Таким образом,
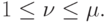
Ответим на вопрос, при каких
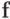 достигается
достигается 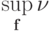 и
и  Для этого используем разложение вектора правой части системы по базису из собственных векторов матрицы
Для этого используем разложение вектора правой части системы по базису из собственных векторов матрицы 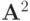 (без ограничения общности полагаем,
что такой базис существует). В этом базисе
(без ограничения общности полагаем,
что такой базис существует). В этом базисе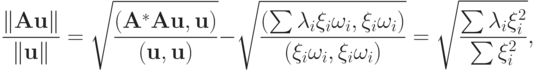
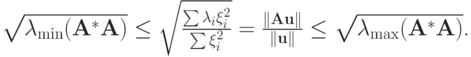
Для самосопряженной положительной матрицы
 получаем
получаем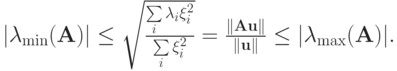
В то же время
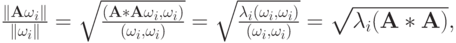
для самосопряженной положительной матрицы

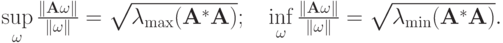
В случае
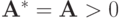 получаем
получаем 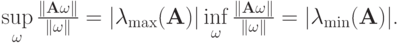
Таким образом,
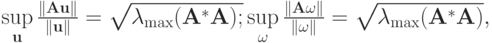
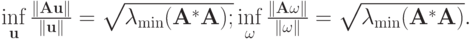
- Выписать формулы итерационных методов Якоби, Зейделя, верхней релаксации
для СЛАУ
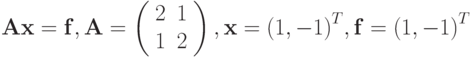
или
2u + v = 1, u + 2v = - 1.
Оценить количество итераций для метода Якоби.
(Решение системы: u = 1; v = -1 ).
Решение.
Итерационные методы Якоби, Зейделя, релаксации соответственно записываются
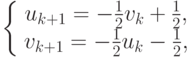
 ,
,или
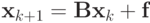 ,
,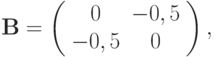

Оценка количества итераций проводится по формуле
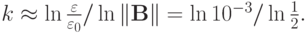
- Представить графическую интерпретацию итерационного метода Якоби для СЛАУ
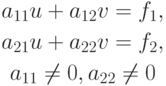
Решение. Итерационный процесс Якоби записывается как
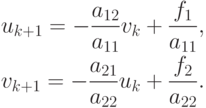
Первое уравнение соответствует прямой 1, второе — прямой 2. Вычисление u1 соответствует проведению отрезка, параллельного оси 0u и (при v = v0 ) до пересечения с прямой 1 ; точка пересечения даст первое приближение u1. Вычислению v1 соответствует проведение из точки A1 прямой, параллельной оси 0v до пересечения с прямой 2 и т.д. до сходимости итераций к точке пересечения прямых 1 и 2 (Ak) с заданной точностью.
- При каких a,b сходится метод простой итерации
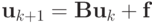 , где
, где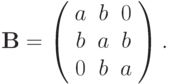
Решение. Для того, чтобы метод простой итерации сходился к решению соответствующей СЛАУ, необходимо и достаточно, чтобы все собственные значения матрицы
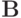 по модулю были меньше единицы:
по модулю были меньше единицы:  Решаем характеристическое уравнение
Решаем характеристическое уравнение![\begin{gather*}
det (\mathbf{B}- \lambda \mathbf{E}) =
{\left| \begin{array}{ccc}
{a - \lambda } & {b} & 0 \\
{b} & {{a}-{\lambda}} & {b}\\
0 & {b} & {{a}-{\lambda}}\\
\end{array} \right|} = \\
= (a - \lambda )
{\left| \begin{array}{cc}
{{a}-{\lambda}} & {b}\\
{b} & {{a}-{\lambda}}\\
\end{array} \right|} - b{\left| \begin{array}{cc}
{b} & {a}\\
0 & {{a}-{\lambda}}\\
\end{array} \right|} = \\
= (a - \lambda )\left[{{(a - \lambda )}^2 - b^2}\right] - b^2 (a - \lambda ) = \\
= (a - \lambda )(a - \lambda - \sqrt{2b})(a - \lambda + \sqrt{2b}) = 0,
\end{gather*}](/sites/default/files/tex_cache/fe1882964b00b7f190fb3365c1745178.png)
откуда получим условие сходимости итерационного метода

- Найти условие сходимости итерационных методов Якоби и Зейделя для СЛАУ
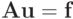 с матрицей
с матрицей вида
вида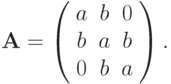
Решение. Для метода Якоби

Имеет место уравнение:
 , где
, где 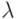 и
и 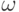 — собственное число и собственный вектор, соответственно. В таком случае
— собственное число и собственный вектор, соответственно. В таком случае  , или:
, или: 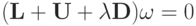 , откуда (предполагаем наличие нетривиальных решений у последней СЛАУ ):
, откуда (предполагаем наличие нетривиальных решений у последней СЛАУ ):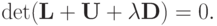
Решим это уравнение:
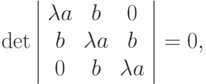
откуда получим условия сходимости итерационного метода Якоби:
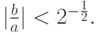
Для метода Зейделя имеем

В таком случае
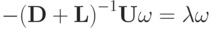 ,
,откуда следует уравнение
 ,
,Вычислив детерминант, придем к алгебраическому уравнению
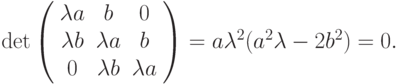
В таком случае, поскольку
, получим условие сходимости метода Зейделя: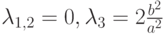 Видно, что в данном случае условия сходимости для обоих методов совпадают.
Видно, что в данном случае условия сходимости для обоих методов совпадают.