Московский государственный университет имени М.В.Ломоносова
Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5323 / 593 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00
ISBN: 978-5-9556-0038-3
Тема: Математика
Специальности: Математик
Лекция 9:
Линейное пространство строк над полем
Связь решений неоднородной системы линейных уравнений с решениями соответствующей однородной системы
Пусть
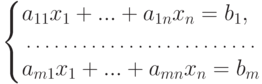
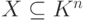 ,
,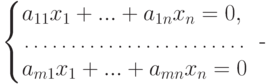
 .
.Теорема 4.2.1. Пусть 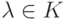 ,
,  ,
, 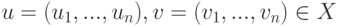 . Тогда:
. Тогда:
- если
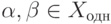 , то
, то 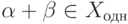 ,
, - если
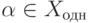 , то
, то 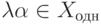 ,
, - если
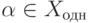 ,
, 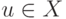 , то
, то 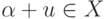 ,
, - если
 , то
, то 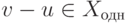 .
.
Доказательство. Для любого i, 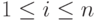 :
: 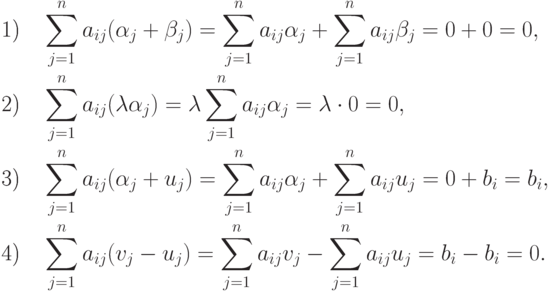
Следствие 4.2.2.
- Множество решений однородной системы
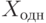 является линейным пространством (подпространством линейного пространства Kn ).
является линейным пространством (подпространством линейного пространства Kn ). - Если
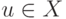 (любое частное решение совместной неоднородной системы), тот. е. множество решений неоднородной системы X является сдвигом подпространства решений однородной системы
(любое частное решение совместной неоднородной системы), тот. е. множество решений неоднородной системы X является сдвигом подпространства решений однородной системы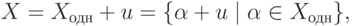
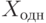 на любое частное решение
на любое частное решение 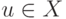 .
.
Доказательство. Если 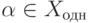 ,
, 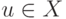 , то в силу 3)
, то в силу 3) 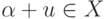 , т. е.
, т. е. 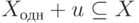 .
.
Если 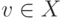 , то v=(v-u)+u, при этом в силу 4)
, то v=(v-u)+u, при этом в силу 4) 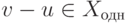 , таким образом,
, таким образом, 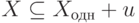 .
.
Итак, X=Xодн+u.
Замечание 4.2.3. Позже мы покажем, что для любого линейного подпространства U линейного пространства строк Kn над полем K существует однородная система линейных уравнений, для которой Xодн=U, таким образом, любое подпространство в Kn может быть задано как пространство решений однородной системы.
