НОУ ИНТУИТ | Введение в алгебру. Лекция 8: Cтупенчатые системы линейных уравнений и метод Гаусса

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5316 / 590 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 68 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Некоторые следствия из метода Гаусса

Следствие 3.7.1. Над полем действительных чисел K= R (и над любым бесконечным полем) число решений системы линейных уравнений может быть равно 0 (несовместная система), 1 (определенная система) и 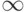$\infty$ (неопределенная система).

Замечание 3.7.2. Над конечным полем Z₂={0,1} из двух элементов система x₁+x₂=0 имеет ровно два решения.

Следствие 3.7.2. (квадратные системы линейных уравнений).

Пусть m=n (т. е. число уравнений равно числу неизвестных). Тогда следующие условия эквивалентны:
а) система определенная (т. е. имеет единственное решение);

б) r=n в ступенчатом виде (т. е. нет свободных неизвестных);

в) соответствующая однородная система имеет только одно решение (0,...,0).
Альтернатива Фредгольма: при m=n либо система линейных уравнений определенная, либо соответствующая ей однородная система имеет ненулевое решение.

Доказательство.

Если в ступенчатом виде r=n, то, учитывая, что m=n, получаем r=n=m. Следовательно, нет "экзотических" уравнений, и поэтому система совместна. Из критерия определенности с этим замечанием получаем, что утверждения а) и б) эквивалентны (и для однородной системы эквивалентны утверждения б) и в)).
С учетом 1) альтернатива Фредгольма соответствует для $r \le n$ следующей альтернативе: либо r=n, либо r<n.

Примеры применения метода Гаусса

$\left\{ \begin{array}{@{}l@{}} x_1-2x_2+x_3+x_4=1,\\ x_1-2x_2+x_3-x_4=-1,\\ x_1-2x_2+x_3+5x_4=5. \end{array} \right.$

$\begin{mult} \left( \begin{matrix} 1 & -2 & 1 & \phm 1\\ 1 & -2 & 1 & -1\\ 1 & -2 & 1 & \phm 5 \end{matrix} \right. \left| \begin{matrix} \phm 1\\ -1\\ \phm 5 \end{matrix} \right) \to{}\\ {}\to \left( \begin{matrix} 1 & -2 & 1 & \phm 1\\ 0 & \phm 0 & 0 & -2\\ 0 & \phm 0 & 0 & \phm 4 \end{matrix} \right. \left| \begin{matrix} \phm 1\\ -2\\ \phm 4 \end{matrix} \right) \to \left( \begin{matrix} 1 & -2 & 1 & \phm 1\\ 0 & \phm 0 & 0 & -2\\ 0 & \phm 0 & 0 & \phm 0 \end{matrix} \right. \left| \begin{matrix} \phm 1\\ -2\\ \phm 0 \end{matrix} \right). \end{mult}$
В ступенчатом виде нет "экзотических" уравнений, следовательно, система совместна. Главные неизвестные - x₁, x₄, свободные неизвестные - x₂, x₃. Если x₂=a, x₃=b, то x₄=1, x₁=1+2a-b-1=2a-b. Таким образом, множество решений имеет вид
$X=\{(2a-b,a,b,1)\mid a,b\in R\}.$
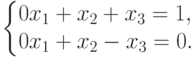$\left\{ \begin{array}{@{}l@{}} 0x_1+x_2+x_3=1,\\ 0x_1+x_2-x_3=0. \end{array} \right.$

$\left( \begin{matrix} 0 & 1 & \phm 1\\ 0 & 1 & -1 \end{matrix} \right. \left| \begin{matrix} 1\\ 0 \end{matrix} \right) \to \left( \begin{matrix} 0 & 1 & \phm 1\\ 0 & 0 & -2 \end{matrix} \right. \left| \begin{matrix} \phm 1\\ -1 \end{matrix} \right).$
Система совместна, главные неизвестные - x₂, x₃, свободная неизвестная - x₁. Ясно, что 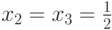$x_2=x_3=\frac{1}{2}$ . Если x₁=a, то множество решений имеет вид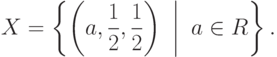
$X=\left\{\left(a,\frac{1}{2},\frac{1}{2}\right) \:\biggm|\: a\in R\right\}.$
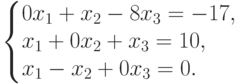$\left\{ \begin{array}{@{}l@{}} 0x_1+x_2-8x_3=-17,\\ x_1+0x_2+x_3=10,\\ x_1-x_2+0x_3=0. \end{array} \right.$

$\begin{mult} \left( \begin{matrix} 0 & \phm 1 & -8\\ 1 & \phm 0 & \phm 1\\ 1 & -1 & \phm 0 \end{matrix} \right. \left| \begin{matrix} -17\\ \phm 10\\ \phm 0 \end{matrix} \right) \to \left( \begin{matrix} 1 & \phm 0 & \phm 1\\ 0 & \phm 1 & -8\\ 1 & -1 & \phm 0 \end{matrix} \right. \left| \begin{matrix} \phm 10\\ -17\\ \phm 0 \end{matrix} \right) \to{}\\ {}\to \left( \begin{matrix} 1 & \phm 0 & \phm 1\\ 0 & \phm 1 & -8\\ 0 & -1 & -1 \end{matrix} \right. \left| \begin{matrix} \phm 10\\ -17\\ -10 \end{matrix} \right) \to \left( \begin{matrix} 1 & 0 & \phm 1\\ 0 & 1 & -8\\ 0 & 0 & -9 \end{matrix} \right. \left| \begin{matrix} \phm 10\\ -17\\ -27 \end{matrix} \right). \end{mult}$
Система совместна (нет "экзотических уравнений"), все неизвестные x₁, x₂, x₃ главные, x₃=3, x₂=7, x₁=7. Система определенная, имеет единственное решение (7,7,3).
$\left\{ \begin{array}{@{}l@{}} x_1+2x_2-3x_3=-2,\\ 3x_1-x_2+2x_3=7,\\ 5x_1+3x_2-4x_3=2. \end{array} \right$ .
$\begin{mult} \left( \begin{matrix} 1 & \phm 2 & -3\\ 3 & -1 & \phm 2\\ 5 & \phm 3 & -4 \end{matrix} \right. \left| \begin{matrix} -2\\ \phm 7\\ \phm 2 \end{matrix} \right) \to \left( \begin{matrix} 1 & \phm 2 & -3\\ 0 & -7 & \phm 11\\ 5 & \phm 3 & -4 \end{matrix} \right. \left| \begin{matrix} -2\\ \phm 13\\ \phm 2 \end{matrix} \right) \to{}\\ {}\to \left( \begin{matrix} 1 & \phm 2 & -3\\ 0 & -7 & \phm 11\\ 0 & -7 & \phm 11 \end{matrix} \right. \left| \begin{matrix} -2\\ \phm 13\\ \phm 12 \end{matrix} \right) \to \left( \begin{matrix} 1 & \phm 2 & -3\\ 0 & -7 & \phm 11\\ 0 & \phm 0 & \phm 0 \end{matrix} \right. \left| \begin{matrix} -2\\ \phm 13\\ -1 \end{matrix} \right). \end{mult}$
Возникло "экзотическое уравнение". Значит, система несовместна.