| Азербайджан |
Классификация на основе байесовской теории решений
2.1. Байесовский подход
Байесовский подход исходит из статистической природы наблюдений. За основу берется предположение о существовании вероятностной меры на пространстве образов, которая либо известна, либо может быть оценена. Цель состоит в разработке такого классификатора, который будет правильно определять наиболее вероятный класс для пробного образа. Тогда задача состоит в определении "наиболее вероятного" класса.
Задано  классов
классов 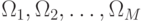 ,
а также
,
а также 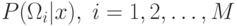 – вероятность того, что
неизвестный образ, представляемый вектором признаков
– вероятность того, что
неизвестный образ, представляемый вектором признаков  , принадлежит
классу
, принадлежит
классу 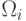 .
.
 называется апостериорной вероятностью, поскольку задает
распределение индекса класса после эксперимента ( a posteriori – т.е.
после того, как значение вектора признаков
называется апостериорной вероятностью, поскольку задает
распределение индекса класса после эксперимента ( a posteriori – т.е.
после того, как значение вектора признаков  было получено).
было получено).
Рассмотрим случай двух классов 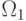 и
и 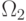 .
Естественно выбрать решающее правило таким образом: объект относим к тому классу, для которого
апостериорная вероятность выше. Такое правило классификации по
максимуму апостериорной вероятности называется Байесовским: если
.
Естественно выбрать решающее правило таким образом: объект относим к тому классу, для которого
апостериорная вероятность выше. Такое правило классификации по
максимуму апостериорной вероятности называется Байесовским: если 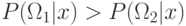 , то
, то  классифицируется в
классифицируется в 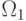 , иначе в
, иначе в 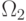 . Таким образом, для Байесовского
решающего правила необходимо получить апостериорные вероятности
. Таким образом, для Байесовского
решающего правила необходимо получить апостериорные вероятности 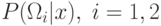 .
Это можно сделать с помощью формулы Байеса.
.
Это можно сделать с помощью формулы Байеса.
Формула Байеса, полученная Т. Байесом, позволяет вычислить апостериорные вероятности событий через априорные вероятности и функции правдоподобия (была опубликована в 1763 году, через два года после смерти автора).
Пусть 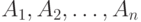 – полная группа несовместных событий.
– полная группа несовместных событий. 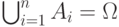 .
. 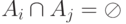 , при
, при 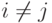 .
Тогда апостериорная вероятность имеет вид:
.
Тогда апостериорная вероятность имеет вид:
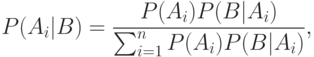
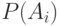 – априорная вероятность события
– априорная вероятность события  – условная вероятность
события
– условная вероятность
события  при условии, что произошло событие
при условии, что произошло событие  .
.Рассмотрим получение апостериорной вероятности  ,
зная
,
зная 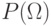 и
и  .
.
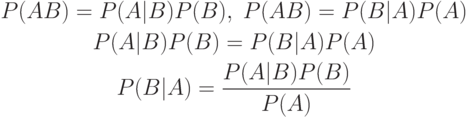
Если 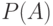 и
и 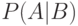 описываются плотностями
описываются плотностями  и
и 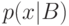 , то
, то
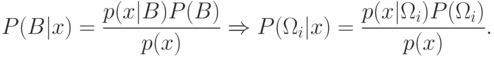
При проверке классификации сравнение 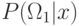 и
и 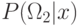 эквивалентно
сравнению
эквивалентно
сравнению 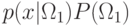 и
и 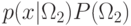 .
В случае, когда
.
В случае, когда  , считается, что мера множества
, считается, что мера множества  равна нулю.
равна нулю.
Таким образом, задача сравнения по апостериорной вероятности
сводится к вычислению величин 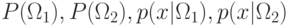 .
Будем считать, что у нас достаточно данных для определения вероятности принадлежности объекта
каждому из классов
.
Будем считать, что у нас достаточно данных для определения вероятности принадлежности объекта
каждому из классов 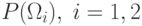 . Такие вероятности называются априорными
вероятностями классов. А также будем считать, что известны функции
распределения вектора признаков для каждого класса
. Такие вероятности называются априорными
вероятностями классов. А также будем считать, что известны функции
распределения вектора признаков для каждого класса 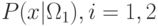 . Они
называются функциями правдоподобия
. Они
называются функциями правдоподобия  по отношению к
по отношению к 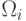 . Если априорные
вероятности и функции правдоподобия неизвестны, то их можно оценить
методами математической статистики на множестве прецедентов. Например,
. Если априорные
вероятности и функции правдоподобия неизвестны, то их можно оценить
методами математической статистики на множестве прецедентов. Например, 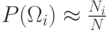 , где
, где 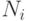 – число прецедентов из
– число прецедентов из 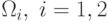 .
.  – общее число прецедентов.
– общее число прецедентов. 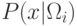 может быть приближено гистограммой распределения вектора признаков
для прецедентов из класса
может быть приближено гистограммой распределения вектора признаков
для прецедентов из класса 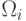 .
.
Итак, Байесовский подход к статистическим задачам основывается на предположении о существовании некоторого распределения вероятностей для каждого параметра. Недостатком этого метода является необходимость постулирования как существования априорного распределения для неизвестного параметра, так и знание его формы.
