| Азербайджан |
Нелинейный классификатор. Многослойный персептрон
5.1. Задача исключающего ИЛИ
Рассмотрим булеву функцию 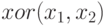 как некий классификатор. Вектор
признаков имеет вид
как некий классификатор. Вектор
признаков имеет вид 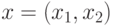 . В данном случае имеется четыре прецедента и два
класса. Напомним таблицу значений функции
. В данном случае имеется четыре прецедента и два
класса. Напомним таблицу значений функции 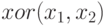 .
.
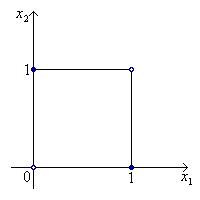
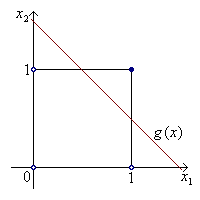
Как видно из рисунка тут нельзя построить разделяющую прямую, поскольку выпуклые оболочки точек, относящихся к первому классу и ко второму классу, пересекаются. Следовательно, и линейный классификатор построить нельзя. Попытаемся построить необходимый нелинейный классификатор как суперпозицию несколько линейных.
Рассмотрим две вспомогательные булевы функции  и
и 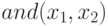 . Напомним
таблицы значений этих функций:
. Напомним
таблицы значений этих функций:
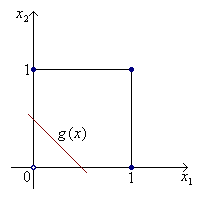
5.1.1. Построение линейного классификатора функции  . Очевидно, что
разделяющей прямой является линия:
. Очевидно, что
разделяющей прямой является линия:

Соответствующий персептрон имеет вид:
5.1.2. Построение линейного классификатора функции 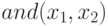 .
Здесь также можно построить разделяющую прямую:
.
Здесь также можно построить разделяющую прямую:
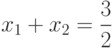
Соответствующий персептрон имеет вид:
5.1.3. Построение нелинейного классификатора функции 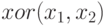 .
Пусть на выходе персептрона для функции
.
Пусть на выходе персептрона для функции  -
- 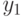 ,
а на выходе персептрона для функции
,
а на выходе персептрона для функции 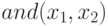 –
– 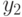 .
Посмотрим, какие значения принимает вектор
.
Посмотрим, какие значения принимает вектор 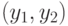 .
.
Обозначив классы как показано в таблице, получаем разделяющую прямую, изображенную на рисунке и соответствующий линейный классификатор:
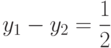
Учитывая вышеизложенное, получаем нелинейный классификатор, который задается через два линейных классификатора, как показано на рисунке слева:
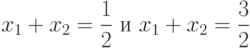
Соответствующий двухслойный персептрон изображен на рисунке справа.